ВИСНОВКИ ДО РОЗДІЛУ 2……………………………………………………….

Дата добавления: 2015-08-30; просмотров: 779

Вид уравнение регрессии в стандартизованном масштабе:

,

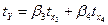где - стандартизованные переменные: , . j = 3, 4.

Одним из способов определения стандартизованных коэффициентов регрессии:

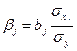, j=3,4.

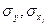- стандартное отклонение, определим из таблицы «Описательная статистика», изображенной на рисунке 5.

;

.

Уравнение регрессии в стандартизованном масштабе примет вид:

,

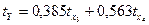Стандартизованные коэффициенты регрессии показывают на сколько «сигм» изменится в среднем результат (У), если соответствующий фактор X_j изменится на одну «сигму» при неизменном среднем уровне других факторов.

В нашем случае показывает, что при увеличении числа орудий поверхностной обработки почв на одну «сигму» урожайность увеличится на 0,385 «сигм», при фиксированном среднем влиянии всех остальных факторов. Аналогичные выводы для .

9. Рассчитайте прогнозное значение результата, если прогнозное значение факторов составляют 80% от их максимальных значений.

Максимальные значения факторов представлены в таблице результатов применения инструмента Описательная статистика, отраженной на рисунке 5. Вектор максимальных значений факторов (х₃; х₄) = (11,51; 1,37).

Определим 80% от Х_max путем умножения каждой координаты вектора на 0,8. Вектор прогнозных значений фактора: (9,208; 1,096).

Подставляя значения Х_р в уравнение регрессии 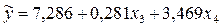получаем 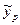=13,675.

10. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости .

Доверительный интервал прогнозного значения функции регрессии определяется по формуле ,

- предельная ошибка прогноза;

табличное значение критерия Стьюдента при уровне значимости α=0,05 и числе степеней свободы v=n-p-1. В нашем случае =2,11.

- стандартная ошибка прогноза,

где S(y) – стандартная ошибка регрессии, определяемая по таблице «ВЫВОД Итогов»;

,

где ∆ - определитель матрицы (Х^ТХ);

А^* - присоединенная матрица или матрица алгебраических дополнений матрицы (Х^ТХ), элементы которой определяются как , |M_ij| - определитель матрицы, получаемый вычеркиванием из (Х^ТХ) i-й строки и j-го столбца.

В ППП Excel Транспонирование матрицы производится следующим образом:

1. в главном меню выберете последовательно пункты Вставка / Функции / Ссылки и массивы / Трансп;

2. заполните диалоговое окно ввода данных:

Массив – диапазон, содержащий элементы матрицы.

Щелкните по кнопке ОК.

3. Выделите диапазон, в котором должны находиться итоги, начиная с ячейки, содержащей формулу. Нажмите F2, а затем Ctrl + Shift + Enter.

Перемножение матриц производится следующим образом:

1. в главном меню выберете последовательно пункты Вставка / Функции / Математические / МУМНОЖ;

2. заполните диалоговое окно ввода данных:

Массив 1 – диапазон, содержащий элементы первой матрицы;

Массив 2 – диапазон, содержащий элементы второй матрицы.

Щелкните по кнопке ОК.

Для получения определителя матрицы (обратной матрицы) необходимо проделать следующие операции:

1. в главном меню выберете последовательно пункты Вставка / Функции / Математические / МОПРЕД (МОБР);

2. заполните диалоговое окно ввода данных:

Массив – диапазон, содержащий элементы матрицы.

Щелкните по кнопке ОК.

Следует помнить, что матрица Х имеет следующий вид: .

Матрица (Х^ТХ) может быть определена с помощью рассмотренных функций транспонирования и умножения матриц, а также элементы матрицы можно рассчитать, исходя из ее общего вида: .

Рассчитаем матрицу . Результаты представим в таблице, изображенной на рисунке 11.

Тогда .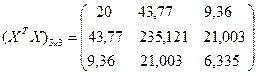

Воспользовавшись функцией нахождения обратной матрицы, результат применения которой представлен на рисунках 12 – 13, получим

.

Рисунок 11- Результаты расчета элементов матрицы (Х^ТХ)

Рисунок 12 – Диалоговое окно функции МОБР

Для (1; 9,208; 1,096) рассчитаем матрицу

= 0,58921.

Порядок и результаты расчетов представлены на рисунке 13.

Стандартная ошибка прогноза: = 2,027.

Для =2,11 предельная ошибка прогноза составит .

Доверительный интервал прогноза: , .

Таким образом, урожайность зерновых культур будет находиться в интервале от 9,398 ц/га до 17, 952 ц/га при числе орудий поверхностной обработки почвы на 100 га 9,2 шт. и 1,096 кг удобрений, расходуемых на гектар, с вероятностью 95%.

Рисунок 13 – Результат вычисления матрицы