Практична робота № 2

Дата добавления: 2015-09-19; просмотров: 638

Основным элементом, из совокупности которых скла­дывается статистическая модель, является одна слу­чайная реализация моделируемого явления, на­пример, «один случай работы машины до ее отказа», «один день работы промышленного цеха», «одна эпи­демия» и т. д. Реализация — это как бы один «экземп­ляр» случайного явления со всеми присущими ему слу­чайностями. Реализации отличаются друг от друга за счет этих случайностей.

Отдельная реализация разыгрывается с помощью специально разработанной процедуры (алгоритма), в которой важную роль играет «бросание жребия». Каж­дый раз, когда в ход явления вмешивается случай, его влияние учитывается не расчетом, а жребием.

Поясним понятие «жребия». Пусть в ходе процесса наступил момент, когда его дальнейшее развитие (а значит и результат) зависит от того, произошло или нет какое-то событие А? Например, попал ли в цель снаряд? Исправна ли аппаратура? Обнаружен ли объ­ект? Устранена ли неисправность? Тогда нужно «бро­санием жребия» решить вопрос: произошло событие или нет. Как можно осуществить этот жребий? Нужно при­вести в действие какой-то механизм случайного выбора (например, бросание монеты или игральной кости, или же вынимание жетона с цифрой из вращающегося ба­рабана, или выбор наугад какого-то числа из таблицы). Нам хорошо знакомы некоторые механизмы случайно­го выбора (например, «пляска шариков» перед объяв­лением выигравших номеров «Спортлото»). Если жре­бий бросается для того, чтобы узнать, произошло ли событие А, его нужно организовать так, чтобы услов­ный результат розыгрыша имел ту же вероятность, что и событие А. Как это делается—мы увидим ниже. Кроме случайных событий, на ход и исход операции могут влиять различные случайные величины, напри­мер: время до первого отказа технического устройства; время обслуживания заявки каналом СМО; размер де­тали; вес поезда, прибывающего на участок пути; ко­ординаты точки попадания снаряда и т. п. С помощью жребия можно разыграть и значение любой случайной величины, и совокупность значений нескольких.

Условимся называть «единичным жребием» любой опыт со случайным исходом, который отвечает на один из следующих вопросов:

1. Произошло или нет событие A?

2. Какое из событий А₁, А₂, ..., A_k произошло?

3. Какое значение приняла случайная величина X?

4. Какую совокупность значений приняла система случайных величин X₁, Х₂, ..., Х_k?

Любая реализация случайного явления методом Монте-Карло строится из цепочки единичных жребиев, перемежающихся с обычными расчетами. Ими учиты­вается влияние исхода жребия на дальнейший ход со­бытий (в частности, на условия, в которых будет ра­зыгран следующий жребий).

Единичный жребий может быть разыгран разными способами, но есть один стандартный механизм, с по­мощью которого можно осуществить любую разновид­ность жребия. А именно, для каждой из них достаточно уметь получать случайное число R, все значения которого от 0 до 1 равновероятны[2]). Условимся крат­ко называть величину R— «случайное число от0до1». Покажем, что с помощью такого числа можно разыг­рать любой из четырех видов единичного жребия.

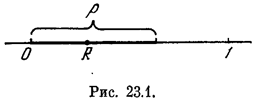
1. Произошло или нет событие А? Чтобы ответить на этот вопрос, надо знать вероятность р события А. Разыграем случайное число R от 0 до 1, и если оно

оказалось меньше р, как

показано на рис. 23.1,

будем считать, что со­бытие произошло, а если больше р — не про­изошло.

А как быть,— спросит читатель,— если число R ока­залось в точности равным р? Вероятностью такого сов­падения можно пренебречь. А уж если оно случилось, можно поступать как угодно: или всякое «равно» счи­тать за «больше», или за «меньше», или попеременно за то и другое — от этого результат моделирования практически не зависит.

2. Какое из нескольких событий появилось? Пусть события А₁, А₂,...,A_k несовместны и образуют пол­ную группу. Тогда сумма их вероятностей р₁, р₂,...,р_k равна единице. Разделим интервал (0, 1) на k участков длиной р₁,р₂,...,р_k (рис. 23.2). На какой из участков попало число R — то событие и появилось.

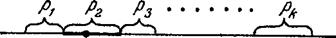
0 R 1

Рис. 23.2.

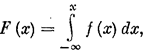Какое значение приняла случайная величина X? Если случайная величина Xдискретна, т. е. имеет зна­чения Х₁, Х₂, . . ., х_k С вероятностями р₁, р₂,...,р_k, ТО, очевидно, случай сводится к предыдущему. Теперь рассмотрим случай, когда случайная величина непре­рывна и имеет заданную плотность вероятности f(x). Чтобы разыграть ее значение, достаточно осуществить следующую процедуру: перейти от плотности вероят­ности f(x) к функции распределения F(x) по формуле

(23.1)

затем найти для функции F обратную ей функцию Ψ.
Затем разыграть случайное число R от 0 до 1 и взять от него эту обратную функцию:

X= Ψ(R). (23.2)

Можно доказать (мы этого делать не будем), что полученное значение X имеет как раз нужное нам распределение f(x).

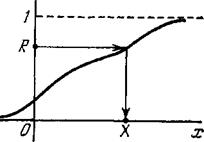Графически процедура розыгрыша значения X показана на рис. 23.3. Разыгрывается число R от 0 до 1 и для него ищется такое значение X, при котором F(X) = R

*= R (это показано стрелками
на рис. 23.3).

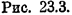На практике часто приходится разыгрывать значение случайной величины, имеющей нормальное распределение. Для нее, как для любой непрерывной случайной величины, правило розыгрыша (23.2) остается справедливым, но

можно поступать и иначе (проще). Известно, что (согласно центральной предельной тео­реме теории вероятностей) при сложении достаточно большого числа независимых случайных величин с одинаковыми распределениями получается случайная величина, имеющая приближенно нормальное распре­деление. На практике, чтобы получить нормальное рас­пределение, достаточно сложить шесть экземпляров случайного числа от 0 до 1. Сумма этих шести чисел

Z = R1 +R2 + ... + Rв (23.3)

имеет распределение, настолько близкое к нормально­му, что в большинстве практических задач им можно заменить нормальное. Для того чтобы математическое ожидание и среднее квадратическое отклонение этого нормального распределения были равны заданным т_х, _х, нужно подвергнуть величину Z линейному преобра­зованию и вычислить

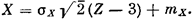(23.4)

Это и будет нужная нам нормально распределенная случайная величина.

1. Какую совокупность значений приняли случай­ные величины Х₁Х₂,...,Х_k? Если случайные величины независимы, то достаточно k раз повторить процедуру, описанную в предыдущем пункте. Если же они зави­симы, то разыгрывать каждую последующую нужно на основе ее условного закона распределения при условии, что все предыдущие приняли те значения, которые дал розыгрыш (более подробно останавливать­ся на этом случае мы не будем).

Таким образом, мы рассмотрели все четыре варианта единичного жребия и убедились, что все они сво­дятся к розыгрышу (одно- или многократному) слу­чайного числа R от 0 до 1.

Возникает вопрос: а как же разыгрывается это чис­ло R? Существует целый ряд разновидностей так на­зываемых «датчиков случайных чисел», решающих эту задачу. Остановимся вкратце на некоторых из них.

Самый простой из датчиков случайных чисел — это вращающийся барабан, в котором перемешиваются перенумерованные шарики (или жетоны). Пусть, на­пример, нам надо разыграть случайное число R от 0 до 1 c точностью до 0,001. Заложим в барабан 1000 пере­нумерованных шариков, приведем его во вращение и после остановки выберем первый попавшийся шарик, прочтем его номер и разделим на 1000.

Можно поступить и немного иначе: вместо 1000 шариков заложить в барабан только 10, с цифрами 0, 1, 2, ...,9. Вынув один шарик, прочтем первый деся­тичный знак дроби. Вернем его обратно, снова покру­тим барабан и возьмем второй шарик — это будет второй десятичный знак и т. д. Легко доказать (мы этого делать не будем), что полученная таким образом десятичная дробь будет иметь равномерное распреде­ление от 0 до 1. Преимущество этого способа в том, что он никак не связан с числом знаков, с которым мы хотим знать R.

Отсюда один шаг до рационализаторского предло­жения: не разыгрывать число R каждый раз, когда это понадобится, а сделать это заранее, т. е. составить достаточно обширную таблицу, в которой все цифры 0, 1, 2, ..9 встречаются случайным образом и с оди­наковой вероятностью (частотой). До этого приема люди давно додумались: такие таблицы действительно со­ставлены и применяются на практике. Они называют­ся таблицами случайных чисел. Выдержки из таблиц случайных чисел приводятся во многих ру­ководствах по теории вероятностей и математической статистике (например, [20]). Краткие выдержки из таблиц случайных чисел приведены и в популярной книжке автора [21], где, кстати, даны и примеры мо­делирования случайных процессов с помощью таблиц случайных чисел.

При ручном применении метода Монте-Карло таб­лицы случайных чисел — наилучший способ розыгры­ша случайного числа R от 0 до 1. Если же моделирова­ние осуществляется не вручную, а на ЭВМ, то поль­зование таблицами случайных чисел (как и вообще таблицами) нерационально — они слишком загрузили бы память. Для розыгрыша R на ЭВМ применяются специальные датчики, которыми оснащены многие вычислительные машины. Это могут быть как «физиче­ские датчики», основанные на преобразовании случай­ных шумов, так и вычислительные алгоритмы, по кото­рым сама машина вычисляет так называемые «псев­дослучайные числа». Приставка «псевдо» означает «как бы», «якобы». И в самом деле, числа, вычисляе­мые с помощью таких алгоритмов, фактически случай­ными не являются, но практически ведут себя как случайные; все значения от 0 до 1 встречаются в сред­нем одинаково часто и, кроме того, связь между пос­ледовательными значениями получаемых чисел прак­тически отсутствует. Существует ряд алгоритмов вычис­ления псевдослучайных чисел, различающихся между собой по простоте, равномерности и другим признакам (см. [22]). Один из самых простых алгоритмов вычис­ления псевдослучайных чисел состоит в следующем. Берут два произвольных n-значных двоичных числа а₁ и а₂, перемножают их и в полученном произведении берут п средних знаков; это будет число а₃. Затем пе­ремножают а₂ и а₃, в произведении снова берут n средних знаков и т. д. Полученные таким образом числа рассматривают как последовательность двоичных дро­бей с п знаками после запятой. Такая последователь­ность дробей ведет себя практически как ряд значений случайного числа R от 0 до 1. Существуют и другие алгоритмы, основанные не на перемножении, а на «суммировании со сдвигом». Подробнее останавливаться на конкретных алгоритмах получения псевдослучайных чисел не имеет смысла: в настоящее время прак­тически все ЭВМ cнабжены либо датчиками случай­ных чисел, либо проверенными алгоритмами вычисле­ния псевдослучайных[3]).

§ 24. Определение характеристик стационарного случайного процесса по одной реализации

В исследовании операций нередко приходится встречаться с задачами, где случайный процесс про­должается достаточно долго в одинаковых условиях, и нас как раз интересуют характеристики этого процес­са в предельном, установившемся режиме. Например, железнодорожная сортировочная станция работает круглосуточно, и интенсивность потока составов, при­бывающих на нее, почти не зависит от времени. В ка­честве других примеров систем, в которых случайный процесс довольно быстро переходит в устойчивое состо­яние, можно назвать ЭВМ, линии связи, технические устройства, непрерывно эксплуатируемые и т. п.

О предельном, стационарном режиме и предельных (финальных) вероятностях состояний мы уже говори­ли в главе 5 (§ 17) в связи с марковскими случайными процессами. Существуют ли они для немарковских процессов? Да, в известных случаях существуют и не зависят от начальных условий. При решении вопроса о том, существуют ли они для данной задачи, можно в первом приближении поступать так: заменить мыс­ленно все потоки событий простейшими; если для этого случая окажется, что финальные вероятности сущест­вуют, то они будут существовать и для немарковского процесса. Если это так, то для предельного, стацио­нарного режима все вероятностные характеристики можно определить методом Монте-Карло не по мно­жеству реализаций, а всего по одной, но достаточно длинной реализации. В этом случае одна длинная реа­лизация дает такую же информацию о свойствах процесса, что и множество реализаций той же общей продолжительности.

Пусть в нашем распоряжении — одна длинная реализация стационарного случайного процесса общей продолжительности Т. Тогда интересующие нас вероятности состояний можно найти, как долю

времени, которую система проводит в этих состояниях, а средние значения случайных величин получить усреднением не по множеству реализаций, а по времени, вдоль реализации.

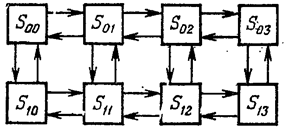
Рассмотрим пример. Моделируется методом Монте- Карло работа немарковской одноканальной СМО с оче­редью. Число мест в очереди ограничено двумя. Заяв­ка, пришедшая в момент, когда оба места в очереди заняты, покидает СМО необслуженной (получает от­каз). Время от времени канал может выходить из строя. Если канал вышел из строя, находившиеся в СМО заявки (как под обслуживанием, так и в очере­ди), не покидают СМО, а ожидают конца ремонта. Все потоки событий не простейшие, а произвольные рекур­рентные. Возможные состояния СМО:

S_oi — канал исправлен, в системе i заявок,

S_1i — канал ремонтируется, в системе i заявок (i = 0, 1, 2, 3).

Граф состояний СМО показан на рис. 24.1. Из ви­да графа заключаем, что финальные вероятности су­ществуют. Предположим, что моделирование работы СМО методом Монте-Карло на большом промежутке времени Т произведено. Требуется найти характери­стики эффективности СМО: Р_oтк — вероятность того, что заявка покинет СМО необслуженной, Р_испр — веро­ятность того, что канал исправен, А — абсолютную пропускную способность СМО, L_сист — среднее число заявок в СМО, L_оч — среднее число заявок в очереди, W_сист и W_оч — среднее время пребывания заявки в си­стеме и в очереди.

Сначала найдем финальные вероятности состояний p₀₀, p₀₁, p₀₂, p₀₃, p₁₀, p₁₁, p₁₂, p₁₃. Для этого нужно вдоль реализации подсчитать суммарное время, которое си­стема находится в каждом из состояний: T₀₀, T₀₁, T₀₂, T₀₃, Т₁₀, T₁₁, Т12, T₁₃, и разделить каждое из них на время Т. Получим:

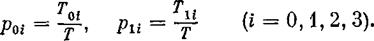
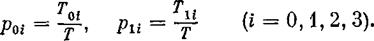
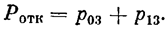Вероятность отказа равна вероятности того, что за­явка придет в момент, когда в СМО уже находятся три заявки:

Абсолютная пропускная способность равна

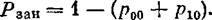
где λ — интенсивность потока заявок.

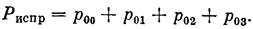Вероятность того, что канал исправен, получим, суммируя все вероятности, у которых первый индекс равен нулю:

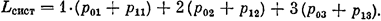Среднее число заявок в СМО подсчитаем, умножая возможные числа заявок в СМО на соответствующие вероятности и складывая:

Это равносильно тому, как если бы мы отметили на оси времени отрезки, на которых в СМО находится 0, 1, 2, 3 заявки и суммарную длительность участков умножили соответственно на 1, 2, 3, сложили и раз­делили на T.

Среднее число заявок в очереди L_oч получим, вычи­тая из L_сист среднее число заявок под обслуживанием (для одноканальной СМО это вероятность того, что канал занят):

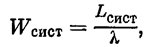
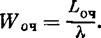
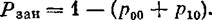
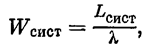Среднее время пребывания заявки в системе и в очереди получим по формуле Литтла:

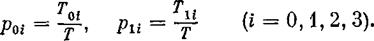
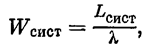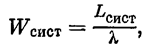
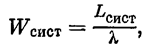
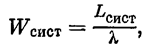
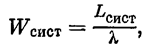
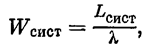
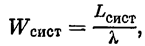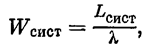На этом мы заканчиваем краткое изложение метода Монте-Карло, отсылая интересующегося читателя к руководствам [6,22], где он изложен более полно и где, в частности, рассматривается вопрос о точности стати­стического моделирования.

ГЛАВА 8