
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Мета роботи
Дата добавления: 2015-09-19; просмотров: 697
|
|
Самым простым случаем, подробно разработанным в теории игр, является конечная парная игра с нулевой суммой (антагонистическая игра двух лиц или двух коалиций). Рассмотрим такую игру G, в которой участвуют два игрока А и В, имеющие противоположные интересы: выигрыш одного равен проигрышу другого. Так как выигрыш игрока А равен выигрышу игрока В с обратным знаком, мы можем интересоваться только выигрышем а игрока А. Естественно, А хочет максимизировать, а В — минимизировать а. Для простоты отождествим себя мысленно с одним из игроков (пусть это будет А) и будем его называть «мы», а игрока В — «противник» (разумеется, никаких реальных преимуществ для А из этого не вытекает). Пусть у нас имеется т возможных стратегий А1 А2, ... Аm, а у противника — п возможных стратегий В1, В2, ..., Вп (такая игра называется игрой тхп). Обозначим аij наш выигрыш в случае, если мы пользуемся стратегией а противник — стратегией
Т а б л и ц а 26.1
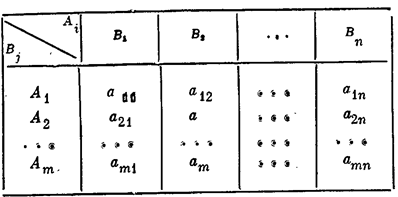
Bj. Предположим, что для каждой пары стратегий Аi, Вj выигрыш (или средний выигрыш) aij нам известен. Тогда в принципе можно составить прямоугольную таблицу (матрицу), в которой перечислены стратегии игроков и соответствующие выигрыши (см. таблицу 26.1).
Если такая таблица составлена, то говорят, что игра G приведена к матричной форме (само по себе приведение игры к такой форме уже может составить трудную задачу, а иногда и практически невыполнимую, из-за необозримого множества стратегий). Заметим, что если игра приведена к матричной форме, то многоходовая игра фактически сведена к одноходовой — от игрока требуется сделать только один ход: выбрать стратегию. Будем кратко обозначать матрицу игры (aij).
Рассмотрим пример игры G (4X5) в матричной форме. В нашем распоряжении (на выбор) четыре стратегии, у противника — пять стратегий. Матрица игры дана в таблице 26.2
Давайте, поразмышляем о том, какой стратегией нам (игроку А) воспользоваться? В матрице 26.2 есть соблазнительный выигрыш «10»; нас так и тянет выбрать стратегию A3, при которой этот «лакомый кусок» нам достанется. Но постойте: противник тоже не дурак! Если мы выберем стратегию A3, он, назло нам, выберет стратегию B3, и мы получим какой-то жалкий выигрыш «1». Нет, выбирать стратегию Л3 нельзя! Как же быть? Очевидно, исходя из принципа осторожности (а он — основной принцип теории игр), надо выбрать
Таблица 26.2
| В} | в, | в2 | я3 | в4 | вь |
| А1 | |||||
| а2 | |||||
| А з | |||||
| А 4 |
ту стратегию, при которой наш минимальный выигрыш максимален. Это — так называемый «принцип мини- макса»: поступай так, чтобы при наихудшем для тебя поведении противника получить максимальный выигрыш.
Перепишем таблицу 26.2 и в правом добавочном столбце запишем минимальное значение выигрыша в каждой строке (минимум строки); обозначим его для i-й строки аi (см. таблицу 26.3).
Таблица 26.3
| А. * , | в, | в, | вз | в< | в6 | а. г |
| А\ | ||||||
| А 2 | ||||||
| А з | ||||||
| А 4 | ||||||
| р, |
Из всех значений ai (правый столбец) выделено наибольшее (3). Ему соответствует стратегия A4. Выбрав эту стратегию, мы во всяком случае можем, быть уверены, что (при любом поведении противника) выиграем не меньше, чем 3. Эта величина — наш гарантированный выигрыш; ведя себя осторожно, меньше этого мы получить не можем (а, может быть, получим и больше). Этот выигрыш называется нижней ценой игры (или «максимином» — максимальный из минимальных выигрышей). Будем обозначать его а. В нашем случае α = 3.
Теперь станем на точку зрения противника и порассуждаем за него. Он ведь не пешка какая-нибудь, а тоже разумен! Выбирая стратегию, он хотел бы отдать поменьше, но должен рассчитывать на наше, наихудшее для него, поведение. Если он выберет стратегию В1, мы ему ответим A3, и он отдаст 10; если выберет B2 — мы ему ответим А2, и он отдаст 8 и т. д. Припишем к таблице 26.3 добавочную нижнюю строку и в ней запишем максимумы столбцов βj. Очевидно, осторожный противник должен выбрать ту стратегию, при которой эта величина минимальна (соответствующее значение 5 выделено в таблице 26.3). Эта величина β — то значение выигрыша, больше которого заведомо не отдаст нам разумный противник. Она называется верхней ценой игры (или «минимаксом» — минимальный из максимальных выигрышей). В нашем примере β = 5 и достигается при стратегии противника Bз.
Итак, исходя из принципа осторожности (перестраховочного правила «всегда рассчитывай на худшее!»), мы должны выбрать стратегию а противник — стратегию A4, а противник — стратегию Bз. Такие стратегии называются «минимаксными» (вытекающими из принципа минимакса). До тех пор, пока обе стороны в нашем примере будут придерживаться своих минимаксных стратегий, выигрыш будет равен α 4з = 3.
Теперь представим себе на минуту, что мы узнали о том, что противник придерживается стратегии Bз.
А ну-ка, накажем его за это и выберем стратегию A1- мы получим 5, а это не так уж плохо. Но ведь противник— тоже не промах; пусть он узнал, что наша стратегия А1 он тоже поторопится выбрать В4, сведя наш выигрыш к 2, и т. д. (партнеры «заметались по стратегиям»). Одним словом, минимаксные стратегии в нашем примере неустойчивы по отношению к информации о поведении другой стороны; эти стратегии не обладают свойством равновесия. 4
Всегда ли это так? Нет, не всегда. Рассмотрим пример с матрицей, данной в таблице 26.4
В этом примере нижняя цена игры равна верхней: а = β = 6. Что из этого вытекает? Минимаксные стратегии игроков. А и В будут устойчивыми. Пока оба игрока их придерживаются, выигрыш равен 6. Посмотрим, что будет, если мы (А) узнаем, что противник (В)
| Таблица 26.4 |
| Таблица 26.4 |

 держится стратегии В2? А ровно ничего не изменится, Потому что любое отступление от стратегии А2 может только ухудшить наше положение. Равным образом, информация, полученная противником, не заставит его отступить от своей стратегии В2. Пара стратегий А2, В2 обладает свойством равновесия (уравновешенная пара стратегий), а выигрыш (в нашем случае 6), достигаемый при этой паре стратегий, называется «седловой точкой матрицы» [4]). Признак наличия седловой точки и уравновешенной пары стратегий — это равенство нижней и верхней цены игры; общее значение аир называется ценой игры. Мы будем обозначать его v:
держится стратегии В2? А ровно ничего не изменится, Потому что любое отступление от стратегии А2 может только ухудшить наше положение. Равным образом, информация, полученная противником, не заставит его отступить от своей стратегии В2. Пара стратегий А2, В2 обладает свойством равновесия (уравновешенная пара стратегий), а выигрыш (в нашем случае 6), достигаемый при этой паре стратегий, называется «седловой точкой матрицы» [4]). Признак наличия седловой точки и уравновешенной пары стратегий — это равенство нижней и верхней цены игры; общее значение аир называется ценой игры. Мы будем обозначать его v:
(26.1)
Стратегии Ai, Bj (в данном случае А2, В2), при которых этот выигрыш достигается, называются оптимальными чистыми стратегиями, а их совокупность — решением игры. Про саму игру в этом случае говорят, что она решается в чистых стратегиях. Обеим сторонам А и В можно указать их оптимальные стратегии, при которых их положение — наилучшее из возможных. А что игрок А при этом выигрывает 6, а игрок В — проигрывает 6,— что же, таковы условия игры: они выгодны для А и невыгодны для В.
У читателя может возникнуть вопрос: а почему оптимальные стратегии называются «чистыми»? Несколько забегая вперед, ответим на этот вопрос: бывают стратегии «смешанные», состоящие в том, что игрок применяет не одну какую-то стратегию, а несколько, перемежая их случайным образом. Так вот, если допустить кроме чистых еще и смешанные стратегии, всякая конечная игра имеет решение — точку равновесия. Но об этом речь еще впереди.
Наличие седловой точки в игре — это далеко не правило, скорее — исключение. Большинство игр не имеет седловой точки. Впрочем, есть разновидность игр, которые всегда имеют седловую точку и, значит, решаются в чистых стратегиях. Это — так называемые «игры с полной информацией». Игрой с полкой информацией называется такая игра, в которой каждый игрок при каждом личном ходе знает всю предысторию ее развития, т. е. результаты всех предыдущих ходов, как личных, так и случайных. Примерами игр с полной информацией могут служить: шашки, шахматы, «крестики и нолики» и т. п.
В теории игр доказывается, что каждая игра с полной информацией имеет седловую точку, и значит, решается в чистых стратегиях. В каждой игре с полной информацией существует пара оптимальных стратегий, дающая устойчивый выигрыш, равный цене игры v. Если такая игра состоит только из личных ходов, то при применении каждым игроком своей оптимальной стратегии она должна кончаться вполне определенным образом — выигрышем, равным цене игры. А значит, если решение игры известно, самая игра теряет смысл!
Возьмем элементарный пример игры с полной информацией: два игрока попеременно кладут пятаки на круглый стол, выбирая произвольно положение центра монеты (взаимное перекрытие монет не разрешается). Выигрывает тот, кто положит последний пятак (когда места для других уже не останется). Легко убедиться, что исход этой игры, в сущности, предрешен. Есть определенная стратегия, обеспечивающая выигрыш тому из игроков, кто кладет монету первым. А именно, он должен первый раз положить пятак в центре стола, а затем на каждый ход противника отвечать симметричным ходом. Очевидно, как бы ни вел себя противник, ему не избежать проигрыша. Точно так же обстоит дело и с шахматами и вообще играми с полной информацией: любая из них, записанная в матричной форме, имеет седловую точку, и значит, решение в чистых стратегиях, а следовательно, имеет смысл только до тех пор, пока это решение не найдено. Скажем, шахматная игра либо всегда кончается выигрышем белых, либо всегда — выигрышем черных, либо всегда — ничьей, только чем именно — мы пока не знаем (к счастью для любителей шахмат). Прибавим еще: вряд ли будем знать и в обозримом будущем, ибо число стратегий так огромно, что крайне трудно (если не невозможно) привести игру к матричной форме и найти в ней седловую точку.
А теперь спросим себя, как быть, если игра не имеет седловой точки: α≠β? Ну что же, если каждый игрок вынужден выбрать одну-единственную чистую стратегию, то делать нечего: надо руководствоваться принципом минимакса. Другое дело, если можно свои стратегии «смешивать», чередовать случайным образом с какими-то вероятностями. Применение смешанных стратегий мыслится таким образом: игра повторяется много раз; перед каждой партией игры, когда игроку предоставляется личный ход, он «передоверяет» свой выбор случайности, «бросает жребий», и берет ту стратегию, которая выпала (как организовать жребий, мы уже знаем из предыдущей главы).
Смешанные стратегии в теории игр представляют собой модель изменчивой, гибкой тактики, когда ни один из игроков не знает, как поведет себя противник в данной партии. Такая тактика (правда, обычно безо всяких математических обоснований) часто применяется в карточных играх. Заметим при этом, что лучший способ скрыть от противника свое поведение — это придать ему случайный характер и, значит, самому не знать заранее, как ты поступишь.
Итак, поговорим о смешанных стратегиях. Будем обозначать смешанные стратегии игроков А и В соответственно SA = (p1, p2 , ...,pm), SB = (q1, q2, …, qn), где p1, р2, ..., рт (образующие в сумме единицу) — вероятности применения игроком А стратегий А1, A2, ..., Ат; q1, q2, …, qn — вероятности применения игроком В стратегий В1, В2 ,…,Вп. В частном случае, когда все вероятности, кроме одной, равны нулю, а эта одна — единице, смешанная стратегия превращается в чистую.
Существует основная теорема теории игр: любая конечная игра двух лиц с нулевой суммой имеет по крайней мере одно решение — пару оптимальных стратегий, в общем случае смешанных (S*A, S*B), и соответствующую цену v.
Пара оптимальных стратегий (S*A S*B). образующих решение игры, обладает следующим свойством: если один из игроков придерживается своей оптимальной, стратегии, то другому не может быть выгодно отступать от своей. Эта пара стратегий образует в игре некое положение равновесия: один игрок хочет обратить выигрыш в максимум, другой — в минимум, каждый тянет в свою сторону и, при разумном поведении обоих, устанавливается равновесие и устойчивый выигрыш v. Если v> 0, то игра выгодна для нас, если v < 0 — для противника; при v= 0 игра «справедливая», одинаково выгодная для обоих участников.
Рассмотрим пример игры без седловой точки и приведем (без доказательства) ее решение. Игра состоит в следующем: два игрока А и В одновременно и не сговариваясь показывают один, два или три пальца. Выигрыш решает общее количество пальцев: если оно четное, выигрывает А и получает у В сумму, равную этому числу; если нечетное, то, наоборот, А платит В сумму, равную этому числу. Как поступать игрокам?
Составим матрицу игры. В одной партии у каждого игрока три стратегии: показать один, два или три пальца. Матрица 3x3 дана в таблице 26.5; в дополнительном правом столбце приведены минимумы строк, а в дополнительной нижней строке — максимумы столбцов.
Нижняя цена игры α = —3 и соответствует стратегии А1. Это значит, что при разумном, осторожном поведении, мы гарантируем, что не проиграем больше, чем 3. Слабое утешение,, но все же лучше, чем, скажем, выигрыш —5, встречающийся в некоторых клетках матрицы. Плохо нам, игроку А... Но утешимся: положение противника, кажется, еще хуже: .нижняя цена игры β=4, т. е. при разумном поведении он отдаст нам минимум 4. В общем, положение не слишком хорошее — ни для той, ни для другой стороны. Но посмотрим: нельзя ли его улучшить? Оказывается, можно. Если каждая сторона будет применять не одну какую-то чистую стратегию, а смешанную, в которую
Таблица 26.5

первая и третья входят с вероятностями 1/4, а вторая — с вероятностью 1/2, т. е.

то средний выигрыш будет устойчиво равен нулю (значит, игра «справедлива» и одинаково выгодна той и другой стороне). Стратегии S*A, S*B образуют решение игры, а ее цена v = 0. Как мы это решение нашли? Это вопрос другой. В следующем параграфе мы покажем, как вообще решаются конечные игры.
| <== предыдущая лекция | | | следующая лекция ==> |
| Мета роботи | | | Нейрон як об’єкт Психофізіології. Структурно функціональні особливості нейрону. |