Задача № 1.

Дата добавления: 2015-09-19; просмотров: 481

History shows the necessity for the invention of new numbers in the orderly progress of civilization and in the evolution of maths. We must review briefly the growth of the number system in the light of the theory of equations and see why the complex number system need not be enlarged fur­ther. Suppose we decide that we want all polynomial equations to have roots. Now let us imagine that we have no numbers in our possession except the natural numbers. Then a simple linear equation like 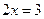has no root. In order to remedy this condition, we invent fractions. But a simple linear equa­tion, like has no root even among the fractions. Hence we invent negative numbers. A simple quadratic equation like has no root among all the (positive and negative) rational numbers, therefore we invent the irra­tional numbers which together with the rational numbers complete the sys­tem of real numbers.

However, a simple quadratic equation like 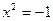has no root among all the real numbers, hence, we invent the pure imaginary numbers. But a simple quadratic equation like 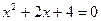has no roots among either the real or pure imaginary numbers; therefore we invent the complex numbers. The story of , the imaginary unit, and of , the complex number, originated in the logical development of algebraic theory. The word "imaginary" reflects the elusive nature of the concept for distinguished mathematicians who lived centuries ago. Early consideration of the square root of a negative number brought unvarying rejection. It seemed obvious that a negative num­ber is not a square, and hence it was concluded that such square roots had no meaning. This attitude prevailed for a long time.

G. Cardano (1545) is credited with some progress in introducing complex numbers in his solution of the cubic equation, even though he regarded them as "fictitious". He is credited also with the first use of the square root of a negative number in solving the now-famous problem, "Divide 10 into two parts such that the product... is 40", which Cardano first says is "manifest­ly impossible"; but then he goes on to say, in a properly adventurous spirit, "Nevertheless, we will operate." Thus he found and and showed that they did, indeed, have the sum of 10 and a product of 40. Cardano concludes by saying that these quantities are "truly sophisticat­ed" and that to continue working with them is "as subtle as it is useless". Cardano did not use the symbol , his designation was " ", that is, "radix minus", for the square root of a negative number. R. Descartes (1637) contributed the terms "real" and "imaginary". L. Euler (1748) used "i" for and K. F. Gauss (1832) introduced the term "complex number". He made significant contributions to the understanding of complex numbers through graphical representation and defined complex numbers as ordered pairs of real numbers for which

,

and so forth.

Now, we may well expect that there may be some equation of degree 3 or higher which has no roots even in the entire system of complex num­bers. That this is not the case was known to K. F. Gauss, who proved in 1799 the following theorem, the truth of which had long been expected: Every algebraic equation of degree n withcoefficient in the complex number system has a root (and hence n roots) among the complex numbers, later Gauss published three more proofs of the theorem. It was he who called it "fundamental theorem of algebra". Much of the work on complex number theory is Gauss'. He was one of the first to represent complex numbers as points in a plane. Actually, Gauss gave four proofs for the theorem, the last when he was seventy; in the first three proofs, he assumes, the coefficients of the polynomial equation are real, but in the fourth proof the coefficients are any complex numbers. We can be sure now that for the purpose of solv­ing polynomial equations we do not need to extend the number system any further.