Заняття 3.

Дата добавления: 2015-09-19; просмотров: 543

1. Review the whole text again. Outline the subject matter of the text, its components structure, topic sentences and main ideas. Use the following phrases:

– The text deals with … (speaks about, presents, shows, points out, discusses, reviews, throws light on, traces the history of, etc)

– The subject matter of the text is …

– The text can be segmented into … paragraphs.

– The first (second, third, fourth, etc.) paragraph considers … (deals with, informs of, describes, etc.)

– The topic sentence of the first (second, third, fourth, etc.) paragraph is …

– The main idea of the first (second, third, fourth, etc.) paragraph is …

– The main idea of the text is …

– The conclusion the author came to is …

– The reasons for this conclusion are …

2. Say whether the following statements are true or false. Justify your choice. Use the given phrases:

That’s right…

Exactly. Quite so…

I fully agree to it…

I don’t think this is the case…

Quite the contrary…

Not quite. It’s unlikely…

Just the reverse…

1. The rational numbers complete the system of real numbers.

2. A simple quadratic equation like 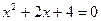has no roots among either the real or pure imaginary numbers.

3. Early consideration of the square root of a negative number was crowned with success.

4. An equation has as many roots as its degree.

5. No general algebraic solution is possible for the polynomial equation of degree greater than four.

6. In algebra x always stands for number.

7. A complex number is essentially a pair of real numbers .

8. L.Euler introduced the term “complex number”.

9. Gauss gave the last proof for the theorem when he was seventy.

10. For the purpose of solving polynomial equations we need to extend the number system further.

3. Answer the following questions:

1. Is there any necessity for the invention of new numbers in the evolution of math?

2. Why were fractions invented?

3. Why were negative numbers, rational numbers and irrational numbers invented?

4. What numbers complete the system of real numbers?

5. Does a simple quadratic equation like have no root among all real numbers?

6. What caused the invention of the pure imaginary numbers and the complex numbers?

7. What does the word “imaginary” reflect?

8. Why did early consideration of the square root of a negative number bring unvarying rejection?

9. What is G.Cardano credited with?

10. Who contributed the terms “real” and “imaginary”?

11. Who introduced the term “complex number”?

12. What theorem did K.F.Gauss prove in 1799?

13. How many proofs of this theorem are there?

14. What theorem is called “fundamental theorem of algebra”?

15. Do they need to extend the number system further?

4. For each definition choose a term from the left column:

the complex number	is any real number that cannot be expressed as a ratio , where and are integers, with non-zero, and is therefore not a rational number.
the natural number	a statement of the equality between mathematical expressions.
fraction	a number which can be put in the form , where and are real numbers and 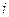is called the imaginary unit, where .
the rational numbers	a noninteger quantity expressed in terms of a numerator and a denomerator or in decimal form.
the irrational numbers	the limit of a convergent sequence of rational numbers.
the system of real number	a number that can be expressed as a fraction where and are integers and .
equation	a positive integer.