Дубильні речовини

Дата добавления: 2015-10-12; просмотров: 507

Рассмотрим функцию , где .

Определение 1.Функцию, аргументом которой служит натуральное число n, называют числовой последовательностью.

Значения функции называются членами или элементами этой последовательности и обозначаются, как правило,

, так что , ,…, .

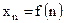Сокращенно последовательность обозначается символом . Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности.

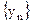Суммой, разностью, произведением и частным последовательностей и называются соответственно последовательности

, , …, ,…,

, , …, ,…,

, , …, , … .

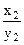Символически вышеуказанные действия записываются следующим образом:

, , .

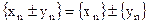Заметим, что значения членов последовательности не должны быть обязательно различными. Например, если , , , то соответствующие последовательности имеют вид

; ; .

В первом случае имеем просто постоянную величину, во втором члены последовательности принимают два различных значения, в третьем множество значений переменной бесконечно.

Определение 2.Последовательность назовем ограниченной сверху (снизу), если существует такое число ( ), что любой элемент этой последовательности удовлетворяет неравенству ( ).

Последовательность называется ограниченной, если она ограничена и снизу, и сверху, то есть существуют такие числа и , что для любого : . Обозначим . Тогда условие ограниченности можно записать в виде .

Например, последовательность ограничена снизу, но не ограничена сверху;

последовательность ограничена сверху, но не ограничена снизу;

последовательность ограничена, так как любой элемент этой последовательности удовлетворяет неравенству .