
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Вітаміни
Дата добавления: 2015-10-12; просмотров: 520
|
|
Определение 1.Число a называется пределом последовательности  , если для любого положительного
, если для любого положительного  , сколь бы мало оно ни было, существует такой номер
, сколь бы мало оно ни было, существует такой номер  , что для всех
, что для всех 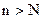 выполняется неравенство
выполняется неравенство
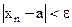 . (2.1)
. (2.1)
Тот факт, что a является пределом последовательности  , записывают так:
, записывают так:
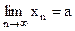 или
или  . (2.2)
. (2.2)
Если предел последовательности существует, то говорят также, что последовательность  сходится.
сходится.
Заметим, что номер N зависит от выбора  , то есть
, то есть 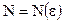 .
.
Используя логические символы, это определение можно записать следующим образом:
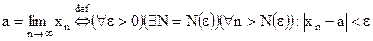 .
.
Если изобразить числа  ,
,  ,
, 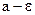 и значения
и значения  точками числовой оси, то получится геометрическая интерпретация предела последовательности (рис).
точками числовой оси, то получится геометрическая интерпретация предела последовательности (рис).
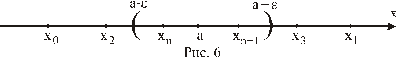
Какой бы малый промежуток длины  с центром в точке a ни взять, все точки
с центром в точке a ни взять, все точки  , начиная с некоторой из них, должны попасть внутрь этого промежутка. Особый интерес вызывает случай, когда
, начиная с некоторой из них, должны попасть внутрь этого промежутка. Особый интерес вызывает случай, когда  , который рассмотрим позднее.
, который рассмотрим позднее.
Рассмотрим некоторые свойства сходящихся последовательностей, сформулировав их в виде теорем.
Теорема 1. Если последовательность  имеет предел, равный a, и
имеет предел, равный a, и 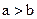
 , то и члены последовательности
, то и члены последовательности 
 , начиная с некоторого номера.
, начиная с некоторого номера.
■ Пусть 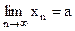 и
и 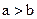 . Подберем число
. Подберем число  так, чтобы
так, чтобы 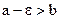 ; для этого достаточно взять
; для этого достаточно взять  . Но тогда по определению предела найдется такой номер N, что для
. Но тогда по определению предела найдется такой номер N, что для 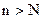 выполняется
выполняется  , а, следовательно, тем более
, а, следовательно, тем более  . ■
. ■
Теорема 2. Если  и
и 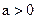
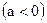 , то и
, то и 
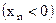 , начиная с некоторого номера.
, начиная с некоторого номера.
Для доказательства следует применить предыдущее утверждение, выбрав  .
.
Теорема 3. Если последовательность  имеет предел, то она ограничена.
имеет предел, то она ограничена.
■ Так как 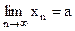 , то по определению предела последовательности
, то по определению предела последовательности 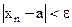 для
для 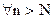 . Но
. Но  , следовательно,
, следовательно,  ; откуда
; откуда  для
для 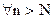 .
.
Обозначим  . Тогда для всех n
. Тогда для всех n  , что и означает ограниченность последовательности
, что и означает ограниченность последовательности  . ■
. ■
Теорема 4. Последовательность  не может стремиться одновременно к двум различным пределам.
не может стремиться одновременно к двум различным пределам.
■ Предположим, что  и
и 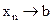 , причем
, причем  . Выберем любое число
. Выберем любое число  ,
, 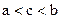 . Так как
. Так как  и
и 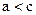 , то существует такой номер
, то существует такой номер  , что для
, что для 
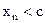 (на основании теоремы 1). С другой стороны, так как
(на основании теоремы 1). С другой стороны, так как 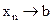 и
и  , то существует такой номер
, то существует такой номер  , что для
, что для 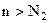
 . Тогда для N, большего
. Тогда для N, большего  и
и  ,
,  одновременно и больше c и меньше c. Полученное противоречие доказывает утверждение. ■
одновременно и больше c и меньше c. Полученное противоречие доказывает утверждение. ■
3. Бесконечно малые и бесконечно большие последовательности
Определение 1.Последовательность  называется бесконечно малой, если
называется бесконечно малой, если  .
.
Если в определении 1 положить 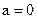 , то неравенство (2.1) примет вид
, то неравенство (2.1) примет вид 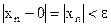 . Следовательно, определение бесконечно малой последовательности может быть сформулировано следующим образом.
. Следовательно, определение бесконечно малой последовательности может быть сформулировано следующим образом.
Определение 2.Последовательность  называется бесконечно малой, если для любого сколь угодно малого
называется бесконечно малой, если для любого сколь угодно малого  существует такой номер N, что для
существует такой номер N, что для 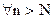
 .
.
(  – бесконечно малая
– бесконечно малая 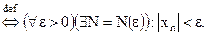 )
)
Пример 1. Последовательность 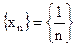 является бесконечно малой.
является бесконечно малой.
В самом деле, 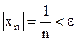 лишь только
лишь только 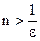 . Следовательно, в качестве
. Следовательно, в качестве  можно взять целую часть числа
можно взять целую часть числа 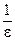 . Заметим, что ни одно отдельно взятое значение бесконечно малой последовательности (если оно не нуль) не может рассматриваться как «малое». Дело в том, что это переменная величина, которая лишь в процессе своего изменения способна сделаться меньшей произвольно выбранного числа
. Заметим, что ни одно отдельно взятое значение бесконечно малой последовательности (если оно не нуль) не может рассматриваться как «малое». Дело в том, что это переменная величина, которая лишь в процессе своего изменения способна сделаться меньшей произвольно выбранного числа  .
.
Вернемся к общему случаю существования предела последовательности.
Если  , то разность
, то разность  будет бесконечно малой, так как в силу (1)
будет бесконечно малой, так как в силу (1)  при
при 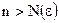 .
.
Обратно, если 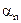 – бесконечно малая, то
– бесконечно малая, то  . Эти рассуждения приводят к следующему утверждению.
. Эти рассуждения приводят к следующему утверждению.
Теорема 1. Для того, чтобы последовательность  имела своим пределом число a, необходимо и достаточно, чтобы последовательность
имела своим пределом число a, необходимо и достаточно, чтобы последовательность 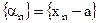 была бесконечно малой.
была бесконечно малой.
Итак, если 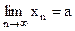 , то
, то 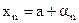 , где
, где  – бесконечно малая, и обратно, если
– бесконечно малая, и обратно, если  , то
, то 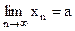 .
.
Бесконечно малым последовательностям противопоставляются в некотором смысле бесконечно большие последовательности.
Определение 3.Последовательность  называется бесконечно большой, если для любого сколь угодно большого числа
называется бесконечно большой, если для любого сколь угодно большого числа 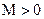 существует такой номер
существует такой номер  , что
, что 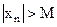 для всех номеров
для всех номеров 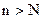 .
.
Как и в случае бесконечно малых, следует заметить, что ни одно отдельно взятое значение бесконечно большой не может рассматриваться как «большое». Это переменная величина, которая лишь в процессе своего изменения способна сделаться большей произвольно взятого числа M.
Пример 2. Последовательность 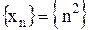 является бесконечно большой, так как
является бесконечно большой, так как  , лишь только
, лишь только 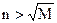 . Следовательно, в качестве
. Следовательно, в качестве  можно взять целую часть числа
можно взять целую часть числа 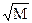 .
.
Если последовательность  бесконечно большая, то говорят также, что она имеет предел
бесконечно большая, то говорят также, что она имеет предел  или стремится к
или стремится к  и записывают
и записывают
 (
(  ).
).
Если при этом бесконечно большая сохраняет определенный знак, то в соответствии со знаком говорят, что 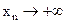 или
или 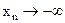 (
( 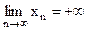 либо
либо 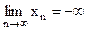 ).
).
( 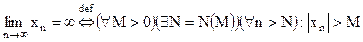 .)
.)
Существует связь между бесконечно большими и бесконечно малыми последовательностями, которая устанавливается теоремой 6.
| <== предыдущая лекция | | | следующая лекция ==> |
| Дубильні речовини | | | Влив технологічних факторів на стан вітамінів |