
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Дубильні речовини
Дата добавления: 2015-10-12; просмотров: 601
|
|
Рассмотрим теоремы, отражающие свойства сходящихся последовательностей и облегчающие нахождение пределов.
Теорема 1. Если последовательности  и
и 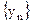 имеют конечные пределы (
имеют конечные пределы (  ,
,  ), то:
), то:
1) их сумма (разность) также имеет конечный предел, причем  ;
;
2) произведение их также имеет конечный предел, причем  ;
;
3) отношение их также имеет конечный предел, причем 

 .
.
■ Так как существуют  и
и  , то
, то 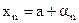 ,
,  , где
, где 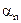 и
и  – бесконечно малые. Тогда
– бесконечно малые. Тогда  . В этом равенстве
. В этом равенстве 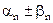 – бесконечно малая по свойству бесконечно малых. Следовательно,
– бесконечно малая по свойству бесконечно малых. Следовательно,  .
.
Рассмотрим  . В силу следствий из теоремы 8 выражение, стоящее в скобках, есть бесконечно малая; следовательно,
. В силу следствий из теоремы 8 выражение, стоящее в скобках, есть бесконечно малая; следовательно,  .
.
Для доказательства 3) рассмотрим разность
 .
.
Выражение в скобках есть бесконечно малая в силу следствий из теоремы 8. Так как  , то, начиная с некоторого номера
, то, начиная с некоторого номера  , где C – некоторое число. Тогда
, где C – некоторое число. Тогда  , начиная с некоторого номера. Следовательно, произведение
, начиная с некоторого номера. Следовательно, произведение 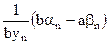 будет бесконечно малым, а оно является разностью между переменной
будет бесконечно малым, а оно является разностью между переменной  и числом
и числом  . Значит,
. Значит,  .■
.■
Теорема 2. Если для последовательностей  и
и 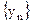
 для всех n и
для всех n и  ,
,  , где a и b конечны, то
, где a и b конечны, то  .
.
■ Предположим, что  . Возьмем число c так, что
. Возьмем число c так, что 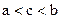 . Тогда существует такой номер
. Тогда существует такой номер  , что
, что 
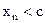 ; с другой стороны, существует такой номер
; с другой стороны, существует такой номер  , что
, что 
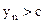 . Выберем
. Выберем 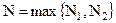 . Тогда для
. Тогда для 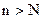 одновременно выполняются оба неравенства
одновременно выполняются оба неравенства 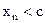 ,
, 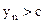 , откуда
, откуда  для
для 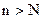 . Полученное противоречие и доказывает теорему. ■
. Полученное противоречие и доказывает теорему. ■
Теорема 3 (предел промежуточной последовательности). Если для последовательностей  ,
, 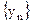 ,
,  при всех n выполнены неравенства
при всех n выполнены неравенства  и
и  , то
, то  .
.
■ Так как  , то для любого произвольного
, то для любого произвольного  существуют такие номера
существуют такие номера  и
и  , что
, что
 для
для  ,
,  для
для 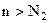 .
.
Тогда для 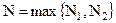 и
и 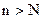
 при
при 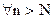 , то есть
, то есть
 при
при 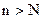 , откуда следует, что
, откуда следует, что  . ■
. ■
| <== предыдущая лекция | | | следующая лекция ==> |
| Влив технологічних факторів на стан вітамінів | | | Що з названого є об’єктом сумісної власності подружжя! |