
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Медичне обслуговування.
Дата добавления: 2015-10-15; просмотров: 719
|
|
Закон сохранения импульса имеет большое значение для исследования реактивного движения.
Под реактивным движением понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно него. (Например, при истечении продуктов сгорания из сопла реактивного летального аппарата). При этом появляется так называемая реактивная сила, толкающая тело.
Наблюдать реактивное движение можно очень просто. Надуйте детский резиновый шарик и отпустите его. Шарик стремительно полетит (рис. 5.4). Движение, правда, будет кратковременным. Реактивная сила действует лишь до тех пор, пока продолжается истечение воздуха. Главная особенность реактивной силы в том, что она возникает в результате взаимодействия частей системы без какого-либо взаимодействия с внешними телами. В нашем примере шарик летит за счет взаимодействия с вытекающей из него струей воздуха. Сила же, сообщающая ускорение пешеходу на земле, пароходу на воде или винтовому самолету в воздухе, возникает только за счет взаимодействия этих тел с землей, водой или воздухом.
Рассмотрим примеры решения задач на применение закона сохраенния импульса и реактивное движение.
1. Вагон массы 10т с автоматической сцепкой, движущийся со скоростью 12м/с, догоняет такой же вагон массы 20т, движущийся со скоростью 6м/с, и сцепляется с ним. Двигаясь дальше вместе, оба вагона сталкиваются со стоящим на рельсах третьим вагоном массы 7,5т. Найти скорости движения вагонов на разных участках пути. Трением пренебречь.
Дано:
m1 = 10  кг
m2 = 20 кг
m2 = 20  кг
m3 = 7,5 кг
m3 = 7,5  кг кг
 1 =12м/с 1 =12м/с
 2 = 6м/с 2 = 6м/с
|  Решение:
На основании закона сохранения импульса имеем Решение:
На основании закона сохранения импульса имеем
 ,
Где ,
Где  - общая скорость движения двух вагонов, - общая скорость движения двух вагонов,  -трех вагонов.
Решая уравнение -трех вагонов.
Решая уравнение 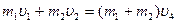 , находим , находим
 Из уравнения
Из уравнения  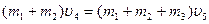 находим находим
 Подставляем числовые значения
Подставляем числовые значения
 = (10·103·12+ 20 = (10·103·12+ 20  ·6) / (10 ·6) / (10  +20 +20  ) = 8 (м/с) ) = 8 (м/с) 
 = 6,4 м/с
Ответ: = 6,4 м/с
Ответ:  = 8 м/с; = 8 м/с;  = 6,4 м/с = 6,4 м/с
|
 -? -?
 -? -?
|
2. Пуля вылетает из винтовки со скоростью  п = 900м/с. Найти скорость винтовки при отдаче, если ее масса mв в 500 раз больше массы пули mп.
п = 900м/с. Найти скорость винтовки при отдаче, если ее масса mв в 500 раз больше массы пули mп.
Дано:
 п = 900м/с
mв = 500 mп п = 900м/с
mв = 500 mп
| Решение:
Импульс винтовки с пулей до выстрела равнялся нулю. Поскольку можно считать, что система винтовки- пуля при выстреле изолирована (действующие на систему внешние силы не равны нулю, но уравнивают друг друга), ее импульс останется неизменным. Спроектировав все импульсы на ось, параллельную скорости пули и совпадающую с ней по направлению, мы можем записать
 ; отсюда ; отсюда  . .
 в = - в = -  Знак « - »указывает, что направление скорости винтовки противоположно направлению скорости пули.
Знак « - »указывает, что направление скорости винтовки противоположно направлению скорости пули.
 Ответ:
Ответ:  в = в = 
|
 в -? в -?

|
3.  Граната, летевшая со скоростью
Граната, летевшая со скоростью  =15м/с, разорвалась на две части с массами m1= 6кг и m2=14кг. Скорость большего осколка
=15м/с, разорвалась на две части с массами m1= 6кг и m2=14кг. Скорость большего осколка  2=24м/с направлена так же, как и скорость гранаты до взрыва. Найти направление и модуль скорости меньшего осколка.
2=24м/с направлена так же, как и скорость гранаты до взрыва. Найти направление и модуль скорости меньшего осколка.
Дано:
 =15м/с
m1= 6кг
m2=14кг =15м/с
m1= 6кг
m2=14кг
 2=24м/с 2=24м/с
| Решение:
За время разрыва гранаты ее импульс изменяется из-за действия силы тяжести незначительно, так как изменение импульса гранаты равно  , а время , а время  разрыва очень мало. Поэтому гранату и ее осколки во время разрыва можно считать изолированной системой. На основании закона сохранения импульса. разрыва очень мало. Поэтому гранату и ее осколки во время разрыва можно считать изолированной системой. На основании закона сохранения импульса.

|
 1 - ? 1 - ?
|
Так как направления скоростей  и
и  2 совпадают, то скорость
2 совпадают, то скорость  1 будет иметь либо то же
1 будет иметь либо то же
направление, либо противоположное ему. Совместим с этим направлением ось координат, при-
нимая направление векторов  и
и  2 за положительное направление оси. Спроектируем урав-
2 за положительное направление оси. Спроектируем урав-
нение на выбранную ось координат. Получим скалярное уравнение
 или
или

Подставим числовые значения и вычислим: 
Знак « - » указывает, что скорость  1направлена в сторону, противоположную направлению полета гранаты.
1направлена в сторону, противоположную направлению полета гранаты.
Ответ: 
4. Два шара массы, которых m1=0,5 кг и m2=0,2 кг, движутся по гладкой горизонтальной поверхности навстречу друг другу со скоростями  и
и  . Определите их скорость
. Определите их скорость  после центрального абсолютно неупругого удара.
после центрального абсолютно неупругого удара.
Дано:
m1=0,5 кг
m2=0,2 кг
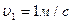

| Решение
Ось ОХ направим вдоль линии, проходящей через центры движущихся шаров по направлению скорости  .
После абсолютно неупругого удара шары движутся с одной и той же скоростью .
После абсолютно неупругого удара шары движутся с одной и той же скоростью  . Так как вдоль оси ОХ внешние силы не действуют (трения нет), то сумма проекции импульсов на эту ось сохраняется ( сумма проекций импульсов обоих шаров до удара равна проекции общего импульса системы после удара). . Так как вдоль оси ОХ внешние силы не действуют (трения нет), то сумма проекции импульсов на эту ось сохраняется ( сумма проекций импульсов обоих шаров до удара равна проекции общего импульса системы после удара).
|
 - ? - ?
|
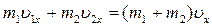 .
.
Так как  , а
, а  , то
, то  .
.
После удара шары будут двигаться в отрицательном направлении оси ОХ со скоростью 0,4 м/с.
Ответ:  = 0,4 м/с
= 0,4 м/с
5. Два пластилиновых шарика, отношение масс которых m2/m1=4, после соударения слиплись и стали двигаться по гладкой горизонтальной поверхности со скоростью  (см.рис.). Определите скорость легкого шарика до соударения, если он двигался в 3 раза быстрее тяжелого (
(см.рис.). Определите скорость легкого шарика до соударения, если он двигался в 3 раза быстрее тяжелого (  ), а направления движения шариков были взаимно перпендикулярны. Трением пренебречь.
), а направления движения шариков были взаимно перпендикулярны. Трением пренебречь.
Дано:
m2/m1 = 4

| Решение
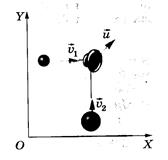 Так как скорости Так как скорости  и и  шариков взаимно перпендикулярны, то оси прямоугольной системы координат удобно направить параллельно этим скоростям.
Согласно закону сохранения импульса имеем шариков взаимно перпендикулярны, то оси прямоугольной системы координат удобно направить параллельно этим скоростям.
Согласно закону сохранения импульса имеем
 . .
|
| m1 - ? |
Запишем это уравнение в проекциях на оси ОХ и ОY, проведенные так, как пока
зано на рисунке : 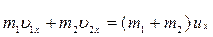 ,
,
 .
.
Так как  , то
, то  .
.
Модуль скорости  равен:
равен:  .
.
Итак,  ,следовательно,
,следовательно, 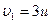 .
.
Задания для самостоятельного решения
1. Два шара массы, которых m1 и m2, движутся по гладкой горизонтальной поверхности навстречу друг другу со скоростями  и
и  . Определите их скорость
. Определите их скорость  после центрального абсолютно неупругого удара.
после центрального абсолютно неупругого удара.
| № вар | |||||||||||||
| m1 | |||||||||||||
| m2 | |||||||||||||

| |||||||||||||

|
2. Вагон массы m1 с автоматической сцепкой, движущийся со скоростью  , догоняет такой же вагон массы m2, движущийся со скоростью
, догоняет такой же вагон массы m2, движущийся со скоростью  , и сцепляется с ним. Двигаясь дальше вместе, оба вагона сталкиваются со стоящим на рельсах третьим вагоном массы m3. Найти скорости движения вагонов на разных участках пути. Трением пренебречь.
, и сцепляется с ним. Двигаясь дальше вместе, оба вагона сталкиваются со стоящим на рельсах третьим вагоном массы m3. Найти скорости движения вагонов на разных участках пути. Трением пренебречь.
| № вар | |||||||||||||
| m1 | |||||||||||||
| m2 | |||||||||||||

| |||||||||||||
| m3 |
3. решить задачи
Варианты 1,6,11,16,21,26 задачу № 4
Варианты 2,7,12,17,22,27 задачу № 5
Варианты 3,8,13,18,23,28 задачу № 6
Варианты 4,9,14,19,24,29 задачу № 7
Варианты 5,10,15,20,25,30 задачу № 8
4. Стоящий на льду человек массой m1 =60 кг ловит мяч массой m2 =0,50 кг, который летит горизонтально со скоростью  =20м/с. На какое расстояние откатится человек с мячом по горизонтальной поверхности льда, если коэффициент трения k=0,050?
=20м/с. На какое расстояние откатится человек с мячом по горизонтальной поверхности льда, если коэффициент трения k=0,050?
5. Из винтовки массой 4,0 кг вылетает пуля массой 10 г со скоростью 700 м/с. Какова скорость отдачи винтовки при выстреле, если она подвешена горизонтально на нитях? На какую высоту поднимается винтовка после выстрела?
6. Снаряд массой 4,0 кг вылетает из ствола орудия в горизонтальном направлении со скоростью 1000 м/с. Определить среднюю силу сопротивления противооткатных устройств, если длина отката ствола по направляющим неподвижного орудия 1,0 м, а масса ствола 320кг.
7. Ракета, масса которой без топлива m1 =400 г, при сгорании топлива поднимается на высоту h=125м. Масса топлива m2 =50г. определить скорость выхода газов из ракеты  , считая, что сгорание топлива происходит мгновенно.
, считая, что сгорание топлива происходит мгновенно.
8. Плот массой m1=400кг и длиной l =10м покоится в неподвижной воде. Два мальчика с массами m2 =60 кг и m3 =40кг, стоящие на противоположных концах плота, одновременно начинают двигаться навстречу друг другу с одинаковой скоростью и останавливаются при встрече. На какое расстояние при этом сместится плот?
Реактивное движение. Формула Циолковского.
На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью U относительно ракеты. Обозначим массу выброшенных газов через m, а массу ракеты после истечения газов через M. Тогда для замкнутой системы «ракета + газы» можно записать на основании закона сохранения импульса (по аналогии с задачей о выстреле из орудия): , V= - 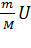 где V – скорость ракеты после истечения газов.
где V – скорость ракеты после истечения газов.
Здесь предполагалось, что начальная скорость ракеты равнялась нулю.
Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.
Для получения точной формулы процесс истечения газа из сопла ракеты нужно рассмотреть более детально. Пусть ракета в момент времени t имеет массу M и движется со скоростью V. В течение малого промежутка времени Δt из ракеты будет выброшена некоторая порция газа с относительной скоростью U. Ракета в момент t + Δt будет иметь скорость  а ее масса станет равной M + ΔM, где ΔM < 0 (рис. 1.17.3 (2)). Масса выброшенных газов будет, очевидно, равна –ΔM > 0. Скорость газов в инерциальной системе OX будет равна V+U. Применим закон сохранения импульса. В момент времени t + Δt импульс ракеты равен (
а ее масса станет равной M + ΔM, где ΔM < 0 (рис. 1.17.3 (2)). Масса выброшенных газов будет, очевидно, равна –ΔM > 0. Скорость газов в инерциальной системе OX будет равна V+U. Применим закон сохранения импульса. В момент времени t + Δt импульс ракеты равен (  )( M + ΔM)а импульс испущенных газов равен
)( M + ΔM)а импульс испущенных газов равен  В момент времени t импульс всей системы был равен MV. Предполагая систему «ракета + газы» замкнутой, можно записать:
В момент времени t импульс всей системы был равен MV. Предполагая систему «ракета + газы» замкнутой, можно записать: 
Величиной  можно пренебречь, так как |ΔM| << M. Разделив обе части последнего соотношения на Δt и перейдя к пределу при Δt → 0, получим
можно пренебречь, так как |ΔM| << M. Разделив обе части последнего соотношения на Δt и перейдя к пределу при Δt → 0, получим 
Величина  есть расход топлива в единицу времени. Величина
есть расход топлива в единицу времени. Величина  называется реактивной силой тяги Fp Реактивная сила тяги действует на ракету со стороны истекающих газов, она направлена в сторону, противоположную относительной скорости. Соотношение Ma=Fp=-
называется реактивной силой тяги Fp Реактивная сила тяги действует на ракету со стороны истекающих газов, она направлена в сторону, противоположную относительной скорости. Соотношение Ma=Fp=-  U
U
выражает второй закон Ньютона для тела переменной массы. Если газы выбрасываются из сопла ракеты строго назад (рис. 1.17.3), то в скалярной форме это соотношение принимает вид:
| Ma = μu, |
где u – модуль относительной скорости. С помощью математической операции интегрирования из этого соотношения можно получить формулу для конечной скорости υ ракеты:
где  – отношение началь
– отношение началь  ной и конечной масс ракеты. Эта формула называется формулой Циолковского. Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости υ = υ1 = 7,9·103 м/с при u = 3·103 м/с (скорости истечения газов при сгорании топлива бывают порядка 2–4 км/с) стартовая масса одноступенчатой ракеты должна примерно в 14 раз превышать конечную массу. Для достижения конечной скорости υ = 4u отношение
ной и конечной масс ракеты. Эта формула называется формулой Циолковского. Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости υ = υ1 = 7,9·103 м/с при u = 3·103 м/с (скорости истечения газов при сгорании топлива бывают порядка 2–4 км/с) стартовая масса одноступенчатой ракеты должна примерно в 14 раз превышать конечную массу. Для достижения конечной скорости υ = 4u отношение  должно быть = 50.
должно быть = 50.
Значительное снижение стартовой массы ракеты может быть достигнуто при использовании многоступенчатых ракет, когда ступени ракеты отделяются по мере выгорания топлива. Из процесса последующего разгона ракеты исключаются массы контейнеров, в которых находилось топливо, отработавшие двигатели, системы управления и т. д. Именно по пути создания экономичных многоступенчатых ракет развивается современное ракетостроение.
| <== предыдущая лекция | | | следующая лекция ==> |
| ДЛЯ КОЖНОГО ГРОМАДЯНИНА | | | Зрошування та МТЗ для тепличного господарства. |