CONTENTS

Дата добавления: 2015-10-18; просмотров: 522

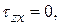
В случае плоского напряженного состояния равными нулю будут также коэффициент и один из корней характеристического уравнения (4.17), то есть одно из главных напряжений обращается в нуль. При этом уравнение (4.17) перейдет в следующее

, (4.19)

корни которого определяются равенствами

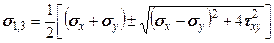. (4.20)

В случае линейного напряженного состояния два главных напряжения будут равны нулю, т. е. в уравнении (4.14) коэффициенты .

Главные напряжения обладают важным свойством: нормальные напряжения на главных площадках принимают экстремальные значения.

Теперь докажем ортогональность главных площадок. Сначала это сделаем для первой и второй главных площадок. Пусть направляющие косинусы первой главной площадки будут 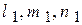, а второй - . Выпишем уравнения (4.15) для первой и второй главных площадок в виде

(4.21)

, .

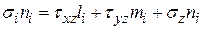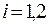Далее поступим следующим образом. Умножим уравнения (4.21) первой группы 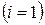соответственно на , а уравнения второй группы 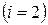- на , а затем сложим все уравнения первой группы и отдельно второй. Вычитая из первой суммы вторую, получаем

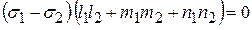. (4.22)

Из анализа уравнения (4.22) видно, что при

.

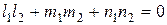Последнее равенство и есть условие ортогональности первой и второй главных площадок. Аналогично доказывается ортогональность других главных площадок.

Напряжения на косых площадках при плоском напряженном состоянии

Рассмотрим напряженное состояние пластинки толщиной , находящейся под действием сил Р, лежащих в плоскости пластинки (рис. 4.6). Будем считать, что под действием внешних сил пластинка находится в плоском напряженном состоянии, значит . В выделенном элементе пластинки напряжения , и 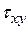лежат в одной плоскости, поэтому напряженное состояние и называется плоским.

Пусть заданы напряжения на площадках и элемента ABC. Надо определить нормальные напряжения и касательные на площадке BC, нормаль к которой составляет угол с осью x. Массовыми силами, действующими на элемент ABC, пренебрегаем.

В случае плоского напряженного состояния тензор напряжений примет вид

.

Рис. 4.6. К определению напряжений на косых площадках

Величины и определим из условия равновесия элемента ABC, составив соответствующие уравнения в проекциях на оси и . Опуская промежуточные математические выкладки, окончательно получим

, (4.23)

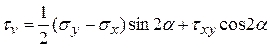. (4.24)

Если аналогично вычислить напряжения на площадке, нормаль к которой r перпендикулярна вектору нормали , то получим

, (4.25)

. (4.26)

Полученные формулы позволяют выявить важные закономерности. Так, складывая (4.23) и (4.25), имеем

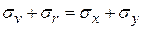. (4.27)

Видно, что сумма нормальных напряжений на произвольных взаимно перпендикулярных площадках при их повороте не меняется.

Сопоставляя (4.24) и (4.26), видим

, (4.28)

т. е. касательные напряжения, действующие на произвольных взаимно перпендикулярных площадках, подчиняются закону парности.

Положение главных площадок (касательные напряжения равны нулю) можно найти из (4.24) или (4.26), полагая 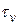или , следовательно

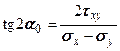, (4.29)

где — угол, который составляет нормаль или главной площадки с осью .

Можно показать, что при заданных значениях , и 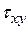на некоторых известных взаимно перпендикулярных площадках, нормальные напряжения на главных площадках определяются соотношением (см. формулу (4.20))

. (4.30)

Обратная задача - если известны главные напряжения 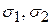, то формулы для определения напряжений на наклонных площадках примут вид

,

, (4.31)

.

Тема 5. Основы теории деформированного состояния. Объемная деформация. Обобщенный закон Гука