ТЕМА 10.

Дата добавления: 2015-10-19; просмотров: 471

Одно из главных изобретений 19 века – механизм вентилей для духовых инструментов, с помощью которого возможности духовых музыкальных инструментов стали гораздо шире; появились новые инструменты – например туба и флейта-пикколо. Кроме того, то пианино, на котором мы играем сегодня, было изобретено в то же время в Америке и сразу же приобрело небывалую популярность и в России.

ЛАБОРАТОРНАЯ РАБОТА №5 ИССЛЕДОВАНИЕ ЧАСТОТНЫХ XАРАКТЕРИСТИК ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ И СОЕДИНЕНИЙ ЗВЕНЬЕВ

Цель работы:получение навыков по построению частотных характеристик и исследованию влияния параметров звеньев на характер и показатели частотных характеристик.

Порядок выполнения работы

1. Для звеньев или соединений звеньев, заданных передаточными функциями:

, (5.1)

, (5.2)

, (5.3)

, (5.4)

, (5.5)

, (5.6)

, (5.7)

, (5.8)

построить АФЧХ, АЧХ, ФЧХ, ЛАХ при различных значениях параметров.

2. Для заданной преподавателем передаточной функции промоделировать прохождение через исследуемый объект гармонического сигнала с различной частотой

Теоретические сведения

Амплитудно-фазовой (частотной) характеристикой (АФЧХ) называется функция W(jw), определяющая изменение амплитуды и фазы выходной величины системы или ее отдельного элемента в установившемся режиме при приложении на входе гармонического воздействия. АФЧХ можно определить как преобразование Фурье весовой функции объекта или системы:

, (5.9)

либо формальным переходом от передаточной функции W(s) при замене s на jw. Для 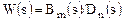, где и - многочлены m-й и n-й степеней от s, частотная характеристика будет равна

. (5.10)

Освобождаясь от мнимого числа в знаменателе, путем домножения на комплексно сопряженную знаменателю функцию получаем

,

где R(w), I(w) – вещественная и мнимая части частотной функции системы.

(5.11)

. (5.12)

Представляя комплексные функции числителя и знаменателя (5.10) в показательной форме, можно записать:

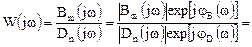
(5.13)

,

или

(5.14)

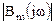где и 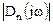– модули комплексных функций числителя и знаменателя частотной характеристики,

j_B(w),j_D(w) – соответственно фазы комплексных функций числителя и знаменателя,

А(w) – амплитудно-частотная характеристика (АЧХ), равная

, (5.15)

j(w) – фазовая частотная характеристика (ФЧХ),

. (5.16)

Если рассматривать прохождение гармонического сигнала через линейный объект, то при сохраняющейся частоте сигнала амплитудно-частотная характеристика также определяется как зависимость отношения амплитуды выходного гармонического сигнала в установившемся режиме к амплитуде входного сигнала от частоты сигнала. Соответственно, фазовая частотная характеристика есть зависимость смещения по фазе выходного гармонического сигнала относительно входного от частоты сигнала.

В MathCad для выделения значения фазы предусмотрена функция arg():

, (5.17)

либо функция atan, определяющие значения фазы только в пределах от -p до +p. Если фаза выходит за пределы (-p,+p), ее необходимо скорректировать с учетом знаков действительной и мнимой частей АФЧХ.

Графически амплитудно-фазовая частотная характеристика изображается на комплексной плоскости в полярных координатах (А, j) как годограф функции W(jw). Можно построить амплитудно-частотную характеристику и в прямоугольных координатах (Im[W(jw)], Re[W(jw)]). При этом частоту w изменяют от 0 до ¥.

Логарифмические частотные характеристикииспользуются при исследовании систем автоматического управления с помощью частотных методов и представляют собой логарифмическую амплитудную и логарифмическую фазовую характеристики.

Логарифмической амплитудной частотной характеристикой (ЛАХ) называется кривая, соответствующая 20 десятичным логарифмам модуля частотной характеристики системы, построенная в логарифмической координатной сетке: логарифм амплитуды – логарифм частоты (или частота, отложенная в декадах):

, (5.18)

где – логарифм частоты.

При построении логарифмической амплитудной характеристики по оси ординат откладывают величину , единицей измерения для которой является децибел. По оси абсцисс – логарифм частоты q. Равномерной единицей на оси абсцисс является декада – отрезок, на котором значение частоты увеличивается в 10 раз. Точка пересечения ЛАХ с осью абсцисс называется частотой среза w_с.

Значению А(w)= 1 исходя из (5.18) соответствует , в этом случае ЛАХ проходит по оси абсцисс. Верхняя полуплоскость ЛАХ соответствует значениям А(w) > 1 (усиление амплитуды), а нижняя полуплоскость – значениям А(w) < 1 (ослабление амплитуды).

При построении логарифмической фазовой характеристики (ЛФХ) отсчет углов j(w) идет по оси ординат в обычном масштабе в радианах либо градусах, а по оси абсцисс откладывается логарифм частоты q или частота в декадах.

Логарифмические частотные характеристики удобны для анализа систем, образованных последовательным соединением элементарных звеньев (рис. 5.1), поскольку позволяют перейти от операции умножения модулей частотных характеристик элементарных звеньев к операции сложения их логарифмических амплитудных характеристик, что иллюстрируется следующими зависимостями:

, (5.20)

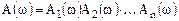, (5.21)

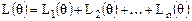. (5.22)