ТЕМА 11.

Дата добавления: 2015-10-19; просмотров: 569

В MathCad комплексные вычисления производятся с помощью символьного процессора. Для выполнения операций над комплексными числами мнимую единицу j необходимо заранее задать как 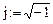, либо использовать стандартную мнимую переменную i коэффициентом 1 - . По окончании редактирования формулы запись приобретает вид: i.

Запишем частотную передаточную функцию апериодического звена первого порядка:

.

При выходе из редактирования (щелчок мыши в свободном поле документа) формула приобретет вид:

.

Выделим действительную и мнимую части амплитудно-фазовой частотной характеристики, используя функцию complex, которую можно выбрать в панели инструментов «Математика» в меню «Символы»:

,

.

Для построения графиков частотных характеристик необходимо задать диапазон изменения частоты, например, , коэффициент усиления и постоянную времени .

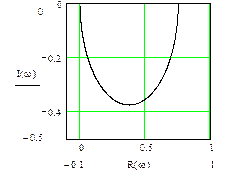
Рис.5.2. Комплексная частотная характеристика

Амплитудная частотная характеристика рассчитывается следующим образом:

.

Использование функции simplify позволяет упростить результат вычислений. Однако последняя запись, полученная с помощью MathCad, может быть представлена в более удобном виде: .

Рис.5.3. Амплитудная частотная характеристика

Фазовую частотную характеристику определим с помощью функции atan

.

Рис.5.4. Фазовая частотная характеристика

Логарифмическая амплитудная характеристика рассчитывается как

Рис.5.5. Логарифмическая амплитудная частотная характеристика

При построении асимптотической ЛАХ, представляющей собой кусочно-линейную функцию, можно воспользоваться программным модулем (панель "Инструменты программирования"). Для передаточной функции апериодического звена первого порядка асимптотическая ЛАХ может быть построена по программе:

Рис.5.6. Асимптотическая ЛАХ

Моделирование прохождения гармонического сигнала через линейную систему осуществляется путем решения дифференциального уравнения с гармонической правой частью

.

Преобразование Лапласа от входного гармонического сигнала :

.

Выходной сигнал y(s) в преобразованиях Лапласа имеет вид:

.

Выполняем обратные преобразования Лапласа и записываем выходной сигнал:

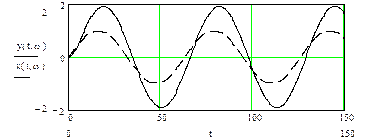
Рис.5.7. Сигналы на входе и выходе звена для w=0.1

Рис.5.8. Сигналы на входе и выходе звена для w=0.5

Рис.5.9. Сигналы на входе и выходе звена для w=5

Как видно из рисунков, при постоянной амплитуде входного гармонического сигнала, амплитуда сигнала на выходе апериодического звена с возрастанием частоты существенно уменьшилась, а смещение сигналов по фазе приблизилось к p/2. Апериодическое звено работает как фильтр высоких частот.

Контрольные вопросы

1. Дать определение амплитудной и фазовой частотных характеристик, ЛАХ, АФЧХ?

2. Что такое частота среза и полоса пропускания ЛАХ?

3. Построить частотные характеристики для апериодического звена первого порядка, звеньев второго порядка, интегрирующего и дифференцирующего звеньев?

4. Как получить амплитудную и фазовую частотные характеристики при последовательном и параллельном соединении звеньев?

5. Как влияют значения постоянных времени звена на полосу пропускания ЛАХ?

6. Как построить асимптотическую ЛАХ по передаточной функции?

Содержание отчета

Отчет должен содержать: