Тема № 5. Українська культура козацько-гетьманської доби

Дата добавления: 2015-10-19; просмотров: 418

Значение теоретической НКФ в любой точке равно нулю, т.к не имеются коэффициентов . Погрешность модели MA(0) = 1.6354.

Модели ARMA(M,N)

Построим модели авторегрессии-скользящего среднего ARMA(M,N) порядков M,N = 1, 2, 3.

Для этого воспользуемся уравнениями связей параметров ARMA(M,N) с корреляционной функцией

Таблица 5 - уравнения связей параметров ARMA(M,N) с корреляционной функцией

Для модели ARMA(2,3) получим следующую систему:

Решив все полученные системы уравнений, а также подсчитав теоретические НКФ для каждой смешанной модели ARMA(M,N) по формуле:

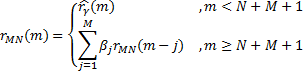
получим следующую таблицу параметров моделей ARMA(M,N):

Таблица 6 – коэффициенты моделей ARMA(M,N)

Модель ARMA(M,N)								Погрешность
ARMA(1,1)	Модель не существует!
ARMA(1,2)	Модель не существует!
ARMA(1,3)	Модель не существует!
ARMA(2,1)	1.0764	-0.7926		10.5102	-0.8868			0.2662
ARMA(2,2)	0.9316	-0.8318		9.4618	0.8366	5.5323		0.0051
ARMA(2,3)	0.9444	-0.8830		-4.8714	1.2166	-12.5896	-2.7796	0.0050
ARMA(3,1)	Модель не устойчива!
ARMA(3,2)	Модель не устойчива!
ARMA(3,3)	Модель не существует!

Проверяя устойчивость полученных моделей с помощью следующих условий:

· модель ARMA (0,N) = MA (N) устойчива всегда,

· модель ARMA (1,N) устойчива только, если

· модель ARMA (2,N) устойчива только, если

· модель ARMA (3,N) устойчива только, если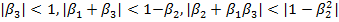

видно, что ARMA(3,1) и ARMA(3,2) не устойчивы, т.к имеет следующие параметры:

Модель ARMA(M,N)
ARMA(3,2)	1.2031	-1.1240	0.2152	5.8695	-2.1152	9.3494
ARMA(3,1)	-4.6848	5.2136	-4.4513	59.7911	10.5333

которые не удовлетворяют условиям устойчивости.