
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Форма трудового договору
Дата добавления: 2015-10-19; просмотров: 923
|
|
16) По цели производится 4 выстрела. Вероятность попадания при каждом выстреле равна 0,4. Построить ряд и многоугольник распределения случайного числа попаданий. Найти F(x), M(x), D(x),  .
.
17) Вероятность выигрыша по лотерейному билету равна 0,2. Куплено 3 билета.
Найти закон распределения и математическое ожидание случайной величины X – числа
выигрышных билетов.
18) Случайная величина X принимает следующие значения с соответствующими вероятностями:

| ||||

| 0,2 | 0,3 | ? | 0,1 |
Найти неизвестную вероятность 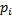 . Найти дисперсию случайной величины. Построить график функции распределения F(x). Построить многоугольник распределения вероятностей.
. Найти дисперсию случайной величины. Построить график функции распределения F(x). Построить многоугольник распределения вероятностей.
19) Дано распределение дискретной случайной величины X. Построить функцию распределения F(x). Найти математическое ожидание и среднее квадратическое отклонение, построить многоугольник распределения вероятностей.

| ||||

| 0,3 | 0,1 | 0,1 | 0,5 |
20) Случайная величина Х задана функцией распределения
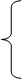
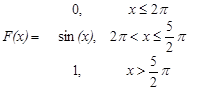
Найти 1) плотность распределения f(х),
2) P 
3) М(х), D(х).
21) Построить график функции распределения F(х).

Найти постоянную c, и дисперсию случайной величины X.
22) Случайная величина Х задана функцией распределения:

Построить график функции распределения F(х).
Найти: 1) плотность распределения вероятности f(х),
2) P (-2<x<4) .
3) М(х), D(х).
23) Случайная величина X задана функцией плотности вероятности

Найти F(x), М(х), D(х), моду, медиану
24) Случайная величина X задана функцией плотности вероятности
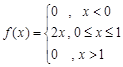
Найти F(x), М(х), D(х), моду, медиану
25) Случайная величина X задана функцией плотности вероятности
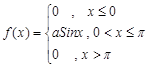
Найти:
1) значение параметра a;
2) функцию распределения F(x);
3) вероятность попадания случайной величины X в интервал (-  ,
, 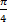 )
)
4) построить графики f(x), F(x).
26) Cлучайная величина Х распределена по нормальному закону с математическим ожиданием а и средним квадратическим отклонением s. Найти: а) вероятность  попадания случайной величины в интервал (х1; х2);
попадания случайной величины в интервал (х1; х2);
б) величину интервала d, в который с заданной вероятностью Р попадает значение случайной величины Х: 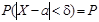 .
.
27) Случайная величина  (нормально распределена, M(X)=2,
(нормально распределена, M(X)=2,  ).
).
Найти вероятность того, что эта случайная величина принимает значение:
а) в интервале (-1, 2);
б) меньшее -1;
в) большее 2;
г) отличающееся от своего среднего значения по абсолютной величине не больше чем на 1.
28) Время обнаружения цели радиолокатором распределено по показательному закону.
10 секунд – среднее время обнаружения цели. Найти вероятность того, что цель будет обнаружена за время от 6 до 12 секунд.
29) Случайная величина X равномерно распределена от 0 до 1. Определить
математическое ожидание и дисперсию случайной величины X
30) Измеряемая случайная величина X подчиняется нормальному закону распределения с параметрами M(X) = 10, σ(X) = 5. Записать выражение плотности распределения X. Найти симметричный относительно M(X) интервал, в который с вероятностью P = 0,99739 попадает измеренное значение.
31) Качество продукции характеризуется двумя случайными параметрами X и Y.
Закон распределения случайной величины Z = (X;Y) представлен в таблице. Найти законы распределения одномерных случайных величин X и Y. Найти условное распределение случайной величины X при условии, что случайная величина Y приняла значение 0,2. Найти условное математическое ожидание с.в. X, при условии, что Y приняла значение 0,2. (в Mathematica можно найти все условные ряды и все условные математические ожидания)
| Y X | 0 | 0,1 | 0,2 | 0,3 |
| 5 | 0,2 | 0,1 | O,05 | 0,05 |
| 6 | 0 | 0,15 | 0,15 | 0,1 |
| 7 | 0 | 0 | 0,1 | 0,1 |
32) Плотность вероятности двумерной случайной величины (X; Y) равна

Найти коэффициент корреляции  .
.
33) Распределение вероятностей двумерной случайной величины (Х,У) задано таблицей. Найти законы распределения составляющих величин X, Y и коэффициент корреляции  .
.
Записать уравнения прямых регрессии.
34) Из большой партии деталей было отобрано 100 деталей. Определить вероятность того, что отклонение средней прочности отобранных деталей от средней прочности партии не превышает 0,3, если дисперсия прочности наугад взятой детали равна 2,25. (использовать теорему Чебышева)
35) Случайная величина ξ имеет дисперсию 0,004. Найти вероятность того, что случайная величина ξ отличается от М[ξ] более чем на 0,2. (использовать неравенство Чебышева)
| <== предыдущая лекция | | | следующая лекция ==> |
| Сфера та порядок укладення колективного договору | | | Фактичний допуск до роботи |