Поняття та історія формування. Ідейно-теоретичні засади

Дата добавления: 2015-03-11; просмотров: 553

Сообщения с дискретным распределением состояний элементов характеризуются множеством возможных сообщений X = (x₁, x₂, … x_i,… x_n) и вероятностями появления этих сообщений p(x₁), p(x₂),…p(x_i),… p(x_n), при этом 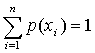. Неопределенность дискретных систем описывается выражением

, (2.1)

Это выражение можно обобщить и на случай непрерывных сообщений. При этом роль распределения вероятности по состояниям в непрерывном случае играет плотность вероятности w(x) (рис.2.1).

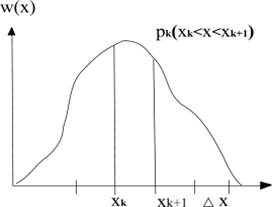
Рис.2.1. Плотность вероятности случайной величины x

Для перехода от дискретных сообщений к непрерывным сообщениям произведем квантование значений случайной непрерывной величины x на счетное число уровней с интервалом Δx. Полученная, таким образом, дискретная случайная величина x характеризуется распределением, в котором вероятность k-го состояния равна , где w(x) - плотность вероятности квантуемой непрерывной величины. Для дискретного случая p_k=w(x)· Δx. Чем меньше Δx тем более точной будет замена. Энтропия эквивалентного сообщения равна

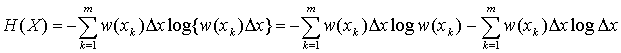
При уменьшении Δx (увеличении m) первая сумма в пределе стремится к интегралу , а вторая сумма при достаточно малом Δx с высокой точностью равна , так как 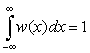и тогда

(2.2)

Обозначим , тогда (2.3)

Величину 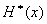называют приведенной или дифференциальной энтропией.

Непрерывные случайные системы сохраняют свои свойства подобно свойствам дискретных систем. Рассмотрим эти свойства:

1. Энтропия объединения равна

,

где ,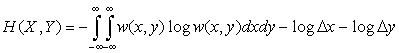

,

2. При любых двух случайных переменных x и y

причем знак равенства будет тогда, когда x и y независимы.

3. Всякое сглаживание огибающей плотности вероятности w(x) приводит только к увеличению энтропии.