Тілесна психотерапія В.Райха

Дата добавления: 2015-03-11; просмотров: 617

Для сравнения сообщений необходимо предварительно вычислить энтропию этих сообщений. Вычислим энтропию сообщений, состояния элементов которых распределены по нормальному закону

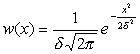
Энтропия равна . Удобнее всего найти энтропию через математическое ожидание

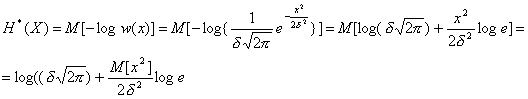
Но так как 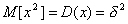, то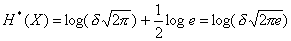

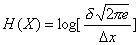(2.14)

Таким образом, получили значение энтропии для нормального закона распределения.

Теперь найдем значение энтропии непрерывных сообщений для равновероятного закона распределения.

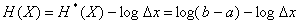
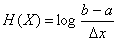(2.15)

Выражение (2.15) представляет энтропию для непрерывных сообщений с равновероятным распределением состояний элементов.

Рассмотрим два вида сообщений, обладающих одинаковой энтропией, но характеризуемых различными законами распределения состояний элементов.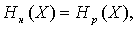

где - энтропия сообщений с нормальным распределением,

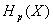- энтропия сообщений с равновероятным распределением.

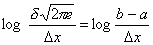далее потенцируя, получим

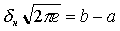(2.16)

Дисперсия для равновероятного закона распределения определяется интегралом

Обозначим 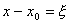, тогда , - представляет среднее значение

,

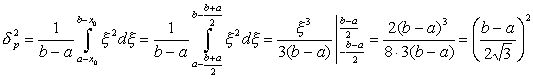откуда , полученное выражение подставим в (2.16).

или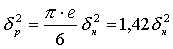

Таким образом, если имеются две системы с одинаковыми значениями энтропии по величине, то дисперсия системы при равновероятном распределении на 42% больше дисперсии системы, имеющей нормальное распределение состояния элементов.

А, как известно, дисперсия характеризует среднюю мощность сигналов. То есть, выгоднее всего передавать сообщения по нормальному закону распределения элементов. Затраты на мощность при нормальном законе будут составлять 0,7 по сравнению с затратами мощности при равновероятном законе распределения элементов.

Епсилон -энтропия (ε-энтропия )

Непрерывные сигналы воспринимаются с ограниченной точностью. Пусть Х - точный сигнал, его плотность вероятности w(x). Сигнал, воспроизводимый любой аппаратурой, отличается от исходного сигнала. То есть, на выходе аппаратуры имеем другой сигнал Y, отличный от X. Критерием близости двух сигналов X и Y является функционал

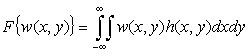, (2.17)

где h(x,y) - некоторая весовая функция, имеющая природу расстояния.

Функционал F по своему виду представляет собой математическое ожидание функции h(x,y) случайных аргументов x и y. Если подобрать подходящим образом эту функцию, то в качестве критерия близости двух сигналов можно использовать условие , где 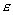– некоторая наперед заданная величина. Обычно используют среднеквадратический критерий

Сигнал Y содержит информацию относительно X в соответствии с выражением

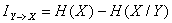
Энтропия H(X) определяется функцией w(x), которая является заданной. Варьируя функцию w(x/y) можно в принципе добиться минимального значения величины 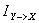при заданных требованиях к точности .

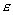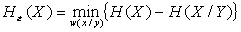_, при ограничении

Таким образом, ε-энтропия величины X называется минимальное количество информации в одной случайной величине Y относительно другой X, при котором удовлетворяется заданное требование к верности воспроизведения величины X.

Пример. Найти ε-энтропию источника информации, ансамбль состояний которого описывается нормальным распределением.

Решение. ε-энтропия определяется по формуле

_,

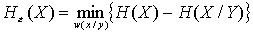но условная энтропия H(X/Y) полностью определяется помехой, поэтому

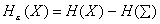
Энтропия сигнала равна 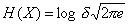, так как сигнал передается по нормальному закону. Помеху определим из наихудших условий, когда она имеет максимальное воздействие. Помеха максимальна, если распределена по нормальному закону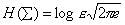

,

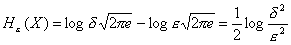где 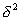- мощность сигнала, - мощность помехи