Windows 7

Дата добавления: 2015-03-11; просмотров: 627

6.1. Волновая функция, описывающая некоторую частицу, может быть представлена в виде Ψ(x,t)=ψ(x,t) . Показать, что плотность вероятности нахождения частицы определяется только координатой ψ-функции

6.2. Электрон находится в потенциальной яме шириной L. В каких точках интервала (0<x<L) плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить значение плотности вероятности для этих точек. Решения пояснить графиком.

6.3. Ψ – функция некоторой частицы имеет вид Ψ = , где r – расстояние этой частицы до силового центра; – некоторая постоянная. Используя условия нормировки вероятностей, определить нормировочный коэффициент A.

6.4. Электрон находится в бесконечно глубокой одномерной потенциальной яме шириной L. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n=2), будет обнаружен в средней трети ящика. Решение пояснить графиком.

6.5.Получить выражение для собственных значений энергии E_n частицы, находящейся в бесконечно глубокой одномерной потенциальной яме шириной L (решить уравнение Шредингера).

6.6. Получить выражение для собственных значений волновой функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме шириной L (решить уравнение Шредингера).

6.7. Частица в потенциальной яме шириной L находится в возбужденном состоянии с n=2. Определить, в каких точках интервала (0<x<L) плотность вероятности нахождения частицы имеет максимальное и минимальное значения.

6.8. Используя условия нормировки вероятностей определить нормировочный коэффициент A волновой функции Ψ = A 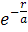, описывающей основное состояние электрона в атоме водорода, где r – расстояние электрона от ядра, a – первый боровский радиус.

6.9. Известно, что собственная волновая функция, описывающая состояние электрона в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками и шириной L, имеет вид Ψ_n(x)= . Определить среднее значение координаты <x> электрона.

6.10.Электрон находится в одномерной прямоугольной потенциальной яме шириной L с бесконечно высокими стенками. Определить вероятность P обнаружения электрона в средней трети ямы, если электрон находится в возбужденном состоянии (n=3). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.