Классическая нормальная линейная регрессионная модельРассмотрим вопрос о качестве МНК-оценок (4) и (5). Эти оценки обладают многими хорошими свойствами, если величины в уравнении (1) удовлетворяют следующим условиям.
При выполнении этих условий соотношение (1) называется классической нормальной линейной регрессионной моделью. Справедлива теорема Гаусса-Маркова: В условиях классической нормальной линейной регрессионной модели* оценки (4) и (5) имеют наименьшую дисперсию в классе всех линейных несмещенных оценок. Оценки, имеющие наименьшую дисперсию, называются эффективными. Таким образом, по теореме Гаусса-Маркова в условиях классической нормальной регрессионной модели МНК-оценки параметров парной линейной регрессии являются эффективными в классе всех линейных несмещенных оценок. Упрощенная интерпретация теоремы Гаусса-Маркова: в среднем оценки (4) и (5) меньше, чем любые другие линейные несмещенные оценки, полученные по данным наблюдениям, отклоняются от истинных (но неизвестных) значений параметров m и b. Кроме того, можно доказать (см., например, [5]), что в условиях классической нормальной регрессионной модели оценки (4) и (5) обладают следующими свойствами#: 1. 2. 3. Для дисперсии оценки
4. 5. Остаточная сумма квадратов Qe независима от
имеет распределение хи-квадрат с числом степеней свободы n -2 (c2 n -2). 6. Cтатистика s 2:
является несмещенной оценкой дисперсии возмущений (Ms 2=s2).
|

 – состоятельные оценки параметров m и b.
– состоятельные оценки параметров m и b. ).
).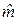 справедлива формула:
справедлива формула: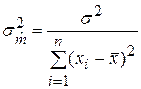 (8)
(8) (8а)
(8а) (8б)
(8б)


