Оперативное слежение за заболеваемостью с помощью метода ВальдаВ основе метода Вальда (1940) лежит сравнение числа ежедневно нарастающей заболеваемости в течение месяца со среднедневным нарастающим числом заболеваний, определенным для каждого календарного месяца на основе многолетних наблюдений. При этом исходным материалом служат абсолютные показатели заболеваемости, рассчитанные по диагнозам экстренных извещений за 5-6 лет и более, предшествовавших периоду оперативного слежения и адекватных по уровню заболеваемости анализируемому периоду. Наиболее эффективно и сравнительно проще по выполнению оперативное слежение за заболеваемостью по дням или неделям. Причем из общего числа заболевших необходимо исключать лиц, заразившихся в результате воздействия случайных факторов. В 1974 г. Д.А.Селидовкин с соавторами предложил использовать метод Вальда для эпидемиологических наблюдений и адаптировал его для этого. План слежения за инфекционной заболеваемостью, построенный с помощью метода Вальда, представляет собой графическое изображение нарастающего итога контрольных уровней заболеваемости по дням (рис. 28), где на оси абсцисс отмечается временной интервал (в днях) контрольного месяца, на оси ординат – число заболеваний (по данным первичной регистрации) в те же дни. Верхний и нижний контрольные уровни на плане-графике изображаются в виде двух восходящих в сторону последнего дня месяца почти параллельных линий. Первая из них (К1) является верхней границей доверительного интервала среднедневного числа заболеваний (уровень доверия 95%), полученного в результате многолетних наблюдений для каждого дня конкретного месяца, вторая (К2) символизирует нижнюю его границу. Эти линии делят поле прямоугольных координат на 3 зоны: верхнюю (зона неблагополучного эпидемического состояния - эпидемическая вспышка), среднюю (зона типичной для данной территории посуточной динамики спорадической заболеваемости) и нижнюю (зона благополучного эпидемического состояния). Ширина поля между линиями и угол их наклона к оси ординат зависят от вариабельности среднемноголетнего числа зарегистрированных спорадических заболеваний и интенсивности нарастания их количества в течение конкретного месяца. Под полем прямоугольных координат располагаются 2 строки, разделенные на ячейки, соответствующие интервалам оси абсцисс (см. рис. 28 – дни). В первой строке (К’) записывают в процессе слежения количество зарегистрированных заболеваний в текущие сутки, во второй – ежедневно нарастающее количество заболеваний, начиная с первого дня месяца Слежение за заболеваемостью ведется путем ежедневного нанесения на поле графика координат, соответствующих количеству заболеваний, зарегистрированных с начала месяца. Точки, соответствующие уровню ежедневной заболеваемости в виде нарастающего итога, последовательно соединяют линией. Для нанесения на график восходящих линий, отражающих границы обычного уровня заболеваемости, определяют 4 точки - по 2 для каждой линии. Начальные точки каждой линии символизируют предельно возможные уровни (верхний и нижний) заболеваемости первого числа конкретного месяца, конечные - соответственно максимальную и минимальную суммы заболеваний, зарегистрированных за месяц. Координаты этих точек вычисляют по формулам, предложенным Вальдом и адаптированным для построения плана-графика слежения за заболеваемостью. К 1 =
К 2 = где К 1 и К 2 – соответственно максимальный и минимальный контрольные уровни заболеваемости для первого дня месяца; К/ 1 и К/ 2 – соответственно максимальный и минимальный контрольные уровни заболеваемости для последнего дня месяца; 2,197 – постоянная величина; Ку – контрольный уровень заболеваемости, рассчитанный по многолетним данным; М – верхняя граница доверительного интервала среднемесячного числа заболеваний по многолетним данным с достоверностью 95%; 30 (31,28) – число дней в анализируемом месяце. Уровни К 1 и К 2 в приведенных формулах различаются знаками константы 2,197 (первый – со знаком плюс, второй – со знаком минус). Рассмотрим пример оперативного слежения за заболеваемостью с помощью метода Вальда. Рассчитаем контрольные уровни заболеваемости корью в городе М. на январь 2000 г., исходя из абсолютных ее показателей за тот же месяц в 1995-1999 гг. (табл. 34). Для этого выполним следующие этапы вычислений и запишем их в виде таблицы (см. табл. 34). Вначале определим верхнюю границу доверительного интервала среднего месячного числа заболеваний с достоверностью 95% (М) по формуле:
где Кi – сумма зарегистрированных заболеваний в исследуемом месяце за предшествующие годы; n – число лет наблюдения; r – коэффициент для расчета верхней доверительной границы среднемесячного числа заболеваний (определяется по таблице; см. приложение 8). В нашем примере сумма заболеваний, зарегистрированных в январе за 5 лет, равна 43. Наиболее близкое к ней значение
Таблица 34
|

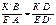
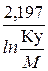 +
+ 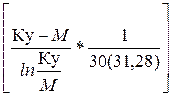 ;
; ;
;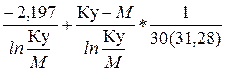 ;
;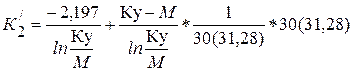 ,
,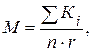
 в таблице для определения коэффициента r (см. приложение 8) – 40, поэтому коэффициент r для января равен 0,79, соответственно
в таблице для определения коэффициента r (см. приложение 8) – 40, поэтому коэффициент r для января равен 0,79, соответственно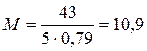 .
.


