Явища переносуПоширення молекул домішки в рідині або газі від місця її введення за відсутності макроскопічних переміщень в рідині або газі називається дифузією. Виникнення сили тертя між двома шарами рідини або газу, що рухаються з різними швидкостями, є проявом внутрішнього тертя або в'язкості. Перехід енергії від більш нагрітих областей до холодних за відсутності перемішування рідини або газу і конвекційних течій в них називається теплопровідністю. Внутрішній механізм цих трьох явищ – один, це хаотичний тепловий рух молекул, що проводить до їх перемішування. Ці явища називаються явищами переносу, оскільки при дифузії здійснюється перенесення речовини домішки, при внутрішньому терті - перенесення імпульсу (кількості руху), а при теплопровідності - перенесення кількості теплоти. Явища переносу - особливі незворотні процеси, в результаті яких відбувається перенесення маси, імпульсу і енергії. Середня довжина вільного пробігу і число зіткнень за секунду молекул газу. Для характеристики теплового руху в газах у багатьох випадках дуже важливо знати величину середнього вільного пробігу молекул λ;, тобто середню довжину шляху молекули між двома зіткненнями і середнє число зіткнень z однієї молекули за 1 секунду. Молекули газу, знаходячись в тепловому русі, безперервно стикаються одна з одною. Мінімальна відстань, на яку зближуються при зіткненні центри двох молекул, називається ефективним діаметром молекули d. Визначити середню довжину шляху молекули між двома зіткнення. Припустимо, що усі молекули, окрім даної, покояться. Молекула, що рухається, зіткнеться впродовж часу z=nπ d2vср.
Рисунок. 2.34. Насправді середнє число зіткнень має бути більше отриманої величини, так, як внаслідок руху інших молекул дана молекула отримала б деяке число зіткнень навіть у тому випадку, якщо б вона залишалася нерухомою. Точний підрахунок показує, що отриманий результат має бути помножений на z= а середня довжина вільного пробігу молекул дорівнює:
Середня довжина вільного пробігу молекул газу за нормальних умов становить Дифузія. Якщо уздовж будь-якого напряму (наприклад уздовж осі Х) існує неоднорідність
В такому не врівноваженому стані відбувається перенесення (дифузія) маси газу. Закон дифузії був отриманий німецьким фізиком Фіком. Цей закон виражається формулою.
де jm - густина потоку маси дифундуючої речовини, що проходить в одиницю часу через одиничний майданчик, перпендикулярний осі Х. Знак мінус показує, що перенесення маси відбувається у напрямі убування густини. У загальнішому вигляді закон Фіка може бути виражений формулою:
Маса дифундуючої речовини δ m пропорційна часу dt, площі dS і градієнту густини D - коефіцієнт дифузії. Коефіцієнт дифузії чисельно дорівнює масі дифундуючої речовини, що пройшла через одиницю площі за одиницю часу при градієнті густини, рівному одиниці.
(2.22)
Для різних газів за нормальних умов коефіцієнт дифузії має значення приблизно від 10-5 до 10-4 м2/с. Так, як середня швидкість vср пропорційна Теплопровідність Дослідним шляхом встановлено, якщо в якомусь середовищі уздовж деякого напряму Х температура не залишається постійною, то уздовж цього напряму встановлюється потік тепла. У загальному випадку повну характеристику зміни температури уздовж напряму Х отримаємо, якщо знатимемо швидкість зміни температури або градієнт температури уздовж осі Х:
Відмітимо, що температура скалярна величина, але градієнт температури це вектор, спрямований у бік збільшення температури. Користуючись поняттям про градієнт температури, можна написати рівняння теплопровідності:
Де JE - густина теплового потоку - енергія, яка переноситься у формі теплоти в одиницю часу через одиничний майданчик, c - коефіцієнт теплопровідності. Знак мінус показує, що потік енергії має напрям, протилежний до напряму градієнта температури.
. (2.24)
Коефіцієнт теплопровідності може бути визначений як кількість тепла, яке протікає через одиницю площі за одиницю часу при градієнті температури рівному одиниці. Речовини, для яких коефіцієнт теплопровідності має велике значення, називають хорошими провідниками теплоти, а ті, для яких χ має малі значення, - поганими провідниками тепла. Кращими провідниками є метали, гірше проводять дерево, скло, рослинні тканини. Поганими провідниками тепла є гази і рідини (за винятком рідких металів). Згідно кінетичної теорії газів коефіцієнт теплопровідності рівний:
де r - густина газу, сv - питома теплоємність газу при постійному об'ємі. Внутрішнє тертя (в'язкість) Механізм виникнення внутрішнього тертя між паралельними шарами газу або рідини, які рухаються з різними швидкостями, полягає в тому, що із-за хаотичного теплового руху відбувається обмін молекулами між шарами. Внаслідок чого імпульс шару, що рухається швидше, зменшується і навпаки, імпульс шару молекул, які рухаються повільніше збільшується. Це призводить до гальмування шару, який рухається швидше і прискоренню шару, який рухається повільніше.
(2.26)
- градієнт швидкості. Знак мінус вказує, що сили внутрішнього тертя, мають такий напрям, що шар газу, який рухається швидко, гальмується, а шар, який рухається повільніше, прискорюється. Згідно кінетичної теорії газів коефіцієнт внутрішнього тертя рівний:
де - ρ - густина газу, vср - середня арифметична швидкість молекул газу, де λ - середня довжина вільного пробігу. Явища дифузії, в'язкості і теплопровідності мають немало спільного. По-перше, усі ці явища обумовлюються перенесенням тієї або іншої величини: явища дифузії - перенесенням маси, явища теплопровідності - перенесенням енергії, явища в'язкості - перенесенням імпульсу. По-друге, усі ці явища супроводжуються розсіянням енергії. По-третє, в механізмі усіх цих явищ грає велику роль середня довжина вільного пробігу молекул. Зіставлення явищ дифузії, внутрішнього тертя і теплопровідності приводиться в таблиці 2.4 Таблиця 2.4
Питання і завдання: 1. Як називаються газові процеси, які проходять при постійній температурі, об'ємі, тиску? 2. Накреслити і пояснити графіки ізотермічного і ізобарного процесів в координатах p, V; p, T; T, V. 3. У чому зміст і яка мета виведення основного рівняння молекулярно-кінетичної теорії газів? 4. Який фізичний зміст має функція розподілу молекул за швидкостями? 5. У чому суть розподілу Больцмана? 6. Як міняється атмосферний тиск з висотою? 7. Що таке середня довжина вільного пробігу молекул газу. Від чого вона залежить? 8. Які явища переносу ви знаєте? У чому їх суть і за яких умов вони виникають? 9. Балон містить 2 кг газу при 300 К. Яку масу газу треба видалити з балона, щоб при нагріванні до 400 К тиск залишився тим самим? (0, 5 кг). 10. Тиск повітря в шинах велосипеда при температурі 12°С дорівнює 1, 5·105Па. Яким став тиск при 31°С? (1, 6·105 Па). 11. Скільки молекул міститься в 1 м3 повітря за нормальних умов? (2, 65·1025 молекул). 12. Густина повітря за нормальних умов дорівнює 1, 3 кг/м3. Якою буде густина повітря при температурі 100°С і тиску 4·105Н/м2? (3, 8 кг/м3). 13. У балоні, при температурі 20°С знаходиться суміш газів 200 г водню і 100 г азоту під тиском 2 атмосфери. Знайти густину суміші.(0, 23кг/ м3). 14. Балон, що містить 1, 67 кг гелію, розірвався при температурі 400° C. Яка максимальна маса азоту може зберігатися в цьому балоні при температурі 30°С і при п'ятикратному запасі міцності. (5, 2 кг). 15. Визначити найбільш ймовірну, середню квадратичну і середню арифметичну швидкість молекул газу, густина якого при тиску 40 кПа, дорівнює 0, 35 кг/м3.(478 м/с, 586 м/с, 540 м/с). 16. На якій висоті густина повітря в два рази менше густини на рівні моря. Температуру вважати постійною і рівною 0°С.(5, 5 км). 17. Знайти атмосферний тиск на висоті 10 км над рівнем моря. Вважати температуру постійною і рівною 0°С, а Р0= 1 ат. (0, 285 ат). 18. Визначити середню довжину вільного пробігу і число зіткнень молекул водню за одну секунду при температурі 300 К і тиском 5 кПа. Ефективний діаметр молекул прийняти рівним 0, 28 нм. (2, 38·10-6м). 19. Коефіцієнти дифузії і внутрішнього тертя за деяких умов дорівнюють 1.42·10-4 м2/с і 8, 5 мкПа·с. Визначити концентрацію молекул повітря за цих умов.(1, 25·1024 м-1). Тема 7 Перший закон термодинаміки Термодинаміка - це наука про теплові явища. В протилежність молекулярно-кінетичній теорії, яка робить висновки на основі уявлень про молекулярну будову речовини, термодинаміка виходить з найбільш загальних закономірностей теплових процесів і властивостей макроскопічних систем. Висновки термодинаміки спираються на сукупність дослідних фактів і не залежать від наших знань про внутрішній устрій речовини, хоча у цілому ряді випадків термодинаміка використовує молекулярно-кінетичні моделі для ілюстрації своїх висновків. Термодинаміка розглядає ізольовані системи тіл, що знаходяться в стані термодинамічної рівноваги. Це означає, що в таких системах припинилися усі спостережувані макроскопічні процеси. Важливою властивістю термодинамічно-рівноважної системи являється вирівнювання температури усіх її частин. Якщо термодинамічна система була виведена із стану рівноваги зовнішніми діями, то зрештою вона перейде в інший рівноважний стан. Такий перехід називається термодинамічним процесом. Якщо процес протікає досить повільно (у межі нескінченно повільно), то система в кожен момент часу виявляється близькою до рівноважного стану. Процеси, що складаються з послідовності рівноважних станів, називаються квазістатичними. § 30. Внутрішня енергія Одним з найважливіших понять термодинаміки є внутрішня енергія тіла. Усі макроскопічні тіла мають енергію, яка знаходиться усередині самих тіл. З точки зору молекулярно-кінетичної теорії внутрішня енергія речовини складається з кінетичної енергії усіх атомів і молекул і потенціальної енергії їх взаємодії. Зокрема, внутрішня енергія ідеального газу дорівнює сумі кінетичних енергій усіх молекул газу, що знаходяться в безперервному і безладному тепловому русі. Внутрішня енергія ідеального газу залежить тільки від його температури і не залежить від об'єму. Під числом ступенів свободи i розуміють число незалежних рухів (чи координат, які визначають положення частки в просторі). У одноатомних газів (аргон, гелій і так далі) кожна молекула може мати три незалежні рухи уздовж трьох взаємно перпендикулярних осей. Таким чином, одноатомна молекула має три ступені свободи (i =3). Молекула двоатомного газу (H2, N2, CO та ін.) має п'ять ступенів свободи (i =5), оскільки окрім трьох поступальних рухів вона може мати два обертальні рухи навколо двох взаємно перпендикулярних осей, що становлять прямий кут з лінією, що сполучає обидва атоми.
Рисунок 2.35. На рисунку 2.35 зображена модель двоатомної молекули. Молекула може здійснювати п'ять незалежних рухів: три поступальних ходи уздовж осей X, Y, Z і два обертання відносно осей X і Y. Молекули трьохатомного газу мають шість ступенів свободи (i =6): (3 поступальні і 3 обертальні). Ці ж шість ступенів свободи властиві кожній молекулі, що містить більше трьох атомів. У класичній статистичній фізиці доводиться теорема про рівномірний розподіл енергії по ступенях свободи (закон Больцмана): Якщо система молекул знаходиться в тепловій рівновазі при температурі T, то середня кінетична енергія рівномірно розподілена між усіма ступенями свободи і для кожного ступеня свободи молекули вона рівна
Тоді середня кінетична енергія однієї молекули рівна:
Оскільки молекула будь-якого газу має три поступальні ступені свободи середня поступальна енергія будь-якої молекули рівна:
Цей результат ми знаходили виходячи з основного рівняння МКТ. Отримаємо вираз для молекулярно-кінетичної або внутрішньої енергії газу:
Таким чином, внутрішня енергія U тіла однозначно визначається макроскопічними параметрами, що характеризують стан тіла. Вона не залежить від того, яким чином було реалізовано цей стан. Прийнято говорити, що внутрішня енергія є функцією стану. § 31. Перший закон термодинаміки Способи зміни внутрішньої енергії Внутрішня енергія тіла не є постійною величиною: у одного і того ж тіла вона може змінюватися. При підвищенні температури внутрішня енергія тіла збільшується, так, як збільшується середня швидкість руху молекул. З пониженням температури внутрішня енергія зменшується. Зміна внутрішньої енергії ідеального газу дорівнює:
Якими ж способами можна збільшити або зменшити швидкість молекул? Якщо зовнішня дія на систему носить механічний характер, то зміна енергії визначається роботою A΄ зовнішніх сил, діючих на систему. Отже, внутрішню енергію тіла можна збільшити, здійснюючи роботу над тілом. Якщо газ піддається стискуванню в циліндрі під поршнем, то зовнішні сили здійснюють над газом деяку роботу A'. В той же час сили тиску, діючі з боку газу на поршень, здійснюють роботу A = - A'. Якщо об'єм газу змінився на малу величину Δ V, то елементарна робота, здійснена газом дорівнює: Δ А=FΔ x= pSΔ x = pΔ V де p - тиск газу, S - площа поршня, Δ x - переміщення поршня, Δ V=SΔ x. При розширенні робота, що здійснюється газом, позитивна, при стискуванні - негативна. У загальному випадку при переході з деякого початкового стану (1) в кінцевий стан (2) робота газу виражається формулою:
чи в межі при Δ V → 0:
Рисунок 2.36. Робота чисельно дорівнює площі під графіком процесу на діаграмі (p, V) (рис. 2.36). Величина роботи залежить від того, яким чином здійснювався перехід з початкового стану в кінцевий. На рисунку 2.37 зображено три різні процеси, що переводять газ із стану (1) в стан (2). У усіх трьох випадках газ здійснює різну роботу.
Рисунок 2.37. У тому випадку, якщо розширення газу проходить при постійному тиску роботу можна розрахувати по формулі: р =const, А= рΔ V. (2.34) У випадку, корду процес проходить при постійному об'ємі газ не виконує роботи. V=const, А=0. (2.35) Отримаємо формулу роботи ідеального газу при ізотермічному розширенні: При Т=const,
Внутрішня енергія тіла може змінюватися не лише в результаті здійснюваної роботи, але і внаслідок теплообміну. При тепловому контакті тіл внутрішня енергія одного з них може збільшуватися, а внутрішня енергія іншого - зменшуватися. В цьому випадку говорять про тепловий потік від одного тіла до іншого. Кількістю теплоти, отриманої тілом, називають зміну внутрішньої енергії тіла в результаті теплообміну. Кількість теплоти є енергетичною величиною. У СІ кількість теплоти позначається буквою Q і вимірюється в одиницях механічної роботи - джоулях (Дж). Процес зміни внутрішньої енергії, при якій над тілом не здійснюється робота, а енергія передається від одних часток до інших, називають теплопередачею. Таким чином зміна внутрішньої енергії системи ∆ U під час процесу переходу з початкового стану в кінцевий дорівнює сумі виконаної зовнішніми тілами роботи А΄ і отриманої системою кількості теплоти Q. ∆ U=U2 - U1=A΄ + Q. (2.37) Цей вираз називається першим законом (початком) термодинаміки. Так, як робота зовнішніх сил А΄ =-А, де А - робота розширення газу, перший закон термодинаміки можна сформулювати таким чином: Кількість теплоти, що передається газу, витрачається на зміну його внутрішньої енергії і на виконання роботи проти зовнішніх сил. Q =A + ∆ U. (2.38) Рівняння першого закону термодинаміки в диференціальній формі має вигляд δ Q = dU +δ A. (2.39) У цьому виразі dU є повним диференціалом, а δ A і δ Q такими не являються. § 32. Теплоємність Теплоємністю називають кількість теплоти, яка необхідна для нагрівання тіла на Питома теплоємність речовини - величина рівна кількості теплоти, яка необхідна для нагрівання 1 кг речовини на 1 К
Одиниця питомої теплоємності (Дж/(кг·К) Молярна теплоємність - величина рівна кількості теплоти, яка необхідна для нагрівання 1 моля речовини на 1 К
Одиниця молярної теплоємності (Дж/(моль·К). Питома теплоємність пов'язана з молярною співвідношенням: Cm=c·M. (2.42) Розрізняють молярні теплоємності при сталому об'ємі і сталому тиску Cv і Cp
Порівнюючи теплоємності Cv і Cp отримаємо: СР=Сv+R. (2.45) Цей вираз називається рівнянням Майєра. З нього виходить, що Ср завжди більша за Сv на величину універсальної газової сталої R. З цього можна визначити фізичний зміст універсальної газової сталої R. Вона чисельно дорівнює роботі ізобарного розширення одного моля ідеального газу при нагріванні його на 1°. При розгляді термодинамічних процесів важливо знати характерне для кожного газу відношення Ср до Сv:
Згідно класичної теорії, теплоємність газів не залежить від температури проте дослід доводить, що це не так.
Рисунок 2.38. На рисунку 2.38. показана експериментальна залежність Сv для водню. Вивчення цієї залежності показує, що в температурних інтервалах DТ1, DТ2, DТ3 теплоємність не залежить від температури, але в цілому збільшується з підвищенням температури. Такий хід залежності можна пояснити, відмовившись від закону про рівномірний розподіл енергії за ступенями свободи молекул. Можна припустити, що число ступенів свободи збільшується з підвищенням температури. При низьких температурах (DТ1) енергія розподіляється тільки між ступенями свободи поступального руху Сv = 3R/2. При середніх температурах (DТ2) молекули починають обертатися Сv = 5R/2. При подальшому підвищенні температури " збуджуються" і ступені свободи коливального руху. При високих температурах (DТ3) Сv = 7R/2. Неточність закону про рівномірний розподіл енергії по ступенях свободи молекул пояснюється тим, що рух молекул не підпорядковується законам класичної механіки і класичної статистики. Залежність Сv від Т пояснює квантова теорія теплоємкостей. § 33. Перший закон термодинаміки для різних термодинамічних процесів Розглянемо перший початок термодинаміки для ізопроцесів. Якщо термодинамічний процес відбувається при постійній температурі T=const (ізотермічний процес) внутрішня енергія газу не змінюється. Тоді кількість теплоти, що передається газу витрачається на виконання роботи проти зовнішніх сил. ∆ U =0, Q = А, Якщо термодинамічний процес відбувається під постійним тиском P=const Q = ∆ U+ А. (2.48) Цей вираз можна представити у такому вигляді:
з останнього виразу слідує, що при ізобарному процесі
При ізобарному розширенні Q > 0 - тепло поглинається газом, і газ здійснює позитивну роботу. При ізобарному стисканні Q < 0 - тепло віддається зовнішнім тілам. В цьому випадку A< 0. Температура газу при ізобарному стисканні зменшується, T2 < T1; внутрішня енергія убуває, Δ U < 0.
А =0, Q = ∆ U, (2.49) Кількість теплоти Q, отримана газом в процесі ізотермічного розширення, перетворюється на роботу над зовнішніми тілами. При ізотермічному стисканні робота зовнішніх сил, проведена над газом, перетворюється на тепло, яке передається навколишнім тілам. § 34. Адіабатичний процес Разом з ізохорним, ізобарним і ізотермічним процесами в термодинаміці розглядаються процеси, що протікають у відсутність теплообміну з навколишніми тілами. Посудини з теплонепроникними стінками називаються адіабатичними оболонками, а процеси розширення або стискання газу в таких посудинах називаються адіабатичними. У адіабатичному процесі Q = 0; тому перший закон термодинаміки набуває вигляду A=-Δ U, (2.50) тобто газ здійснює роботу за рахунок спаду своєї внутрішньої енергії. Запишемо це рівняння в диференціальному виді: δ А= - dU або PdV = -ν Cv dT. (2.51) Продиференціювавши рівняння стану ідеального газу отримаємо: PdV+VdP=ν RdT. (2.52) Розділимо рівняння (2.52) на (2.51)
Інтегруючи цей вираз в межах від V1 до V2 відповідно від Р1 до Р2 і після потенціювання, отримаємо:
Отриманий вираз є рівняння адіабатичного процесу. Ці рівняння називають рівнянням Пуассона. На площині (Р, V) процес адіабатичного розширення (чи стискання) газу зображується кривою, яка називається адіабатою. При адіабатичному розширенні газ здійснює позитивну роботу (A > 0); тому його внутрішня енергія зменшується (Δ U < 0). Це призводить до зниження температури газу. Внаслідок цього тиск газу при адіабатичному розширенні убуває швидше, ніж при ізотермічному розширенні (рис. 2.39).
Рисунок 2.39. Сімейства ізотерм (червоні криві) і адіабат (сині криві) ідеального газу. Використовуючи рівняння Менделєєва-Клапейрона, можна рівняння Пуассона записати з параметрами Р і Т
Розрахуємо роботу, що здійснюється газом при адіабатичному процесі. δ А=- dU=- ν Cv dT, А= ν Cv (T1 -Т2). (2.55) Використовуючи рівняння Пуассона вираз (2.55) можна записати у виді:
Перший закон (початок) термодинаміки є узагальненням закону збереження і перетворення енергії для термодинамічної системи. Згідно з цим законом, енергія не може бути створена або знищена; вона передається від однієї системи до іншої і перетворюється з однієї форми в іншу. Важливим наслідком першого закону термодинаміки є твердження про неможливість створення машини, здатної здійснювати корисну роботу без споживання енергії ззовні і без яких-небудь змін усередині самої машини. Така гіпотетична машина дістала назву вічного двигуна (perpetum mobile) першого роду. Численні спроби створити таку машину незмінно закінчувалися провалом. Будь-яка машина може здійснювати позитивну роботу A над зовнішніми тілами тільки за рахунок отримання деякої кількості теплоти Q від навколишніх тіл або зменшення Δ U своєї внутрішньої енергії. Приклади розв’язку задачі. Кисень масою m =2 кг займає об'єм V1 = 1 м3 і знаходиться під тиском p1 = 0, 2 МПа. Газ був нагрітий спочатку при постійному тиску до об'єму V2 = 3 м3, а потім при постійному об'ємі до тиску p3 = 0, 5 МПа. Знайти: 1) зміну внутрішньої енергії ∆ U газу; 2) виконану ним роботу A 3) кількість теплоти Q, передану газу. Побудувати графік процесу.
Питання і задачі: 1. Що таке внутрішня енергія ідеального газу? Якими параметрами вона визначається. В результаті яких процесів вона може зміняться? 2. Що називається числом ступенів свободи молекул газу? 3. При якому процесі уся кількість теплоти, отримана газом, витрачається на збільшення внутрішньої енергії газу? 4. При якому процесі уся кількість теплоти, отримана газом, витрачається на виконання роботи проти зовнішніх сил? 5. Який газовий процес називається адіабатним? Сформулюйте перший початок термодинаміки для цього процесу. Наведіть приклади таких процесів. 6. Що таке питома і молярна теплоємності? Як розрахувати молярні теплоємності газу? 7. При ізобарному нагріванні одноатомний газ виконав роботу 139, 67 Дж. Знайти зміну його внутрішньої енергії. (209, 5 Дж). 8. При здійсненні газом роботи, рівної 1000 Дж, йому було передано 1500 Дж теплоти. На скільки збільшилася внутрішня енергія газу? (500 Дж). 9. При ізобарному розширенні ідеального газу, в процесі якого здійснена робота 10. Один моль одноатомного газу нагрівається при постійному тиску. Яку кількість теплоти необхідно передати газу, щоб його об'єм подвоївся? Початкова температура газу 0°С. (5672 Дж). 11. Гелій масою m = 1 г був нагрітий на ∆ T = 100 К при сталому тиску р. Визначити: 12. Яка доля ω 1 кількості теплоти Q1, що підводиться до ідеального газу при ізобарному процесі, витрачається на збільшення ∆ U внутрішньої енергії газу і яка доля ω 2 - витрачається на роботу А розширення? Розглянути три випадки, якщо газ: 1) одноатомний; 2) двоатомний; 3) трьохатомний. (0, 4; 0, 29; 0, 25) 13. У циліндрі під поршнем знаходиться водень масою m = 0, 02 кг при температурі 14. Горюча суміш в двигуні дизеля запалюється при температурі Т2 = 1, 1 кК. Початкова температура суміші T1 = 350 К. У скільки разів треба зменшити об'єм суміші при стискуванні, щоб вона запалилася? Стискання вважати адіабатним. Показник адіабати γ для суміші прийняти рівним 1, 4. (1, 75) Тема 8 Другий закон термодинаміки § 35. Теплові двигуни. Термодинамічні цикли. Цикл Карно Тепловим двигуном називається пристрій, здатний перетворювати отриману теплову енергію на механічну роботу. Механічна робота в теплових двигунах виконується в процесі розширення деякої речовини, яке називається робочим тілом. В якості робочого тіла зазвичай використовуються газоподібні речовини (пари бензину, повітря, водяна пара). Робоче тіло отримує теплову енергію в процесі теплообміну з тілами, що мають великий запас внутрішньої енергії. Ці тіла називаються тепловими резервуарами. Як випливає з першого закону термодинаміки, отримана газом кількість теплоти Q повністю перетворюється на роботу A при ізотермічному процесі, при якому внутрішня енергія залишається незмінною (Δ U = 0),: A = Q. Але такий одноразовий акт перетворення теплоти в роботу не представляє інтересу для техніки. Реально існуючі теплові двигуни (парові машини, двигуни внутрішнього згорання і т. д.) працюють циклічно. Процес теплопередачі і перетворення отриманої кількості теплоти в роботу періодично повторюється. Для цього робоче тіло повинне здійснювати круговий процес або термодинамічний цикл, при якому періодично відновлюється початковий стан. Кругові процеси зображуються на діаграмі (p, V) газоподібного робочого тіла за допомогою замкнутих кривих (рис. 2.40). При розширенні газ здійснює позитивну роботу A1, рівну площі під кривою abc, при стисканні газ здійснює негативну роботу A2, рівну по модулю площі під кривою cda. Повна робота за цикл A = A1 + A2 на діаграмі (p, V) дорівнює площі циклу. Робота A позитивна, якщо цикл обходиться за годинниковою стрілкою, і A негативна, якщо цикл обходиться в протилежному напрямі.
Рисунок 2.40. Загальна властивість усіх кругових процесів полягає в тому, що їх неможливо провести, приводячи робоче тіло в тепловий контакт тільки з одним тепловим резервуаром. Їх треба, принаймні, два. Тепловий резервуар з вищою температурою називають нагрівачем, а з нижчою - холодильником. Здійснюючи круговий процес, робоче тіло отримує від нагрівача деяку кількість теплоти Q1 > 0 і віддає холодильнику кількість теплоти Q2 < 0. Повна кількість теплоти Q, отримана робочим тілом за цикл, дорівнює: Q = Q1 - Q2. (2.57) При обході циклу робоче тіло повертається в початковий стан, отже, зміна його внутрішньої енергії дорівнює нулю (Δ U = 0). Згідно з першим законом термодинаміки, Δ U=Q - A= 0. (2.58) Звідси слідує: A = Q = Q1 - Q2. (2.59) Робота A, що здійснюється робочим тілом за цикл, дорівнює отриманій за цикл кількості теплоти Q. Відношення роботи A до кількості теплоти Q1, отриманої робочим тілом за цикл від нагрівача, називається коефіцієнтом корисної дії η теплової машини:
Коефіцієнт корисної дії вказує, яка частина теплової енергії, отриманої робочим тілом від " гарячого" теплового резервуару, перетворилася на корисну роботу. Інша частина (1 - η) була " марно" передана холодильнику. Коефіцієнт корисної дії тепло
|


 , тоді
, тоді (2.19)
(2.19)
 (2.20)
(2.20) (2.21)
(2.21) Згідно кінетичної теорії газів.
Згідно кінетичної теорії газів. , то при збільшенні температури швидкість дифузії збільшується.
, то при збільшенні температури швидкість дифузії збільшується.
 (2.23)
(2.23) Точний підрахунок явищ теплопровідності проводиться на основі закону Фур'є: кількість тепла δ Q, що проходить за проміжок часу dt через елементарний майданчик dS, перпендикулярний лінії, уздовж якої тече потік енергії, пропорційний часу dt, площі dS і градієнту температури
Точний підрахунок явищ теплопровідності проводиться на основі закону Фур'є: кількість тепла δ Q, що проходить за проміжок часу dt через елементарний майданчик dS, перпендикулярний лінії, уздовж якої тече потік енергії, пропорційний часу dt, площі dS і градієнту температури  .
. (2.25)
(2.25) Сила внутрішнього тертя між двома шарами газу (чи рідини) описується законом Ньютона.
Сила внутрішнього тертя між двома шарами газу (чи рідини) описується законом Ньютона. де h - коефіцієнт внутрішнього тертя (динамічна в'язкість).
де h - коефіцієнт внутрішнього тертя (динамічна в'язкість). (2.27)
(2.27)


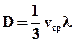



 (2.28)
(2.28) (2.29)
(2.29) (2.30)
(2.30) (2.31)
(2.31) (2.32)
(2.32)
 (2.33)
(2.33)

 , оскільки
, оскільки  отримаємо:
отримаємо: (2.36)
(2.36)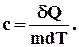 (2.40)
(2.40) (2.41)
(2.41) (2.43)
(2.43)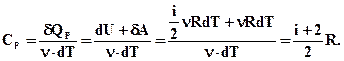 (2.44)
(2.44) (2.46)
(2.46)

 (2.47)
(2.47)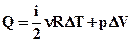 , але
, але 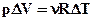 , тоді
, тоді

 Якщо термодинамічний процес відбувається при постійному об'ємі V=const (ізохорний процес), тоді:
Якщо термодинамічний процес відбувається при постійному об'ємі V=const (ізохорний процес), тоді:
 чи
чи 
 (2.53)
(2.53)
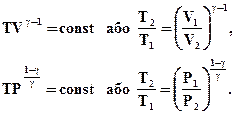 (2.54)
(2.54) (2.56)
(2.56)
 p3 = 0, 5 МПа
∆ U -? A-? Q-?
p3 = 0, 5 МПа
∆ U -? A-? Q-?
 де Δ Т=(Т3-Т1)
З рівнянь (1) і (3) знайдемо Т1 і Т3, і враховуючи, що i=5, знайдемо ∆ U
де Δ Т=(Т3-Т1)
З рівнянь (1) і (3) знайдемо Т1 і Т3, і враховуючи, що i=5, знайдемо ∆ U

 Робота А дорівнює роботі ізобарного розширення А1, 2 =Р1(V2 - V1), оскільки на ділянці (2-3) V=const і робота дорівнює нулю.
А =Р1(V2 - V1)= 0, 4·106 Дж.
Робота А дорівнює роботі ізобарного розширення А1, 2 =Р1(V2 - V1), оскільки на ділянці (2-3) V=const і робота дорівнює нулю.
А =Р1(V2 - V1)= 0, 4·106 Дж.  Кількість теплоти Q=Δ U+A=3, 65·106 Дж.
V(м3)
Кількість теплоти Q=Δ U+A=3, 65·106 Дж.
V(м3)

 (2.60)
(2.60)


