Рассмотрим кратко величины, вводимые для описания затухающих колебаний.
1.Критическое сопротивление контура  (критический коэффициент сопротивления среды
(критический коэффициент сопротивления среды  ). Критическое сопротивление контура – это такое сопротивление, при котором в контуре начинается апериодический разряд. В этом случае колебания в контуре отсутствуют, заряд на обкладках конденсатора убывает монотонно до нуля (кривая 1 на рис. 5.16), или, пройдя один раз положение равновесия, заряд конденсатора в итоге монотонно будет убывать до нуля (кривая 2 на рис. 5.16).
). Критическое сопротивление контура – это такое сопротивление, при котором в контуре начинается апериодический разряд. В этом случае колебания в контуре отсутствуют, заряд на обкладках конденсатора убывает монотонно до нуля (кривая 1 на рис. 5.16), или, пройдя один раз положение равновесия, заряд конденсатора в итоге монотонно будет убывать до нуля (кривая 2 на рис. 5.16).
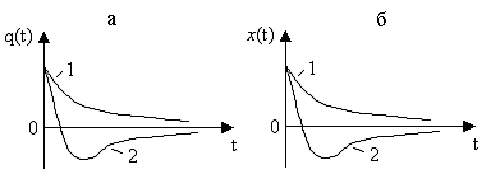
Рис. 5.16
Убывание заряда 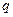 , смещения
, смещения 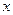 тела в механической системе по кривым 1 или 2, либо по кривой, расположенной между ними, зависит от начальных условий. Например, если поместить физический маятник в жидкую вязкую среду и, отклонив его от положения равновесия, отпустить без начальной скорости, то тогда смещение
тела в механической системе по кривым 1 или 2, либо по кривой, расположенной между ними, зависит от начальных условий. Например, если поместить физический маятник в жидкую вязкую среду и, отклонив его от положения равновесия, отпустить без начальной скорости, то тогда смещение  маятника будет изменяться по кривой 1 (рис. 5.16, б). Если же отпустить маятник с начальной скоростью, направленной к положению равновесия, то тогда его смещение может со временем изменяться по кривой 2 (рис. 5.16, б), т.е. он пройдет один раз положение равновесия, затем отклонится, и после этого в итоге будет монотонно приближаться к положению равновесия.
маятника будет изменяться по кривой 1 (рис. 5.16, б). Если же отпустить маятник с начальной скоростью, направленной к положению равновесия, то тогда его смещение может со временем изменяться по кривой 2 (рис. 5.16, б), т.е. он пройдет один раз положение равновесия, затем отклонится, и после этого в итоге будет монотонно приближаться к положению равновесия.
Выведем формулу для критического сопротивления контура  через параметры контура L и C. При увеличении сопротивления
через параметры контура L и C. При увеличении сопротивления  угловая частота затухающих колебаний будет уменьшаться, а период колебаний ТЗ будет возрастать, и для сопротивления
угловая частота затухающих колебаний будет уменьшаться, а период колебаний ТЗ будет возрастать, и для сопротивления  , равного
, равного  , можно записать
, можно записать
 :
:  ,
,  ,
,
 . (5.51)
. (5.51)
Для  в контуре наблюдается апериодический разряд, а при
в контуре наблюдается апериодический разряд, а при  в контуре происходят затухающие колебания.
в контуре происходят затухающие колебания.
По таблице аналогий (см. табл. 5.1) для критического коэффициента сопротивления среды  можно записать (L® m, 1/С ® к)
можно записать (L® m, 1/С ® к)
 . (5.52)
. (5.52)
2. Время релаксации τ – это время, в течение которого амплитуда колебаний убывает в e раз (e -основание натурального логарифма):
 ,
, 
 . (5.53)
. (5.53)
За время релаксации в системе совершается Ne полных колебаний:
 (5.54)
(5.54)
3. Логарифмический декремент затухания δ равен натуральному логарифму отношения двух амплитуд, взятых через период:
 . (5.55)
. (5.55)
4. Добротность Q системы можно ввести как величину, определяющую потери энергии колебаний системы за один условный период колебаний,
 . (5.56)
. (5.56)
Полная энергия колебаний пропорциональна квадрату амплитуды колебаний и поэтому выражение (5.56) можно записать в следующем виде:
 . (5.57)
. (5.57)
Из формулы (5.56) следует, что чем выше добротность Q системы, тем медленнее в ней затухают колебания.
Приведем ориентировочные значения Q для различных систем:
1) колебательный контур на радиочастотах ( ~ 106 рад/с): Q ~ 100; 2) полый резонатор диапазона сверхвысоких частот (ω ~ 1011 рад/с): Q ~ 105; 3) камертон: Q ~ 104; 4) колебания кварцевой пластины: Q ~ 105; 5) излучение атома как колебательной системы: Q ~ 107.
~ 106 рад/с): Q ~ 100; 2) полый резонатор диапазона сверхвысоких частот (ω ~ 1011 рад/с): Q ~ 105; 3) камертон: Q ~ 104; 4) колебания кварцевой пластины: Q ~ 105; 5) излучение атома как колебательной системы: Q ~ 107.
Как видно, для применяемых на практике систем Q ³ 100, т.е. для них выполняются условия малого затухания:
 .
.
Тогда из формулы (5.57) получим ( )
)
 . (5.58)
. (5.58)
Для добротности механической системы и колебательного контура из формулы (5.58) в условиях малого затухания можно получить следующие формулы:
 ,
,  . (5.59)
. (5.59)

 (критический коэффициент сопротивления среды
(критический коэффициент сопротивления среды  ). Критическое сопротивление контура – это такое сопротивление, при котором в контуре начинается апериодический разряд. В этом случае колебания в контуре отсутствуют, заряд на обкладках конденсатора убывает монотонно до нуля (кривая 1 на рис. 5.16), или, пройдя один раз положение равновесия, заряд конденсатора в итоге монотонно будет убывать до нуля (кривая 2 на рис. 5.16).
). Критическое сопротивление контура – это такое сопротивление, при котором в контуре начинается апериодический разряд. В этом случае колебания в контуре отсутствуют, заряд на обкладках конденсатора убывает монотонно до нуля (кривая 1 на рис. 5.16), или, пройдя один раз положение равновесия, заряд конденсатора в итоге монотонно будет убывать до нуля (кривая 2 на рис. 5.16).
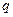 , смещения
, смещения 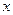 тела в механической системе по кривым 1 или 2, либо по кривой, расположенной между ними, зависит от начальных условий. Например, если поместить физический маятник в жидкую вязкую среду и, отклонив его от положения равновесия, отпустить без начальной скорости, то тогда смещение
тела в механической системе по кривым 1 или 2, либо по кривой, расположенной между ними, зависит от начальных условий. Например, если поместить физический маятник в жидкую вязкую среду и, отклонив его от положения равновесия, отпустить без начальной скорости, то тогда смещение  маятника будет изменяться по кривой 1 (рис. 5.16, б). Если же отпустить маятник с начальной скоростью, направленной к положению равновесия, то тогда его смещение может со временем изменяться по кривой 2 (рис. 5.16, б), т.е. он пройдет один раз положение равновесия, затем отклонится, и после этого в итоге будет монотонно приближаться к положению равновесия.
маятника будет изменяться по кривой 1 (рис. 5.16, б). Если же отпустить маятник с начальной скоростью, направленной к положению равновесия, то тогда его смещение может со временем изменяться по кривой 2 (рис. 5.16, б), т.е. он пройдет один раз положение равновесия, затем отклонится, и после этого в итоге будет монотонно приближаться к положению равновесия. угловая частота затухающих колебаний будет уменьшаться, а период колебаний ТЗ будет возрастать, и для сопротивления
угловая частота затухающих колебаний будет уменьшаться, а период колебаний ТЗ будет возрастать, и для сопротивления  :
:  ,
,  ,
, . (5.51)
. (5.51) в контуре наблюдается апериодический разряд, а при
в контуре наблюдается апериодический разряд, а при  в контуре происходят затухающие колебания.
в контуре происходят затухающие колебания. . (5.52)
. (5.52) ,
, 
 . (5.53)
. (5.53) (5.54)
(5.54) . (5.55)
. (5.55) . (5.56)
. (5.56) . (5.57)
. (5.57) ~ 106 рад/с): Q ~ 100; 2) полый резонатор диапазона сверхвысоких частот (ω ~ 1011 рад/с): Q ~ 105; 3) камертон: Q ~ 104; 4) колебания кварцевой пластины: Q ~ 105; 5) излучение атома как колебательной системы: Q ~ 107.
~ 106 рад/с): Q ~ 100; 2) полый резонатор диапазона сверхвысоких частот (ω ~ 1011 рад/с): Q ~ 105; 3) камертон: Q ~ 104; 4) колебания кварцевой пластины: Q ~ 105; 5) излучение атома как колебательной системы: Q ~ 107. .
. )
) . (5.58)
. (5.58) ,
,  . (5.59)
. (5.59)


