Этап 3: объединение конечных элементов в ансамбльОснову этого этапа составляет замена произвольно назначенных выше номеров узлов i, j на номера, присвоенные узлам в процессе разбиения рассматриваемой области. Эта процедура приводит к системе линейных алгебраических уравнений, позволяющей при известных узловых значениях искомой функции получить значение последней в любой точке области. Рассмотрим процедуру составления ансамбля конечных элементов для задачи нахождения поля температур в стержне (рис. 2.18, а). Кусочно-элементная модель области приведена на рис. 2.18, б, а функция отдельного элемента определяется уравнением (2.50). Пример использования МКЭ для расчета одномерного температурного поля в однородном стержне длиной L и площадью поперечного сечения S (рис. 2.17). [1, 6]
Рис. 2.17. Однородный стержень, находящийся
Один конец стержня закреплен, к нему подводится тепловой поток q заданной интенсивности. На свободном конце стержня происходит конвективный теплообмен с внешней средой. Коэффициент теплообмена α, температура окружающей среды Т* известны. Вдоль боковой поверхности стержень теплоизолирован. Температурное поле в стержне описывается уравнением теплопроводности, которое в одномерном приближении имеет вид
Краевые условия определяются уравнениями:
Искомое температурное поле является непрерывной функцией координаты х (рис. 2.18, а).
Рис. 2.18. Расчет одномерного температурного поля
В МКЭ стержень разбивается произвольным образом на конечные элементы (в данном случае отрезки неравной длины). На каждом элементе непрерывная функция Т (х) аппроксимируется некоторой линейной зависимостью, как показано на рис. 2.18, б (в скобках указаны номера элементов). Аппроксимирующая кусочно-линейная функция определяется через узловые значения T1-Т6, которые в общем случае сначала неизвестны и подлежат определению в МКЭ. Запишем соответствие между произвольными номерами i, j, уравнения (2.50), и глобальными номерами узлов рассматриваемой дискретной модели для элемента 1: i = 1, j = 2, (2.58, а) элемента 2: i = 2, j = 3, (2.58, б) элемента 3: i = 3, j = 4, (2.58, в) элемента 4: i = 4, j = 5, (2.58, г) элемента 5: i = 5, j = 6. (2.58, д)
Подставив значения номеров узлов (2.58) в (2.50), получим:
где верхние индексы в скобках относятся к номеру элемента. В выражениях для функций формы элемента (2.49) значения произвольных номеров i, j также следует изменить в соответствии с (2.58). Тогда значения
Очевидно, что Рассмотрим пример объединения элементов двумерной области в ансамбль, который потребуется для иллюстрации дальнейших этапов МКЭ. Треугольная область разбита на элементы треугольной формы, как показано на рис. 2.19. Для обозначения узлов отдельных элементов по-прежнему используются номера i, j, k, начиная с произвольного узла (на рисунке отмеченного звездочкой) против часовой стрелки. Соответствие между этими обозначениями и глобальными номерами узлов следующее:
элемента 1: i = 1, j = 2, k = 4, (2.60, а) элемента 2: i = 1, j = 3, k = 5, (2.60, б) элемента 3: i = 2, j = 5, k = 4, (2.60, в) элемента 4: i = 4, j = 5, k = 6, (2.60, г)
Рис. 2.19. Пример составления ансамбля конечных элементов для двухмерной треугольной области
Подставляя значения (2.60) в (2.54), получим:
Аналогичную замену номеров необходимо проделать в (2.55) при вычислении функций формы элементов. Система (2.61) — сокращенная форма математического описания модели. Расширенная форма имеет вид:
или в матричной форме φ = NФ. (2.62) В САПР с целью уменьшения объема памяти чаще используют сокращенную форму описания моделей (2.61). Расширенная форма описания моделей имеет некоторые преимущества при реализации следующих этапов алгоритма МКЭ. Определение вектора узловых значений функций. Для этой цели используется несколько методов. Метод, основанный на вариационной постановке задачи, требует минимизации некоторого специально подобранного функционала, который связан с физическим смыслом задачи. Подбор функционала является нетривиальной процедурой, требующей глубоких знаний в конкретной предметной области. Пример минимизации функционала в задаче нахождении распределения температуры в однородном стержне (рис. 2.18). При указанном методе минимизируется функционал:
где V — объем тела; S — площадь границы. В функционал F входят оба граничных условия (2.57 а, б). При минимизации функционала используется множество функций элементов дискретизированной области. Для простоты вычислений будем считать, что стержень разбит всего на два элемента (в практических случаях этого недостаточно) (рис. 2.20).
Рис. 2.20. Пример минимизации функционала нахождения распределения температуры в стержне
Тогда
Функционал (2.63) удобно представить в виде
где S1 и S2 — площади сечений стержня, на которых заданы граничные условия (2.57 а) и (2.57 б) соответственно.
Для вычисления объемного интеграла в (2.65) его необходимо разбить на два слагаемых в соответствии с принятой конечной элементной моделью:
Производные в (2.66) вычисляются с учетом (2.64) и (2.49):
Подставив (2.67) в (2.66) и считая, что
Второе и третье слагаемые в (2.65) вычисляются просто так как подынтегральным функциям соответствуют узловые значения Т 1 и Т 3:
где S 1 и S 2 — площади поверхностей, на которых заданы q и α (для рассматриваемого примера
Значение функционала F вычисляется простым суммированием последних трех выражений:
где
Для минимизации функционала F необходимо выполнение условий:
или в матричной форме
В общем виде (2.69) можно представить так: Примечание. Матрица коэффициентов К в (2.69) по-прежнему называется матрицей жесткости, хотя по физическому смыслу данной задачи ее удобнее было бы назвать матрицей теплопроводности. Такое название матрицы К пришло из строительной механики, где МКЭ начал применяться раньше, чем в других областях техники. Зная характеристики материала, из системы (2.69) можно определить узловые значения T 1, Т 2, Т 3. Из (2.68) и (2.69) нетрудно заметить, что однотипные конечные элементы вносят в эти выражения слагаемые одного вида. Поэтому при реализации МКЭ в САПР вклад элемента определенного типа в матрицу жесткости вычисляется только один раз, а затем используется во всех необходимых случаях. При этом алгоритм получения матрицы жесткости несколько отличается от описанного выше и состоит из следующих этапов: Этап 1. Представление функционала F в виде суммы соответствующих функционалов для элементов. Для рассмотренного примера
Этап 2. Минимизация функционала каждого элемента отдельно (при этом вычисляются матрицы жесткости К (е) и векторы нагрузки В (е) для всех конечных элементов). В примере
Этап 3. Суммирование матриц жесткости и векторов нагрузки отдельных элементов [сумма приравнивается нулю, что позволяет получить систему КФ = В (2.45)]. Минимизация специально подобранного функционала при определении вектора узловых значений широко используется при анализе прочности конструкций. При этом если в качестве степеней свободы выбраны напряжения, то минимизируется функционал, описывающий дополнительную работу системы. Если же степенями свободы выбраны перемещения, то минимизируется и потенциальная энергия системы. Пример минимизации функционала в задаче о кручении стержня (рис. 2.21).
Рис. 2.21. Упругий стержень, находящийся под воздействием крутящего момента
Задача описывается уравнением
Для определения напряжений необходимо знать форму сечения стержня. В случае квадратного сечения стержня из-за наличия симметрии при решении задачи достаточно рассмотреть 1/8 его часть. Рассмотрение исследуемой части сечения стержня на элементы показано на рисунке 2.22.
Рис. 2.22. Поперечное сечение стержня, находящегося
На практике такое разбиение стержня слишком трудно, поэтому функционал F представим суммой функционалов, относящиеся к отдельным элементам сечения стержня:
Рассмотрим один из функционалов
и, введя обозначения
преобразуем выражение к виду
С учетом (2.62) вектор g(е) запишется в виде
или g(e) = D(e)Ф, где D(e) — матрица градиентов.
Подставив (2.71) в (2.70), получим
Минимизация функционала F (e) приводит к уравнению
где есть матрица жесткости, а
есть вектор нагрузки отдельного элемента. Вычисление по (2.72) и (2.73) проведем на примере первого элемента. С учетом первого уравнения системы (2.61) матрицу градиентов D(1) можно представить в виде
где
Произведение матриц
где
Все это выражение — постоянная величина, которая может быть вынесена из–под знака интеграла. С учетом сказанного и принимая для простоты толщину элемента равной 1, матрицу жесткости можно вычислить по формуле
Для определения вектора нагрузки (2.73) удобно воспользоваться интегральной формулой, позволяющей вычислять интегралы по площади двумерных симплекс–элементов:
В частном случае при а = 1, b = 0, с = 0 формула имеет вид
С учетом принятого допущения о единичной толщине элемента и формулы (2.75) вектор нагрузки В (1) для первого элемента запишется в виде
Аналогичные вычисления необходимо проделать и для всех остальных элементов области. Принимая, что площади всех элементов равны, а свойства материала одинаковы, и объединяя уравнения для элементов, получим полную систему уравнений:
При реализации МКЭ в САПР форма (2.74) матрицы жесткости элемента неэффективна с точки зрения затрат ОП. Действительно, матрицы жесткости отдельных элементов имеют ту же размерность, что и глобальная матрица жесткости системы, а большинство элементов матрицы нулевые. В САПР с целью сокращения затрат ОП из матриц жесткости исключают нулевые элементы, строя их в сокращенной форме. Такой метод построения матриц называют методом прямой жесткости. При этом исключается необходимость хранения матриц большой размерности, но возникает потребность в специальной процедуре кодирования узлов элементов. Суть этой процедуры заключается в том, что сначала вычисляются матрицы жесткости элементов в сокращенной форме. Например, в рассмотренном выше примере матрица жесткости К(1) будет иметь вид
Вектор нагрузки также вычисляется в сокращенном виде:
Затем строкам и столбцам матриц жесткости отдельных элементов приписываются глобальные номера элементов и тем самым определяется их место в общей матрице жесткости системы. Аналогично производится формирование глобального вектора нагрузки. Сочетание метода Галеркина с МКЭ приводит к системе уравнений [6]
где L(φ) — левая часть исходного дифференциального уравнения, описывающего непрерывную функцию φ. Технику получения разрешающей системы уравнений методом Галеркина легко проиллюстрировать на примере уже решенной выше задачи об отыскании температурного поля в однородном стержне (рис. 2.17), конечно–элементная модель которого представлена на рис. 2.21.
Применив метод Галеркина к (2.42), получим
Подставим в (2.76) формулу дифференцирования произведений:
Интерполяционная функция Т не сохраняет постоянства по длине стержня, поэтому интеграл в (2.77) можно представить суммой соответствующих интегралов для отдельных элементов. Так, второй интеграл в (2.77) можно представить в виде
Вычислим в этом уравнении интегралы, относящиеся к отдельным элементам:
С учетом (2.78) и (2.79)
Первый интеграл в (2.77) на основании теоремы Остроградского–Гаусса преобразуется к виду
где С учетом краевого условия (2.43 а) в точке для первого элемента интеграл (2.80) принимает вид
Подставив значения
С учетом краевого условия (2.43 б) в точке
Просуммировав выражения вида (2.80) для первого и второго элементов и выражения (2.82) и (2.83) и приравняв сумму нулю, получим систему уравнений
где
Система (2.84) идентична системе (2.68), определенной путем минимизации соответствующим образом подобранного функционала. Завершающим шагом этапа определения вектора силовых значений Ф является решение системы линейных алгебраических уравнений. Примечание. Основные особенности этого шага — большая размерность и сильная разреженность матрицы коэффициентов системы. В связи с этим для реализации МКЭ в САПР разработаны специальные способы хранения матрицы жесткости, позволяющие уменьшить необходимый для этого объем ОП. Для нахождения узловых значений функций применяются методы преобразования и решения системы, направленные на снижение затрат машинного времени. Нестационарные краевые задачи. Во всех рассмотренных выше примерах МКЭ применялся для решения стационарных краевых задач. Алгоритм метода и особенности отдельных его этапов остаются неизменными при решении нестационарных задач, в уравнениях которых присутствуют не только частные производные по пространственным координатам, но и частные производные по времени. В этом случае член с частной производной по времени рассматривается как функция пространственных координат в каждый фиксированный момент времени, или, как принято говорить, на каждом шаге численного интегрирования по времени. В рассмотренной выше задаче нестационарное температурное поле в стержне описывается уравнением
В этом случае при вариационной формулировке задачи минимизации подлежит функционал
Функционал (2.86) отличается от минимизированного выше функционала (2.62) наличием дополнительного слагаемого в объемном интеграле. Вычислим вклад этого слагаемого в результирующую систему уравнений. Для этого обозначим
Принимая, что характеристики материала постоянны по всему объему стержня, перепишем данное уравнение в виде
Интеграл F 1 можно представить суммой интегралов, записанных для отдельных элементов:
Используя соотношение T(e) = N(e)T(e) и учитывая, что N (e) является функцией только координат, производную по времени в (2.87) представим в виде
Тогда для отдельного элемента функционал F 1 записывается в форме
Продифференцировав (2.88) по вектору Т (е) и приравняв результат нулю, получим
Подставляя в объемный интеграл (2.89) соотношения для функций формы (2.50) и учитывая соотношение D(e) = S(e)dL(e), найдем
После суммирования по элементам и с учетом (2.90) функционал F 1 принимает вид
где H(1) = D(1)S(1)L(1)/ 6 и H(2) = D(2)S(2)L(2)/ 6.
Объединяя (2.91) с ранее полученным для той же задачи уравнением (2.68), результирующую систему уравнений для задачи (2.85) запишем в форме
2.5.3. Программные комплексы конечно–элементного
|


 . (2.56)
. (2.56) при х= 0; (2.57, а)
при х= 0; (2.57, а) при x = L. (2.57, б)
при x = L. (2.57, б)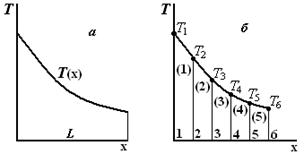
 (2.59)
(2.59) ,
,  определяются по формулам:
определяются по формулам:

 (2.61)
(2.61)
 , (2.63)
, (2.63)
 (2.64)
(2.64) , (2.65)
, (2.65) . (2.66)
. (2.66) (2.67)
(2.67) , получим
, получим .
. ;
; ,
, и
и  ).
). .(2.68)
.(2.68) и
и  .
.
 . (2.69)
. (2.69) , что соответствует (2.45).
, что соответствует (2.45).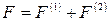 , причем
, причем ;
; .
.
 .
.
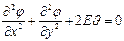 , отыскание напряжений в сечении связано с минимизацией дополнительной работы системы. В случае краевых условий первого рода φ = 0 соответствующий функционал имеет вид:
, отыскание напряжений в сечении связано с минимизацией дополнительной работы системы. В случае краевых условий первого рода φ = 0 соответствующий функционал имеет вид: .
.
 .
.
 ,
, . (2.70)
. (2.70) , (2.71)
, (2.71) .
. ,
, (2.72)
(2.72)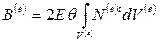 (2.73)
(2.73)

 равно
равно ,
, .
. . (2.74)
. (2.74) .
. . (2.75)
. (2.75) .
.

 .
. .
.
 . (2.76)
. (2.76) . (2.77)
. (2.77)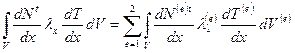 .
. ; (2.78)
; (2.78) . (2.79)
. (2.79)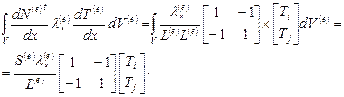 ….(2.80)
….(2.80)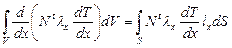 , (2.80)
, (2.80) ; n — внешняя нормаль к рассматриваемой поверхности.
; n — внешняя нормаль к рассматриваемой поверхности. . (2.81)
. (2.81) ,
,  в (2.81), получим
в (2.81), получим . (2.82)
. (2.82) второго элемента интеграл (2.82) запишется так:
второго элемента интеграл (2.82) запишется так: …………..(2.83)
…………..(2.83) , …...(2.84)
, …...(2.84) .
. . (2.85)
. (2.85) . (2.86)
. (2.86)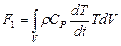 .
. .
. . (2.87)
. (2.87) .
. . (2.88)
. (2.88) . (2.89)
. (2.89) (2.90)
(2.90) (2.91)
(2.91) . (2.92)
. (2.92)


