Соединение узловЧрезвычайно популярный подход к проблеме построения сетки состоит в соединении узлов. Метод делится на две основные фазы: создание узлов и построение элементов. Создание узлов Можно выделить следующие методы создания узлов: § Метод Кавендиша. По этому методу работа начинается с задания граничных узлов вручную. Затем программа осуществляет создание внутренних узлов с учетом требований к плотности ячеек. Объект делится на участки, размер которых соответствует размеру элементов. В участке i создается квадратная сетка масштаба r(i). Одиночная сетка, построенная в предположении, что плотность конечной сетки должна быть постоянной, изображена на рис. В каждом квадрате сетки случайным образом создается один внутренний узел. Это может быть реализовано выбором двух случайных чисел от 0 до 1 и расчетом координат точки по соответствующим осям квадратной ячейки. Если узел попадает внутрь объекта, а расстояние от него до граничных и автоматически созданных на предыдущих шагах алгоритма узлов оказывается большим r(i), этот узел считается принятым. Иначе случайным образом выбирается следующий узел, который проходит ту же проверку. Если за фиксированное количество попыток (например, пять) принять узел не удается, квадратная ячейка сетки просто пропускается, и программа переходит к следующей ячейке. Этот метод может быть расширен до трех измерений простым переходом от плоской квадратной сетки к пространственной кубической.
Рис. 2.24. Создание узлов по методу Кавендиша
§ Метод Шимады. Этот метод требует представления внутренней области объекта заполненной пузырьками (рис.). Центральные точки пузырьков становятся узлами. Размер пузырька определяется температурным распределением, соответствующим заданной плотности сетки. Положения пузырьков определяются условиями равновесия с учетом всех сил реакции, действующих между ними.
Построение элементов На этом этапе осуществляется соединение узлов, в результате чего получаются элементы, которые не должны перекрываться, но должны покрывать всю площадь объекта. Будем учитывать только те элементы, у которых узлы находятся в вершинах. Если задача требует использования элементов с промежуточными узлами, их легко можно построить по элементам с узлами в вершинах. Основные методы построения элементов: § Метод Ли. Согласно этому методу на объект накладывается квадратная сетка, размер ячеек которой соответствует ожидаемому размеру элементов. Затем узлы, полученные на предыдущем этапе, связываются с ячейками этой сетки. Ячейки и соответствующие им узлы перебираются по столбцам слева направо и сверху вниз. Внутри ячейки узлы упорядочиваются по возрастанию абсцисс. Узлы с одинаковыми абсциссами сортируются по возрастанию ординат. Узлы перебираются последовательно, причем из соседних узлов выбираются такие, с которыми данный узел образует «хороший» четырехугольник. Если же четырехугольник оказывается «плохим», вместо него формируется треугольник. § Триангуляция Делоне. Наиболее популярный метод формирования треугольников путем соединения узлов, ориентированный на то, чтобы по возможности избегать формирования узких треугольников (максимизация суммы наименьших углов во всех треугольниках).
2.5.4. Сравнение методов конечных элементов и конечных Методы МКЭ и МКР относятся к классу сеточных методов приближенного решения краевых задач. С точки зрения теоретических оценок точности методы обладают примерно равными возможностями. В зависимости от формы области краевых условий, коэффициентов исходного уравнения оба метода имеют погрешности аппроксимации от первого до четвертого порядка относительно шага. В силу этого они успешно используются для разработки программных комплексов автоматизированного проектирования технических объектов. МКЭ и МКР имеют ряд существенных отличий: [5, 6] Прежде всего, они различны в том, что в МКР аппроксимируется производные искомых функций, а в МКЭ - само решение, т. е. зависимость искомых функций от пространственных координат и времени, Они сильно отличаются в способе построения сеток: в МКР строятся, как правило, регулярные сетки, особенности геометрии области учитываются только в околограничных узлах. В связи с этим МКР чаще применяется для анализа задач с прямолинейными границами областей определения функций. К числу традиционных задач, решаемых на основе МКР, относятся исследования течений жидкостей и газов в трубах, каналах с учетом теплообменных процессов и ряд других. В МКЭ разбиение на элементы производится с учетом геометрических особенностей области, процесс разбиения начинается от границы с целью наилучшей аппроксимации ее геометрии. Затем разбивают на элементы внутренние области, причем алгоритм разбиения строится так, чтобы элементы удовлетворяли некоторым ограничениям, например, стороны треугольников не слишком отличались по длине и т. д. Поэтому МКЭ наиболее часто используется для решения задач с произвольной областью определения функций, таких, как расчет на прочность деталей и узлов строительных конструкций, авиационных и космических аппаратов, теплой расчет двигателей и т. д. Общей проблемой методов является высокая размерность результирующей системы алгебраических уравнений (несколько десятков тысяч в реальных задачах). Поэтому реализация МКР и МКЭ в составе САПР требует разработки специальных способов хранения матрицы коэффициентов системы и методов решения последней.
2.6. Метод граничных элементов 2.6.1. Основные положения метода граничных элементов Когда инженер (ученый) строит количественную математическую модель системы любого рода, он обычно начинает с установления поведения бесконечно малого ее элемента на основании предполагаемых соотношений между главными переменными, характеризующими систему. Это приводит к описанию системы при помощи дифференциальных уравнений. Как только построена основная модель и выяснены свойства конкретного дифференциального уравнения, дальнейшие усилия направляются на получение решения уравнений в конкретной области, которая часто имеет очень сложную форму и состоит из различных сред, имеющих сложные свойства. На границах области задаются различные условия; они могут быть постоянными или меняться со временем и т.д. Поэтому решение таких дифференциальных уравнений было основным делом аналитиков в течение более двух столетий. Наличие нерегулярных границ в большинстве практических задач не позволяет построить аналитическое решение дифференциальных уравнений, и численные методы стали единственным возможным средством получения достаточно точных и подробных результатов. Наиболее широко используемые в настоящее время численные методы рассматривают дифференциальные уравнения непосредственно в той форме, в которой они были выведены, при помощи одного из двух подходов [6]: § при помощи аппроксимации дифференциальных операторов в уравнениях более простыми локализованными алгебраическими операторами, действующими в последовательностях узлов, находящихся в области; § при помощи представления самой области элементами среды, не являющимися бесконечно малыми (т.е. конечными элементами), которые в совокупности аппроксимируют реальную систему. Альтернативным подходом к системе дифференциальных уравнений была бы попытка аналитически проинтегрировать их каким-нибудь способом или перед переходом к какой-либо системе дискретизации, или перед введением какой–либо аппроксимации. Какой бы метод ни использовали, чтобы найти решение, пытаются проинтегрировать дифференциальные уравнения, но сущность методов граничных интегральных уравнений состоит в преобразовании дифференциальных уравнений в эквивалентную систему интегральных уравнений в качестве первого шага решения задачи. Такая операция (если она окажется успешной) дает систему уравнений, включающую только значения переменных на границах области. В свою очередь любая схема дискретизации будет приводить лишь к разбиениям поверхности, ограничивающим область. Поэтому в любой однородной области требуется дискретизировать только поверхность, а не всю область (отсюда название метода — МГЭ), так, что область становится одним большим сложным «элементом» в смысле метода конечных элементов. Вывод граничных интегральных уравнений и их решение могут оказаться более сложными математически, чем рассмотренные нами методы (МКР и МКЭ). Это верно лишь отчасти, несмотря на то, что методы граничных интегральных уравнений в прошлом развивались лишь математиками. Сейчас с практической точки зрения доступны методы граничных элементов, развитые на основе идей интегральных уравнений. Эти методы широко применимы без использования доказательств существования и единственности для каждого отдельного решения. В результате они становятся теперь чрезвычайно популярными и реализуются в алгоритмах для быстродействующих компьютерных систем.
2.6.2. Исторический обзор развития методов граничных В то время как главные свойства дифференциальных уравнений были хорошо уяснены в XIX веке, первое строгое исследование интегральных уравнений классических видов было опубликовано Фредгольмом только в 1905г. С тех пор они интенсивно изучались и существует много учебников, излагающих эти результаты. Значительный вклад в формальное понимание интегральных уравнений был сделан позднее С.Г. Михлиным. Несмотря на большие успехи, достигнутые в классификации и анализе свойств интегральных уравнений, оказалось, что никто из крупных авторов, не рассматривал возможности построения основанного на этих уравнениях общего численного алгоритма решения широкого класса практических задач. Толчок этому развитию был дан созданием быстродействующих ЭВМ, и результатом было появления метода граничных элементов. МГЭ был разработан в Саутгемптонском университете на основе проведенных там исследований по методам решения классических интегральных уравнений и конечным элементам. Мощным стимулом к развитию МГЭ послужило создание быстродействующих ЭВМ. Хотя все МГЭ имеют общее происхождение, они естественным образом делятся на три различные, но тесно связанные между собой категории. [6] Прямой вариант МГЭ. В этом варианте неизвестные функции, входящие в интегральные уравнения, являются реальными, имеющими физический смысл переменными задачи. В задачах теории упругости такое решение интегрального уравнения должно сразу давать все усилия и смещения на границе, возникающие в элементах конструкции, а внутри тела они должны быть получены из граничных значений численным интегрированием. Некоторые из разработанных алгоритмов, основанных на этом подходе описаны Крузом (Cruse T.A.), Лаша (Lachat J.C.), Риццо (Rizzo F.J.), Шоу (Shaw R.P.) Уотсоном (Watson J.O.) и другими и названы ими методами граничных интегральных уравнений. Полупрямые варианты МГЭ. В качестве альтернативы можно составлять интегральные уравнения для неизвестных функций, аналогичных функциям напряжений в теории упругости. Когда получено решение для этих функций, простое дифференцирование даст, например, распределение внутренних напряжений. Этот подход, известный под названием полупрямого метода, был развит Генри (Henry A.S.), Джесуоном (Jaswon M.A.), Понтером (Ponter A.R.), Римом (Rim K.) и Симмом (Simm G.T.). Непрямые варианты МГЭ. В непрямом варианте интегральные уравнения полностью выражаются через фундаментальное сингулярное решение исходных дифференциальных уравнений, распределенной с неизвестной плотностью по границам рассматриваемой области. Сами по себе функции плотности не имеют определенного физического смысла, но, когда они найдены (численным решением интегральных уравнений), значения параметров решения внутри тела могут быть получены из них простым интегрированием. Алгоритмы, основанные на таком подходе, описаны Бенерджи (Banerjee P.K.), Баттерфилдом (Butterfield R.), Хессом (Hess J.L.), Джесуоном (Jaswon M.A.), Массоне (Massonnet C.E.), и другими, использовавшими их для решения широкого круга технических задач. По мнению большинства ученых, занимавшихся исследованием МГЭ, прямые и непрямые варианты МГЭ в общем случае оказываются значительно полезнее полупрямого подхода; непрямой МГЭ особенно ясно и просто с физической точки зрения иллюстрирует основную процедуру решения. Все разновидности МГЭ используют принцип суперпозиции, поэтому область их применения ограничена классом полностью линейных или линейных относительно приращений задач. Однако к такому классу относятся многие важные для развития техники задачи, например МГЭ успешно используются для решения задач теории упругости, механики жидкости и газов. В любом варианте МГЭ результатом перехода от ДУЧП к интегральным уравнениям в конечном счете является система уравнений, включающая значения переменных только на границе заданной области. Поэтому в отличие МКЭ и МКР последующая дискретизация задачи проводится только на границе исследуемой области. Это обусловливает, во-первых, более высокую по сравнению с МКР и МКЭ точность решения, во-вторых, существенно меньший объем входных данных при реализации методов на ЭВМ. Область применения. В принципе эти методы могут быть применены к любой задаче, для которой дифференциальное уравнение или линейно, или линейно относительно приращений. В задачах, сводящихся к эллиптическим дифференциальным уравнениям, решения получаются сразу, в то время как для параболических и гиперболических систем уравнений должны быть введены процессы продвижения по времени. Таким образом, охватывается очень широкий класс физических задач; при помощи прямых или непрямых формулировок МГЭ могут быть решены, например, задачи об установившемся и неустановившемся потенциальных течениях, задачи статической и динамической теории упругости, упругопластичности, акустики и др. МГЭ может быть также использован в сочетании с другими численными методами, такими, как МКЭ или МКР, т.е. в смешанных формулировках. Соответствующие комбинированные решения почти неограниченно расширяют область применения методов, ибо МГЭ обладает четко выраженными преимуществами для областей больших размеров, в то время как методы конечных элементов являются удобным средством включения в такие системы объектов конечного размера или уточнения поведения решения в зонах быстрого изменения свойств.
2.6.3. Переход от исходного дифференциального уравнения При решении краевых задач приближенные модели технических объектов можно строить на основе интегральных уравнений. При этом первый шаг на пути к решению состоит в переходе от дифференциальных уравнений в частных производных к эквивалентным интегральным уравнениям. Во многих случаях, когда такой переход оказывается успешным, решение исходной задачи может быть получено с минимальными вычислительными затратами и высокой степенью точности. Кроме того, размерность исходной задачи понижается на единицу, двухмерные задачи преобразуются в одномерные. Рассмотрим на простом примере алгоритм перехода. В двумерной однородной области произвольной формы с коэффициентом проницаемости k требуется найти распределение функции φ, описанной уравнением
которое является частным случаем квазигармонического уравнения
На границе L рассматриваемой области заданны граничные условия первого рода
φ (x0) = g(x0). (2.94) Этап 1. Нахождение сингулярного решения. В МГЭ используется то обстоятельство, что для большинства уравнений в частных производных существуют сингулярные (фундаментальные) решения, отвечающие единичным возмущающим воздействиям в неограниченной области. Для рассматриваемой задачи сингулярное решение записывается в виде
φ (x) = G(x, ξ) g(ξ), (2.95) где φ (x) — значение искомой функции в произвольной точке области; g(ξ) — единичное возмущающее воздействие, приложенное в точке ξ. Начала координат для систем х и ξ совпадают. Величина G(x, ξ) определяется, в свою очередь уравнением
где Этап 2. Введение фиктивных источников. Рассматриваемая область G1 «помещается» в бесконечную область, для которой известно решение (2.95). Потребуем, чтобы значения φ (x) на границе области совпадали с заданным граничным условием (2.94). Чтобы это требование выполнялось, введем на границе фиктивные источники неизвестной интенсивности p(ξ) в расчете на единицу длины границы L. Подставив p(ξ) в (2.95) и проинтегрировав его по длине границы, получим; искомое решение:
В результате проделанных действий от исходного дифференциального уравнения (2.93) удалось перейти эквивалентному интегральному уравнению (2.96), в котором появилась произвольная постоянная С, обеспечивающая единственное решение в связи с тем, что функция φ (x) рассчитывается относительно некоторого нулевого значения. В дальнейшем С подбирается таким образом, чтобы суммарное «излучение» от всех источников обращалось в нуль на бесконечно удаленной границе. Для обеспечения заданных граничных условий необходимо, чтобы выполнялось равенство
На основании равенства (2.97) строится система интегральных уравнений относительно неизвестных фиктивных источников p(ξ). После того как они будут найдены, значения искомой функции φ (x) в любой внутренней точке области легко определяются из (2.96). Если бы (2.97) удалось проинтегрировать аналитически, то для исходной задачи было бы найдено точное решение. На практике (2.97) решается приближенно, что является единственным источником погрешности в МГЭ. 2.6.4. Дискретизация границы рассматриваемой области Для приближенного решения (2.97) производится дискретизация границы рассматриваемой области. Аналогично МКЭ разбиение границы на элементы можно производить различными способами. В простейшем случае граница аппроксимируется линейными элементами. Отдельный элемент определяется координатой своей средней точки. Интенсивность неизвестных источников p(ξ) в пределах элемента принимается постоянной. С учетом принятых допущений выражение (2.97) запишется в виде
где
Уравнение (2.98) определяет значение функции в средней точке q –го граничного элемента. В матричной форме (2.98) принимает вид
где Δ L — длина q -го граничного элемента; р(е) — вектор-столбец размерности N;
При этом каждый элемент вектора-строки определяется по формуле
С учетом (2.100) уравнение (2.99) перепишется так:
φ q = Gqep(e) + C.
Составляя аналогичные уравнения для каждого граничного элемента и проводя суммирование по всем элементам, получим систему алгебраических уравнений
φ = GSp(e) + IC, где φ и р — N –мерные векторы; I — единичный N –мерный вектор–столбец; GS — матрица коэффициентов размерности NхN.
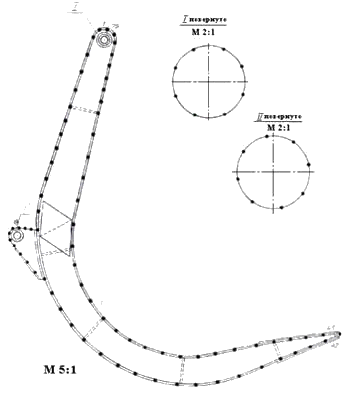
2.6.5. Алгоритм метода граничных элементов При реализации на ЭВМ алгоритм МГЭ состоит из следующих этапов [4]: Этап 1. Формирование входных данных. Данный этап, который является первым шагом выполнения любой инженерной программы, основан на концепции макроэлементов, позволяющей значительно сократить и упростить процедуру ввода чисел. Применительно к плоской задаче теории упругости она состоит в том, что вся граница исследуемой упругой области разбивается на простые линии, выбираемые из библиотеки макроэлементов. Такими линиями могут быть отрезок прямой, часть параболы, дуга окружности или целая окружность. Следовательно, минимальная вводимая информация должна содержать количество и тип макроэлементов, число разбиений каждого макроэлемента на граничные элементы, тип граничных условий, координаты узлов макроэлементов и значения граничных перемещений и усилий в узлах макроэлементов. Этап 2. Интегрирование функций G (x, ξ) для получения матрицы коэффициентов GS. Этап 3. Составление разрешающей системы алгебраических уравнений. Отметим две важные особенности СЛАУ МГЭ. Во–первых, матрица является полностью заполненной и несимметричной. В этом состоит ее существенный недостаток и отличие от глобальной матрицы жесткости МКЭ, которая является разрешенной (т.е. с большим количеством нулевых элементов) и симметричной, что позволяет использовать более эффективные численные методы решения СЛАУ. Вторая особенность матрицы А состоит в том, что ее размер значительно меньше размера матрицы жесткости МКЭ, что существенно компенсирует отмеченные недостатки. Данная черта матрицы А объясняется тем, что в МГЭ неизвестными являются перемещения и усилия в узлах границы Г, в то время как МКЭ требует разбиения всей области Ω на конечные элементы. Следовательно, вектор неизвестных, определяющий размер матрицы СЛАУ, содержит значения перемещений (или сил) во всех узлах области Ω, число которых много больше граничных узлов. Этап 4. Решение системы для определения неизвестных фиктивных источников. Этап 5. Подстановка найденных значений в определяющее интегральное уравнение и вычисление значений функций во внутренних точках области. Этап 6. Вывод результатов. Выходная информация содержит основные сведения о гранично–элементной модели задачи (число макроэлементов, число граничных элементов, число узлов, число степеней свободы дискретной системы), тип плоского состояния (плоское напряженное или плоское деформированное), характеристики глобальной системы линейных алгебраических уравнений, результаты расчета (глобальные номера узлов и граничных элементов, значения перемещений, усилий и напряжений в узлах гранично–элементной сетки). Многие этапы рассмотренного алгоритма аналогичны соответствующим этапам МКЭ. Достаточно нетривиальным является этап 2 алгоритма, связанный с интегрированием функции G(x, ξ). Поэтому в целом программирование МГЭ требует несколько больших усилий по сравнению с реализацией МКЭ. Однако последующая эксплуатация программы проще с точки зрения пользователя, так как объем задаваемой входной информации значительно меньше, чем в МКЭ. Рассмотрим анализ напряженно-деформированного состояния детали механической конструкции — челюсти грейфера-захвата для древесины, выпускаемого компанией КРАНЕКС (г. Иваново). Требуется исследовать напряженно-деформированное состояние челюсти грейфера-захвата для древесины (рис. 2.25), определить опасные сечения, зоны концентрации напряжений, максимальные напряжения. Действующая нагрузка - вес поднимаемого груза, распределенного равномерно по небольшой площадке челюсти грейфер, равный 10 Н/мм. Рассматривается задача в статической линейной постановке в предположении реализации в исследуемой детали плоско-напряженного состояния. Для решения возникающей двумерной задачи теории упругости применен метод граничных элементов, реализованный в виде программы BPS, входящего в программный комплекс MechanicsFE.
Рис. 2.25. Конструкция грейфера
Первоначально разрабатывается так называемая макроэлементная модель конструкции, для чего определяются координаты характерных точек на поверхности, описывающих геометрию упругой области в целом. Число макроэлементов выбирается минимально возможным для наиболее точного описания границы тела. Затем с помощью специальной программы, называемой автоматическим генератором сетки, макроэлементы разбиваются на более мелкие граничные элементы. Тем самым формируется окончательная компьютерная модель конструкции (рис.2.26).
Рис. 2.26. Гранично-элементная модель челюсти захвата
На рис. 2.27 представлены результаты расчета задачи на выбранной сетки. Рисунок деформированной конструкции соответствует тому, что подсказывает здравый смысл — основная несущая часть челюсти грейфера изгибается под действием веса полезного груза. Наибольшие напряжения на внутренней границе тела возникают в зоне перехода от горизонтального участка челюсти к вертикальному, что соответствует теории изгиба консольного стержня. Однако максимальные напряжения локализуются в небольшой области вблизи выносной детали челюсти, предназначенной для шарнирного крепления подъемной тяги. Это говорит о концентрации напряжений в указанной зоне и, хотя предел прочности для данного вида стали не превышен при рассмотренной нагрузке на одну челюсть, требуется повышенное внимание к данному элементу конструкции в процессе эксплуатации (более частые профилактические осмотры, специальные методы диагностики, особенно на зарождение и распространение трещин). Необходимо дальнейшее исследование математической модели конструкции с целью оптимизации формы соединения деталей челюсти и минимизации возникающих напряжений.
Рис. 2.27. Деформированное состояние конструкции
Рис. 2.28. Распределение напряжений по внешней стороне
2.6.6. Сравнение особенностей МКЭ и МГЭ Применимость Все методы граничных интегральных уравнений используют принцип суперпозиции и поэтому применимы или к полностью линейным системам, или к тем, которые линейны относительно приращений либо могут быть аппроксимированы таковыми. Таким образом, последняя категория расширяет область применимости методов на очень многие интересные для технических наук задачи. Представляется, что существует очень мало задач, поддающихся решению при помощи методов конечных элементов, которые нельзя было бы по меньшей мере столь же эффективно решить при помощи МГЭ. Размерность задачи МГЭ уменьшает размерность исходной задачи на единицу, т.е. для двумерных задач получается одномерное граничное интегральное уравнение, а для трехмерных задач — всего лишь двумерные интегральные уравнения по поверхности. Из предпринятых различными авторами исследований (Лаша, Бенерджи) можно заключить, что сопоставляемые времена решения трехмерных задач методом конечных элементов и методом граничных элементов при близкой точности обычно оказываются в 4–10 раз меньше для последнего метода. Непрерывное моделирование полей внутри области МГЭ включает моделирование только граничной геометрии системы. Как только получена необходимая информация о границе, могут быть вычислены значения переменных, описывающих решение, в любых последовательно выбираемых внутренних точках. Более того, решение полностью непрерывно всюду внутри тела. Оказывается, что обе эти особенности присущи только МГЭ и выделяют его среди возможных альтернатив. В силу непрерывности решения исследователь может найти значения переменных в любой заданной внутренней точке, о выборе которой он может позаботиться после основного анализа, причем с очень высокой точностью, например, в областях концентрации напряжений в упругих телах. Точность и распределение погрешности Само по себе граничное интегральное уравнение является формулировкой поставленной задачи, ведущей к точному ее решению, и погрешности вследствие дискретизации и численной аппроксимации возникают только на границах и рядом с ними из-за невозможности выполнить численное интегрирование в замкнутой форме. Если процедура численного интегрирования сделана достаточно сложной (при использовании, например, криволинейных граничных элементов и непрерывно изменяющихся распределений функций на границе), то привносимые таким образом погрешности могут быть действительно очень малыми. Конечно же, численное интегрирование всегда представляет собой более устойчивый и точный процесс, чем численное интегрирование, и ни прямой, ни непрямой МГЭ не требуют дифференцирования численных величин. Вполне ясно, что при отсутствии объемных сил исследователь должен задать только информацию о геометрии границ области (в дополнение к граничным условиям и прочим данным, общим для всех методов решения). Таким образом, усилия, направленные на подготовку данных, существенно меньше, чем требуется для любого метода, включающего геометрическое моделирование внутренней части тела. Поэтому для подавляющего большинства практических задач МГЭ обладает очень существенными преимуществами по сравнению с методами конечных элементов.
|


 , (2.93)
, (2.93) при x1 = x, x2 = y.
при x1 = x, x2 = y.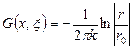 ,
,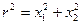 и r0 выбрано так, что G = 0 при r = r0. Уравнение (2.95) определяет искомую функцию φ (x) относительно некоторого нулевого значения при r = r0.
и r0 выбрано так, что G = 0 при r = r0. Уравнение (2.95) определяет искомую функцию φ (x) относительно некоторого нулевого значения при r = r0. . (2.96)
. (2.96)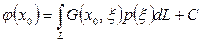 . (2.97)
. (2.97) (2.98)
(2.98) — координата средней точки q –го граничного элемента.
— координата средней точки q –го граничного элемента. , (2.99)
, (2.99) — вектор-строка той же размерности.
— вектор-строка той же размерности. . (2.100)
. (2.100)