Этап 1: выделение конечных элементов

Этап 1: выделение конечных элементов.

Разбиение области на элементы - важный этап в МКЭ. От качества разбиения во многом зависит точность получаемых результатов. Например, разбиение на двухмерные элементы, близкие по форме к равносторонним треугольникам, обеспечивает лучшие результаты по сравнению с разбиением на вытянутые по форме треугольные элементы. Возможность легко варьировать размерами элементов - важное свойство МКЭ (последнее позволяет без труда учитывать концентрацию напряжений, температурные градиенты, различные свойства материала изучаемого объекта и т. д.).

Разбиение области на элементы обычно начинают от ее границы с целью наиболее точной аппроксимации формы границы, затем производится разбиение внутренних областей. Часто разбиение области на элементы производят в несколько этапов. Сначала область разбивают на достаточно крупные подобласти (подконструкции), границы между которыми проходят там, где изменяются свойства материала, геометрия, приложенная нагрузка и пр. Затем каждая подобласть взбивается на элементы. Резкого изменения размеров конечных элементов на границах подобластей стараются избегать. На рис. 2.9. приведен пример разбиения двухмерной области произвольной формы на треугольные конечные элементы с криволинейными границами.

Нумерация узлов элементов (глобальная нумерация узлов) — следующая процедура этапа выделения конечных элементов. Порядок нумерации имеет в данном случае существенное значение, так как влияет на эффективность последующих вычислений.

 

Рис. 2.9. Разбиение двухмерной области произвольной формы на треугольные конечные элементы с криволинейными границами

 

Матрица коэффициентов системы линейных алгебраических уравнений, к которой приводит МКЭ, - сильно разреженная матрица ленточной структуры. Ненулевые элементы такой матрицы располагаются параллельно главной диагонали (рис. 2.10).

Рис. 2.10. Матрица ленточной структуры

 

Целое число L, представляющее собой наибольшую разность между номерами ненулевых элементов в строке, называется шириной полосы. Чем меньше ширина полосы, тем меньший объем ОП требуется для хранения матрицы при реализации МКЭ в САПР и тем меньше затраты машинного времени на решение результирующей системы уравнений. Ширина полосы зависит, в свою очередь, от числа степеней свободы узлов и способа нумерации последних.

Под числом степеней свободы понимают количество неизвестных функций, определяемых в каждом узле. Так, например, для двухмерных задач гидравлики в каждом узле определяют три переменные: давление и составляющие скорости по осям X и Y.

При нумерации узлов предпочтителен способ, обеспечивающий минимальную разность между номерами узлов в каждом отдельном элементе. Если максимальную разность между номерами узлов для отдельного элемента обозначить N, а число степеней свободы — М, то ширина полосы

 

L = (N + 1)M. (2.45)

 

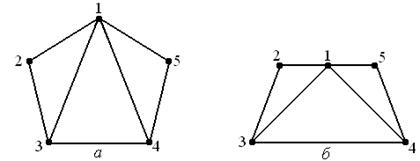
В некоторых случаях уменьшение числа N может быть достигнуто последовательной нумерацией узлов при движении в направлении наименьшего размера рассматриваемой области.

На рис. 2.11 приведены два различных способа нумерации узлов произвольной области, разбитой на конечные элементы. При первом способе (рис. 2.11, а) N = 14, при втором (рис. 2.11, б) N = 5. Ширина полосы для представленных способов при одной степени свободы в узле получается равной соответственно 15 и 6; при двух степенях свободы — 30 и 12. Рациональная нумерация в случае рис. 2.11, б сокращает необходимый объем ОП почти в три раза по сравнению со случаем рис. 2.11, а.

Рис. 2.11. Способы нумерации узлов при разбиении двухмерной области на конечные элементы

Информация о способе разбиения области наконечные элементы и нумерации узлов является исходной для всех следующих этапов алгоритмов МКЭ при реализации метода в САПР. При этом требуется указывать не только номер, но и координаты каждого узла и его принадлежность к определенным конечным элементам. Такого рода информация называется топологической и обычно содержит примерно в 6 раз больше чисел, чем количество узлов системы.

При описании области, разбитой на конечные элементы, необходимо задавать: тип конечного элемента; его порядковый номер; номера узлов элемента; координаты узлов, информацию о соединении элементов между собой; значение физических параметров объекта в пределах каждого конечного элемента. Промышленная эксплуатация программной системы долгое время тормозилась именно сложностью подготовки исходных данных, объем которых в некоторых случаях достигал нескольких сотен тысяч.

При решении задач проектирования летательного аппарата методом конечных элементов область определения искомой функции разбивается на несколько тысяч элементов примерно с таким же количеством узлов. В связи с этим возникают проблемы, связанные со сложностью подготовки столь большого количества исходной информации и с трудностью ее проверки и корректировки, так как при ручной подготовке такого объема исходных данных неизбежно появление ошибок.

Поэтому усилия разработчиков программ МКЭ в составе САПР в последние годы были направлены на создание подсистем автоматизированной подготовки топологической информации, основу которых составляют специальные программы, называемые препроцессорами.

Препроцессоры либо непосредственно включаются в состав программных комплексов, реализующих МК; либо существуют в виде автономных программ.

Алгоритм работы препроцессора, как правило, состоит из следующих этапов:

Этап 1. Нанесение на заданную область некоторого множества узлов.

Этап 2. Формирование узловых связей с целью заполнения области конечными элементами «наилучшей» формы.

Этап 3. Нумерация узлов, минимизирующая ширину полосы в матрице коэффициентов системы уравнений.

Последняя процедура поддается алгоритмизации особенно просто и реализована практически во всех крупных программных комплексах на основе МКЭ.

 

Алгоритмы формирования межузловых связей строятся на основе различных подходов. При этом в первую очередь стараются, если это возможно, использовать упрощающие предположения. Регулярность области удобно использовать для построения однородной сетки, шаг которой меняется по несложному закону. Криволинейные границы области часто аппроксимируют с помощью отрезков прямой, параболы или дуги.

В основу разбиения области произвольной формы на треугольные конечные элементы может быть положен следующий алгоритм:

Этап 1. Аппроксимация границы области совокупностью отрезков, представляемых номерами узлов.

Этап 2. Выбор вершин треугольников, основаниями которых служат полученные на этапе 1 отрезки (при этом выбор вершин разрешен только с одной вполне определенной стороны).

Этап 3. Соединение основания с выбранной вершиной отрезками, которые на следующем шаге сами будут рассматриваться как основания новых треугольников.

Алгоритм повторяется до тех пор, пока остается возможным строить новые элементы на базе проведенных отрезков, т. е. до полного заполнения области элементами.

Пример такого «послойного» заполнения области элементами приведен на рис. 2.12.

При построении очередного треугольника для анализа выбираются вначале два ближайших к основанию узла с «разрешенной» стороны. На выбранных узлах строится прямоугольник. Далее проводится топологический анализ, использующий информацию об уже построенных элементах. Целью анализа является исключение возможности попадания какого-либо узла внутрь построенного треугольника. На основании анализа выбирается одна из двух возможных вершин и четырехугольник делится на треугольники одним из двух возможных способов.

 

Рис 2.12. Пример использования алгоритма автоматического разбиения произвольной области на треугольные конечные элементы

 

Примером другого подхода к автоматическому разбиению области на элементы служит следующий алгоритм:

§ Определение граничных узлов области.

§ Построение регулярной сетки с тем же числом узлов, что и в заданной области.

§ Использование полученной схемы соединения узлов для области произвольной формы.

На рис. 2.13 приведен пример разбиения на треугольные конечные элементы области с пятью граничными узлами.

Рис. 2.13. Пример автоматического разбиения области с пятью граничными узлами на треугольные элементы: а — регулярная сетка; б — сетка в заданной области

 

Для построения регулярной сетки используется следующий алгоритм:

§ Окружение исходной точки кольцом равносторонних треугольников так, чтобы число внешних узлов было предельно близким к заданному числу граничных узлов.

§ Если желаемый результат не достигнут, то добавим еще один ряд колец.

На рис. 2.14. проиллюстрировано использование приведенного алгоритма для построения регулярной сетки «наилучшего» вида для границы с девятью узлами.

Рис. 2.14. Пример использования алгоритма автоматического построения сетки наилучшего вида в области с девятью граничными узлами

 

Полученная в результате проведенного построения схема соединения узлов позволяет получить координаты всех внутренних точек области. Если в результате выполнения алгоритма вид конечных элементов оказывается неудовлетво-рительным, то исходная область разбивается на подобласти и все повторяется сначала.