Частотный спектр периодического сигнала
Периодический сигнал S(t) изменяется непрерывно и имеет период Т0 повторения значений (рисунок 3.2). Такой сигнал может быть представлен бесконечной суммой гармонических колебаний:
Рисунок 3.2 - Периодический сигнал
В выражении (3.1) а0 представляет собой постоянную составляющую сигнала, принимающую среднее значение сигнала за период. Это может быть постоянный ток или постоянное напряжение. Затем следуют две составляющие
Эту частоту называют основной. Две следующих составляющих имеют частоту, равную удвоенной основной частоте, их называют вторыми гармониками. В общем случае ряд повторяется до бесконечности и частоты составляющих сигнала будут отличаться от основной частоты во все большее число раз, то есть появятся третья, четвертая и другие гармоники. Приведенный ряд (3.1) можно представить в компактном виде:
где k – номер гармонической составляющей, аk, bk – амплитуды k –гармоники. Такое разложение периодической функции времени называется рядом Фурье. Амплитуды и начальные фазы любой гармоники определяются следующими выражении:
Если ввести такие характеристики как общую амплитуду и начальную фазу k – гармоник, то ряд Фурье можно записать в виде:
Не все физические величины можно оценить одним числом. Например, напряжение на участках цепи переменного тока одной частоты могут отличаться по амплитуде и по фазе, т.е. для характеристики каждого из них необходимо как минимум два числа a и b. Для этого используется комплексное представление сигнала. Представим ряд Фурье в комплексной форме, заменяя тригонометрические функции показательными. Для замены тригонометрических функций показательными используются формулы Эйлера:
и обратные формулы Эйлера:
Подставив (3.6) в (3.3) и с учетом 1/j = –j, получим:
Обозначим:
Тогда с учетом (3.4) и (3.7) составляющие амплитуды примут вид:
Аналогично:
В этом выражении присутствует среднее значение функции S(t) или постоянная составляющая сигнала
Объединив обе суммы в выражении (3.11), получим комплексную форму записи ряда Фурье:
где Сk –комплексные амплитуды гармоник:
Таким образом ряд Фурье показывает, что периодическая функция времени S(t) может быть представлена не только своими мгновенными значениями, но также и своими гармоническими составляющими c частотами, кратными основной частоте. Пример представления периодического сигнала спектральными гармоническими составляющими представлен на рисунке 3.3:
Рисунок 3.3 – Частотный спектр периодического сигнала
|

 (3.1)
(3.1)
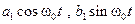 с частотой:
с частотой: . (3.2)
. (3.2)
 , (3.3)
, (3.3) ,
,  ; (3.4)
; (3.4) , где
, где ,
, . (3.5)
. (3.5) ;
; 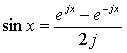 , (3.6)
, (3.6) ;
; 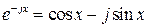 . (3.7)
. (3.7) (3.8)
(3.8)
 . (3.9)
. (3.9)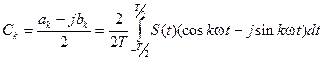
 . (3.10)
. (3.10) . Заметим, что выражение для Ck отличается от C-k: лишь знаком перед мнимой частью. Вводя отрицательные значения k, с учетом (3.10) ряд Фурье (3.8) примет вид:
. Заметим, что выражение для Ck отличается от C-k: лишь знаком перед мнимой частью. Вводя отрицательные значения k, с учетом (3.10) ряд Фурье (3.8) примет вид: (3.11)
(3.11) . Используя выражение (3.4) для составляющих амплитуды, будем иметь:
. Используя выражение (3.4) для составляющих амплитуды, будем иметь: .
. , (3.12)
, (3.12) (3.13)
(3.13)

 – огибающая модуля спектра последовательности прямоугольных импульсов.
– огибающая модуля спектра последовательности прямоугольных импульсов.



