Векторная алгебра.БИЛЕТ. 1 ВОПРОС. Числовой матрицей размера m
2 ВОПРОС. Правила линейных операций: 1.Пусть ПРИМЕР. 2. Произведением матрицы
ПРИМЕР. 3. Нулевой матрицей 4. Матрица
5. Разностью матриц 6. Результат конечного числа линейных операций над матрицами называется их линейной комбинацией. ПРИМЕР. Пусть Матрица комбинация матриц Транспонированной матрицей То есть, если
ПРИМЕР.
3х2 2х3 3х3 3х3 Пусть
то есть элемент
ПРИМЕР.
2х3 3х1 2х3 3х1 2х1 Произведение 3х1 2х3 БИЛЕТ. 1 ВОПРОС.
ПРИМЕР.
2 ВОПРОС. Матрицы
Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.
ПРИМЕР.
значит,
Вообще единичная матрица перестановочна с любой квадратной матрицей того же порядка, и для любой матрицы Если соответствующие произведения определены, то: 2. 3. 4. 5.
ПРИМЕР.
2х2 2х1 2х1 1х2
1х2 2х2 1х2
ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
ПРИМЕР. БИЛЕТ. Рассмотрим квадратную матрицу второго порядка: Её определителем называется число, которое записывается и вычисляется так:
Такой определитель называется определителем второго порядка и может обозначаться по-другому: Определителем третьего порядка называется число, соответствующее квадратной матрице
Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:
ПРИМЕР.
Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:
Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных. Из суммы первых трех произведений вычитается сумма остальных. Группируя слагаемые в (1.2) и используя (1.1), заметим, что
То есть при вычислении определителя третьего порядка используются определители второго порядка, причем БИЛЕТ. - БИЛЕТ. 1.ВОПРОС. Рангом матрицы А называется такое целое число 2 ВОПРОС. Ранг матрицы равен нулю тогда и только тогда, когда ее миноры равны нулю, то есть если матрица нулевая.
ПРИМЕР.
Матрица
БИЛЕТ. 1 ВОПРОС. Элементарными преобразованиями матрицы называются следующие действия: 1) умножение любой строки на число 2) перемена местами двух строк; 3) прибавление ко всем элементам строки соответствующих элементов другой строки, умноженных на одно и то же число 4) отбрасывание нулевой строки; 5) отбрасывание одной из двух пропорциональных строк; 6) те же преобразования со столбцами.
2 ВОПРОС. ТЕОРЕМА. Элементарные преобразования не изменяют ранга матрицы. С их помощью всякую матрицу можно привести к диагональному виду, и ее ранг равен количеству ненулевых элементов на главной диагонали (без доказательства). Покажем теперь, что ранг матрицы F из последнего примера равен 2.
При переходе от Вычислить
БИЛЕТ. 1 вопрос. Матрица Из определения следует, что 2 ВОПРОС –
БИЛЕТ. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений у нее более одного. ПРИМЕР.
БИЛЕТ. ТЕОРЕМА. (Кронекера-Капелли, критерий совместности системы линейных уравнений) Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной (без доказательства). СЛЕДСТВИЕ. Для того чтобы однородная система ДОКАЗАТЕЛЬСТВО. 1) Достаточность: Так как единственный минор 2) Необходимость: система имеет нетривиальное решение Если БИЛЕТ. 1 ВОПРОС. ТЕОРЕМА. Для того чтобы система линейных однородных уравнений (1.15) имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы ДОКАЗАТЕЛЬСТВО. 1) Достаточность: По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные. 2) Необходимость: (1.15) имеет нетривиальное решение Пусть ИЛИ СЛЕДСТВИЕ. Для того чтобы однородная система ДОКАЗАТЕЛЬСТВО. 1) Достаточность: Так как единственный минор 2) Необходимость: система имеет нетривиальное решение Если
БИЛЕТ. ПРИМЕР. Решить систему уравнений матричным способом:
В предыдущем примере было показано, что
Таким образом,
Вернемся к равенству (1.12). Из него следует, что
поэтому где
ПРИМЕР. Решить систему линейных уравнений: Выпишем расширенную матрицу и системы и упростим ее с помощью элементарных преобразований над строками:
Очевидно, что Кронекера-Капелли система совместна.
Выпишем систему, соответствующую матрице
Перенесем в правую часть переменные
Теперь подставим
Векторная алгебра. Билет. Вектором называется упорядоченная пара точек. Билет. Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления. Векторы Так как направление нулевого вектора не определено, то он коллинеарен любому другому. Векторы называются компланарными, если они параллельны одной плоскости. Нулевой вектор компланарен любой системе компланарных векторов.
|

 n называется совокупность
n называется совокупность  чисел, расположенных в виде таблицы, содержащей m строк и n столбцов.
чисел, расположенных в виде таблицы, содержащей m строк и n столбцов.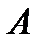 =
= 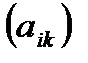 и
и 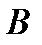 =
= 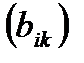 ,
, 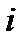 =1,2,…,
=1,2,…, 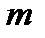 ,
, 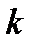 =1,2,…,
=1,2,…, 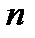 – матрицы размера
– матрицы размера  . Матрица
. Матрица  =
= 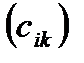 также размера
также размера 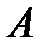 и
и 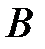 , если
, если 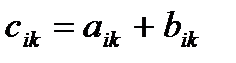 ,
, 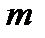 ,
,  =1,2,…,
=1,2,…, 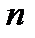
 =
= 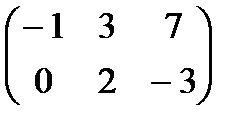 ,
,  =
= 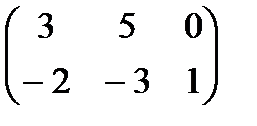
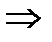
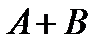 =
= 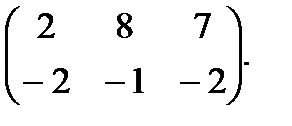
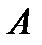 =
= 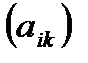 размера
размера  называется матрица
называется матрица 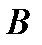 =
= 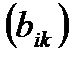 того же размера, элементы которой
того же размера, элементы которой 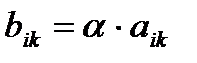 ,
, 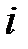 =1,2,…,
=1,2,…, 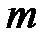 , k=1,2,…,
, k=1,2,…, 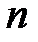 .
.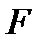 =
= 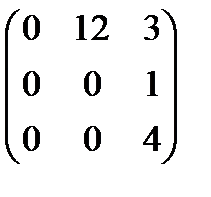
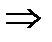
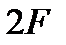 =
= 
 называется матрица, все элементы которой равны нулю.
называется матрица, все элементы которой равны нулю.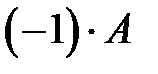 называется противоположной для
называется противоположной для 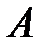 и обозначается
и обозначается 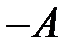 . Очевидно, что
. Очевидно, что 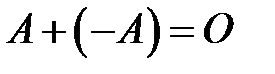 для любой матрицы А.
для любой матрицы А.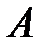 и
и 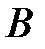 одного размера называется сумма
одного размера называется сумма 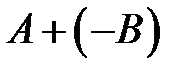 и обозначается
и обозначается 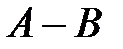 .
.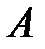 =
= 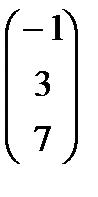 ,
, 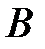 =
= 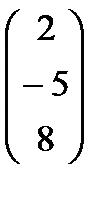 .
.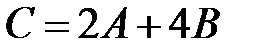 =
= 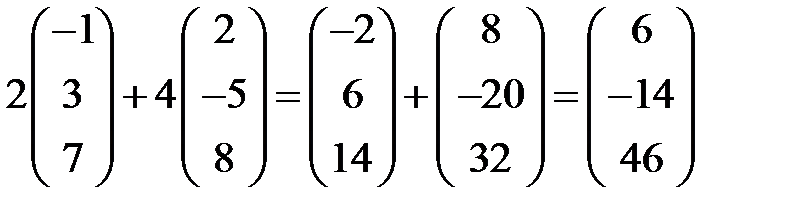 – линейная
– линейная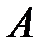 и
и 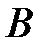 с коэффициентами 2 и 4.
с коэффициентами 2 и 4.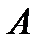
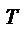 для матрицы
для матрицы 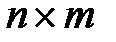 , полученная из
, полученная из 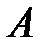 заменой всех ее строк столбцами с теми же порядковыми номерами.
заменой всех ее строк столбцами с теми же порядковыми номерами.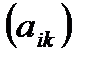 , то
, то 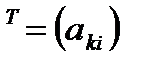 ,
, 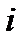 =1,2,…,
=1,2,…, 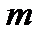 ,
, 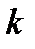 =1,2,…,
=1,2,…, 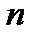 .
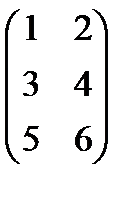
.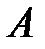 =
= 
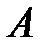
 ;
; 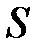 =
= 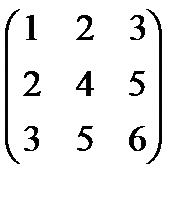 =
= 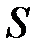
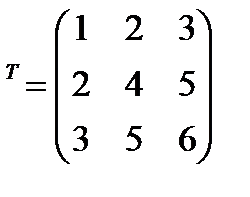
 =
=  – матрица размера
– матрица размера 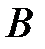 =
= 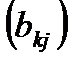 – матрица размера
– матрица размера 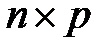 . Произведение этих матриц
. Произведение этих матриц 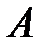
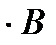 – матрица
– матрица  =
= 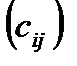 размера
размера 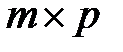 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле: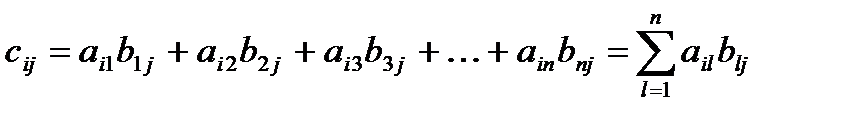 ,
, 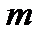 ,
, 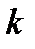 =1,2,…,
=1,2,…, 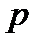 ,
,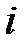 -й строки и
-й строки и  -го столбца матрицы
-го столбца матрицы  равен сумме произведений соответствующих элементов
равен сумме произведений соответствующих элементов 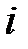 -й строки матрицы
-й строки матрицы  и
и  -го столбца матрицы
-го столбца матрицы 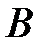 .
.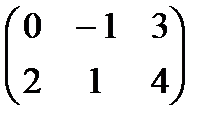 ,
,  =
= 
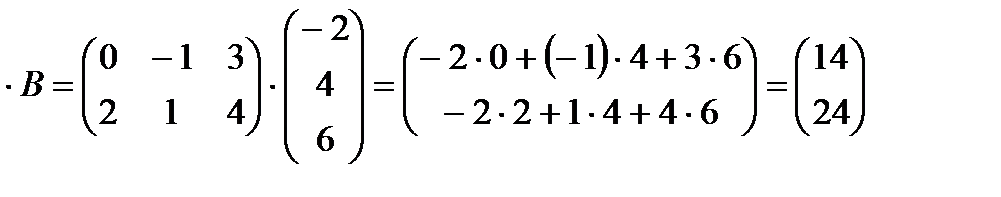
 – не существует.
– не существует.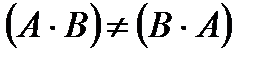 , даже если оба произведения определены.
, даже если оба произведения определены.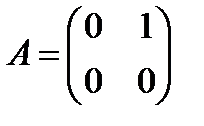 ,
, 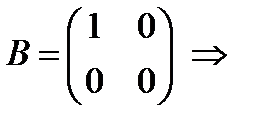
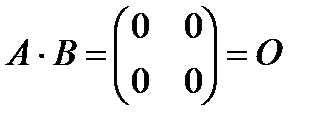 , хотя
, хотя 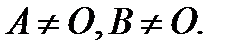

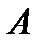 и
и  называются перестановочными, если
называются перестановочными, если 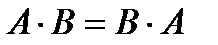 , в противном случае
, в противном случае 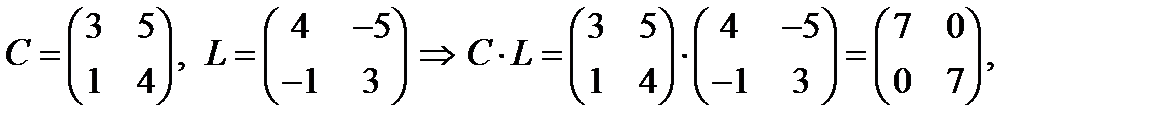

 матрицы
матрицы 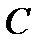 и
и 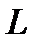 перестановочные.
перестановочные.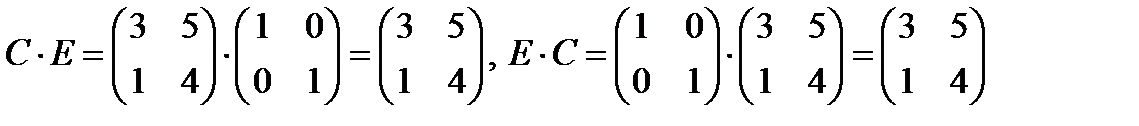 , то есть
, то есть 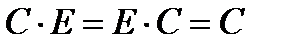 ,
,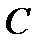 и
и 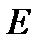 – перестановочные матрицы.
– перестановочные матрицы. . Это свойство матрицы
. Это свойство матрицы 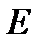 объясняет, почему именно она называется единичной: при умножении чисел таким свойством обладает число 1.
объясняет, почему именно она называется единичной: при умножении чисел таким свойством обладает число 1.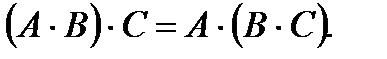
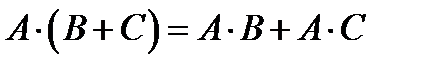 ,
, 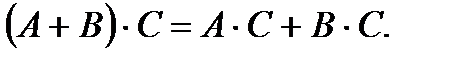
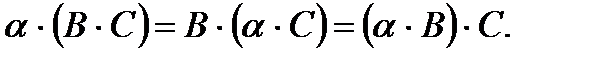
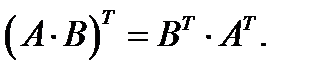
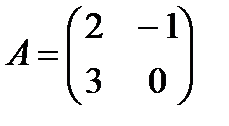 ,
, 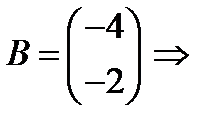
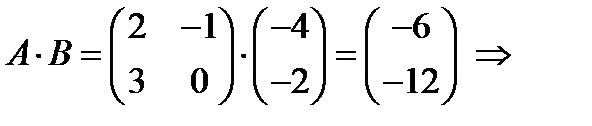
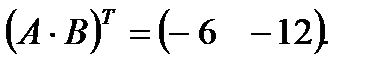

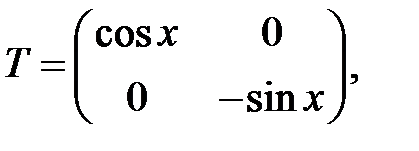
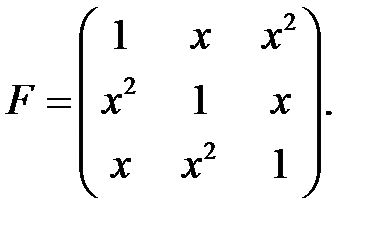

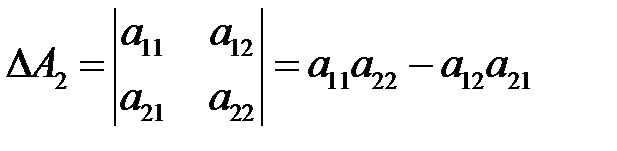 (1.1)
(1.1) или
или  .
.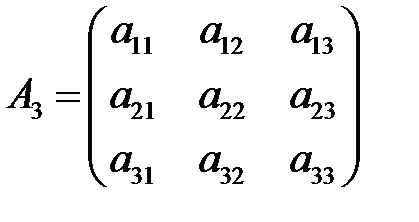 , которое вычисляется по правилу:
, которое вычисляется по правилу: (1.2)
(1.2)
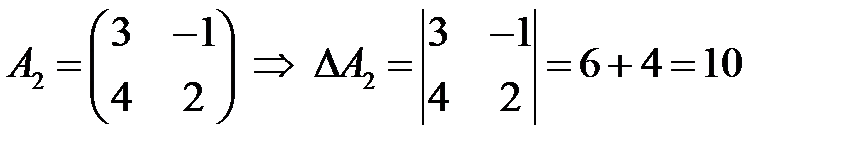 ;
; 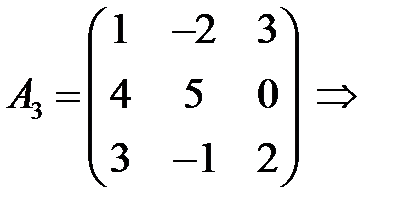
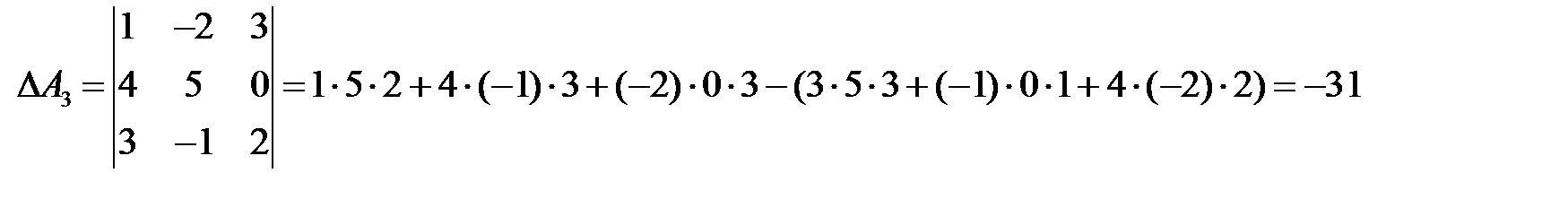
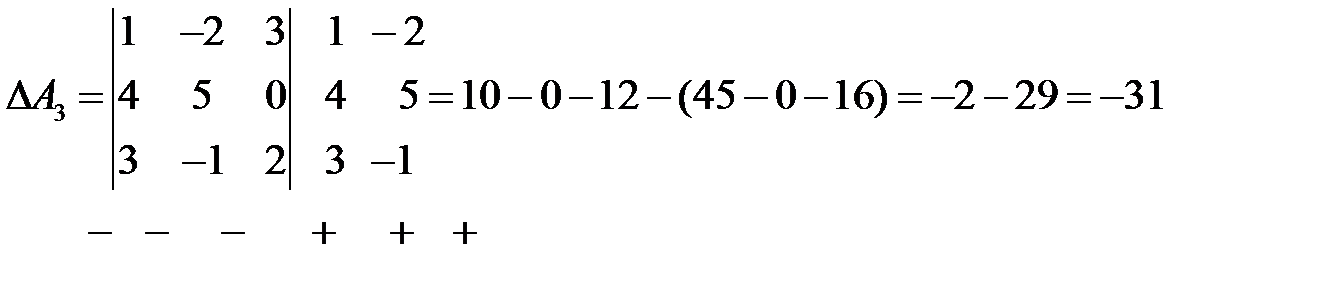
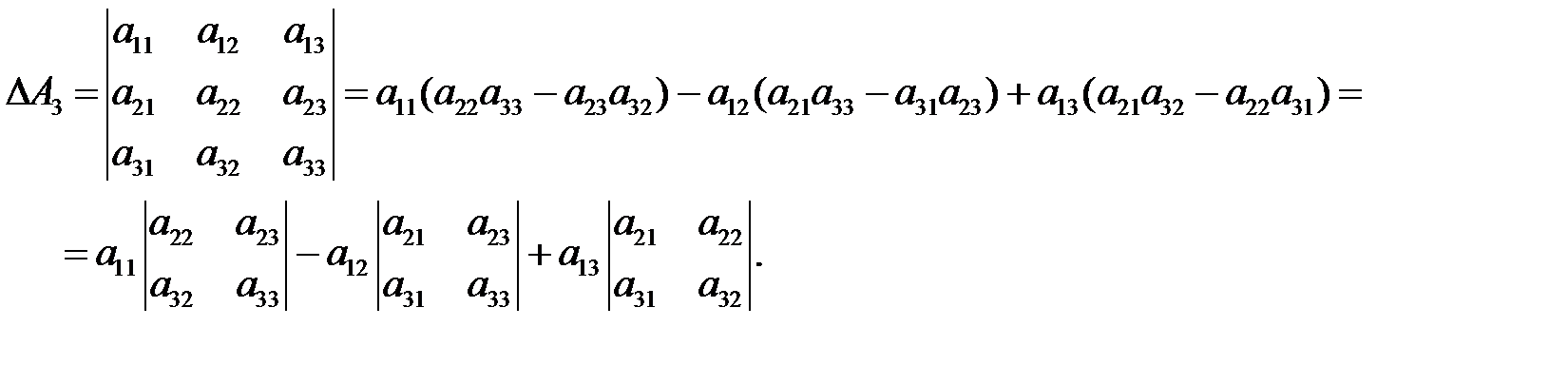 (1.3)
(1.3)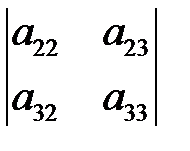 – определитель матрицы, полученный из
– определитель матрицы, полученный из  вычеркиванием элемента
вычеркиванием элемента 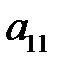 (точнее, первой строки и первого столбца, на пересечении которых стоит
(точнее, первой строки и первого столбца, на пересечении которых стоит 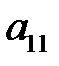 ),
), 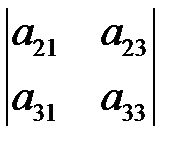 – вычеркиванием элемента
– вычеркиванием элемента 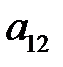 ,
,  – элемента
– элемента 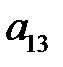 .
.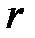 , что среди ее миноров
, что среди ее миноров  -го порядка есть хотя бы один ненулевой, а все миноры порядка (
-го порядка есть хотя бы один ненулевой, а все миноры порядка ( ) равны нулю.
) равны нулю.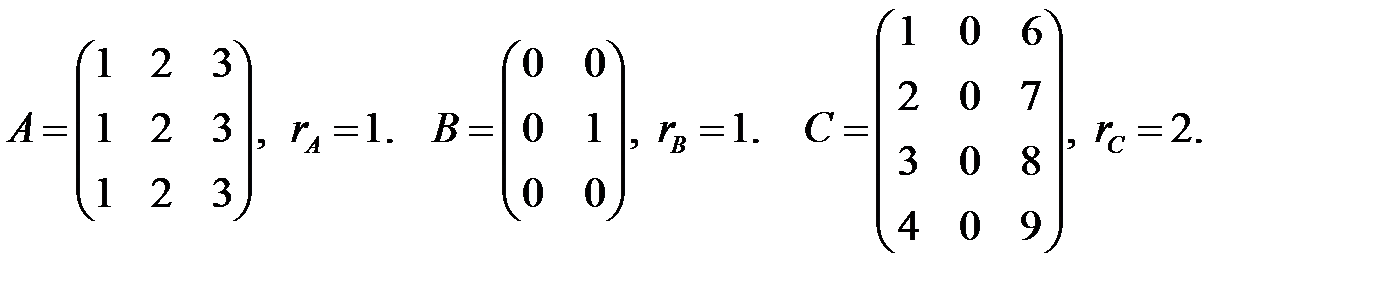
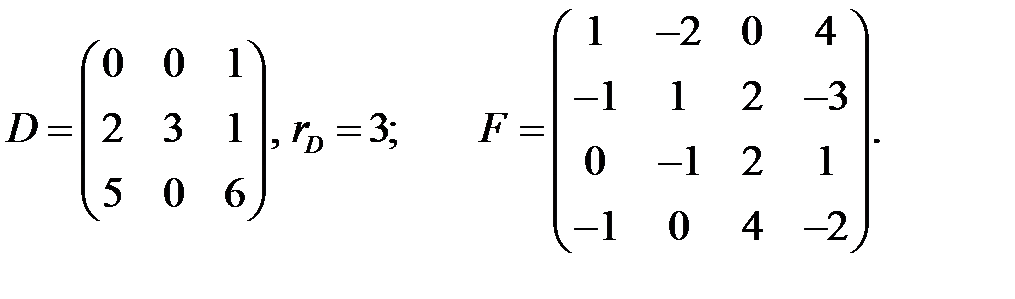
 , очевидно, имеет ненулевой минор второго порядка, например,
, очевидно, имеет ненулевой минор второго порядка, например,  , но все ее миноры третьего порядка – их всего 16 – равны нулю, поэтому
, но все ее миноры третьего порядка – их всего 16 – равны нулю, поэтому  Для того чтобы обнаружить этот факт без трудоемких вычислений, введем понятие элементарных преобразований.
Для того чтобы обнаружить этот факт без трудоемких вычислений, введем понятие элементарных преобразований. ;
; ;
;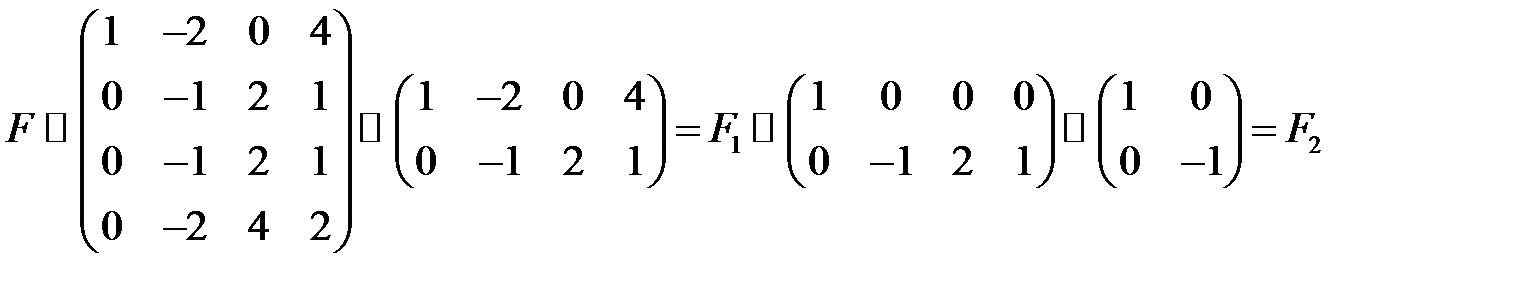 .
. к
к 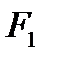 и
и 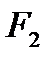 использовались элементарные преобразования 3), 5), 6): первую строку
использовались элементарные преобразования 3), 5), 6): первую строку  прибавили ко второй и четвертой, затем отбросили две из трех пропорциональных строк; далее первый столбец
прибавили ко второй и четвертой, затем отбросили две из трех пропорциональных строк; далее первый столбец  прибавили ко второму и четвертому с коэффициентами 2 и (-4) соответственно и два из трех пропорциональных столбцов отбросили. По теореме
прибавили ко второму и четвертому с коэффициентами 2 и (-4) соответственно и два из трех пропорциональных столбцов отбросили. По теореме  .
. , очевидно, можно было, получив лишь матрицу
, очевидно, можно было, получив лишь матрицу 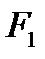 , не выполняя дальнейших преобразований.
, не выполняя дальнейших преобразований.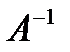 называется обратной для матрицы
называется обратной для матрицы 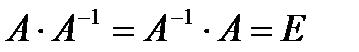 , где
, где 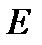 – единичная матрица.
– единичная матрица. – перестановочные, значит, обратная матрица существует лишь для квадратной матрицы
– перестановочные, значит, обратная матрица существует лишь для квадратной матрицы 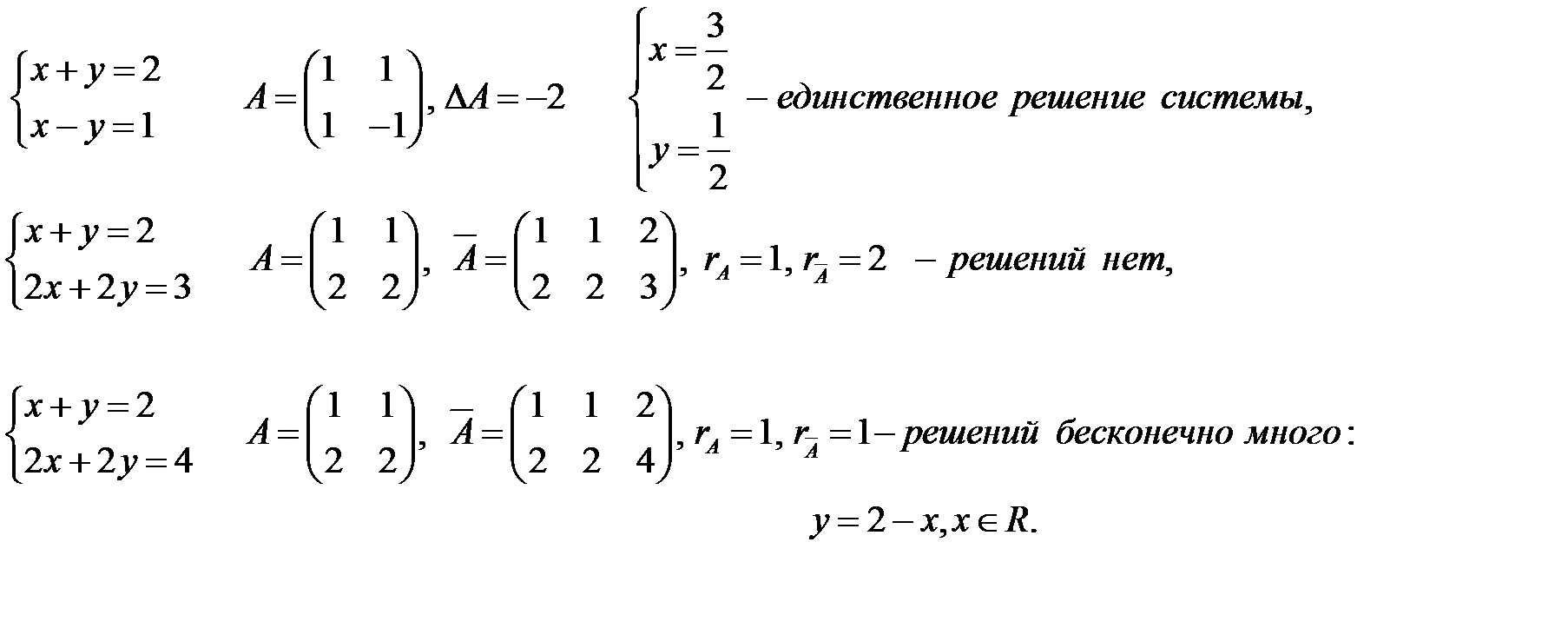
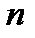 уравнений с
уравнений с 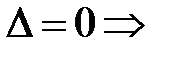 система имеет нетривиальное решение.
система имеет нетривиальное решение.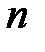 -го порядка равен нулю, то
-го порядка равен нулю, то 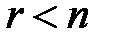 , значит, нетривиальное решение существует.
, значит, нетривиальное решение существует.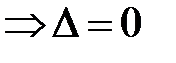 .
.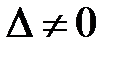 , то не равен нулю минор
, то не равен нулю минор 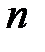 -го порядка основной матрицы, значит,
-го порядка основной матрицы, значит,  и решение единственно, что противоречит условию
и решение единственно, что противоречит условию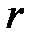 был меньше числа неизвестных
был меньше числа неизвестных 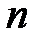 .
.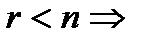 (1.15) имеет нетривиальное решение.
(1.15) имеет нетривиальное решение.
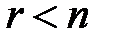 .
. , тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и
, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и 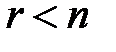 .
.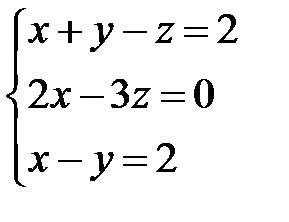

 , значит, систему матричным способом решить можно. Там же была найдена обратная матрица
, значит, систему матричным способом решить можно. Там же была найдена обратная матрица
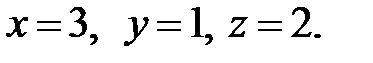 Проверкой убеждаемся, что решение найдено верно.
Проверкой убеждаемся, что решение найдено верно.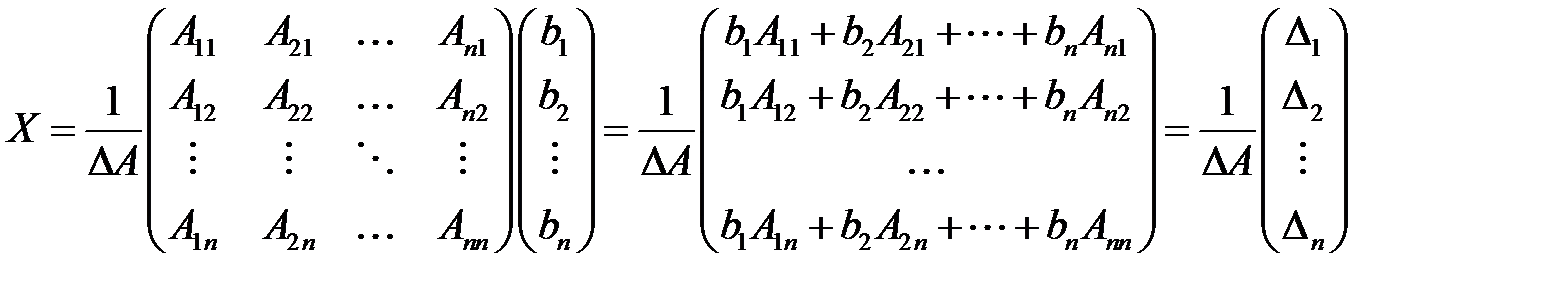 ,
, , (1.13)
, (1.13) ,
, 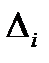 – определитель матрицы, полученной из А заменой ее
– определитель матрицы, полученной из А заменой ее  -го столбца на столбец правых частей системы (1.10),
-го столбца на столбец правых частей системы (1.10), 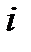 = 1,2,…,
= 1,2,…,  . Формулы (1.13) называются формулами Крамера.
. Формулы (1.13) называются формулами Крамера.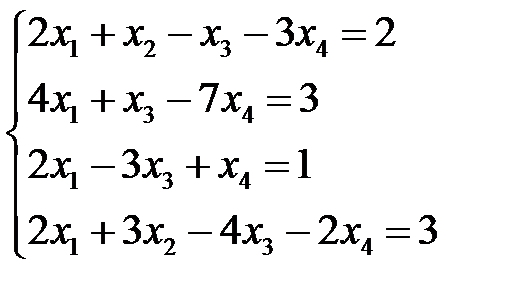 .
.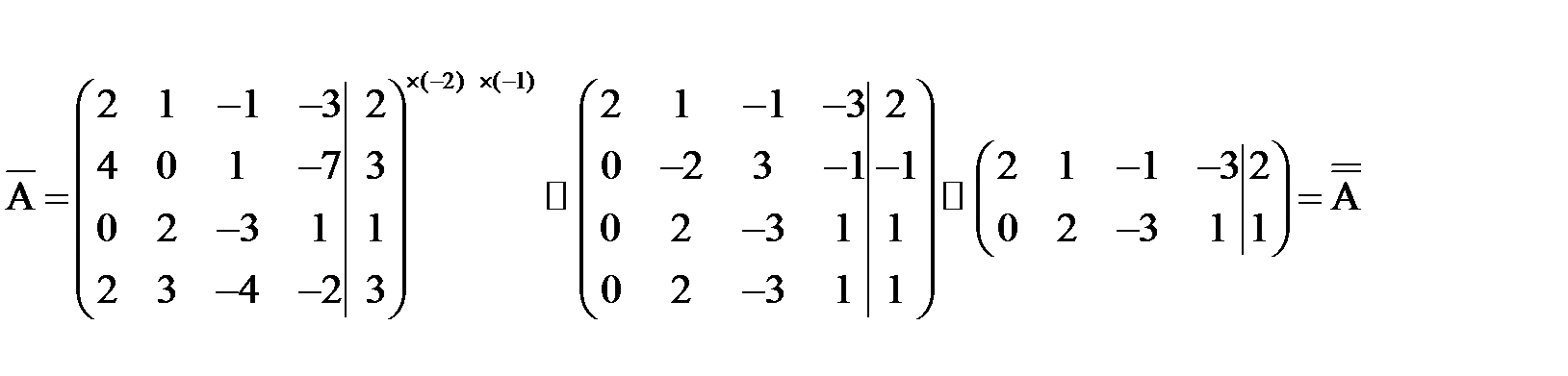
 по теореме
по теореме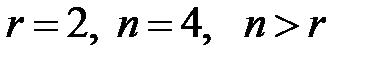 , значит, по теореме о числе решений система неопределенная, то есть имеет бесконечное множество решений и
, значит, по теореме о числе решений система неопределенная, то есть имеет бесконечное множество решений и 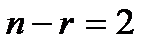 – число свободных переменных.
– число свободных переменных.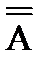 и эквивалентную исходной:
и эквивалентную исходной: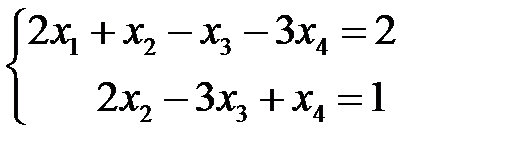 .
.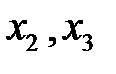 , считая их свободными (
, считая их свободными (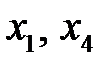 – зависимые переменные):
– зависимые переменные):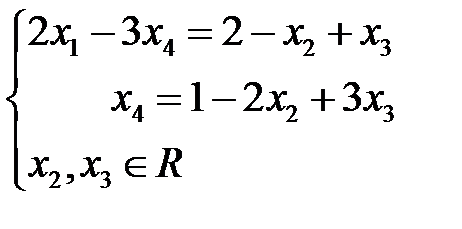 .
. в первое уравнение и выразим
в первое уравнение и выразим 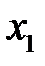 через свободные переменные:
через свободные переменные: – общее решение системы.
– общее решение системы. и
и  называются коллинеарными, если они лежат на параллельных прямых:
называются коллинеарными, если они лежат на параллельных прямых: 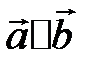 .
.


