Для бакалавров – заочников инженерного факультета 4 страницаДля этого сначала первую строку (все ее элементы!) умножим на (-2) и прибавим ко второй. Затем вновь первую строку умножим на (3) и прибавим к третьей. По свойству определителей от прибавления кратной строки определитель не меняется. Указанные преобразования обозначим следующим образом:
Полученный определитель, у которого во втором столбце лишь один ненулевой элемент, разложили по второму столбцу. Первая строка, которую мы умножали на числа и прибавили к другим (т.е. с которой мы работали), называется рабочей строкой, а элемент а12=1, с помощью которого мы получали нули во втором столбце, называется разрешающим элементом. Заметим, что это преобразование удобно для вычисления определителей высоких порядков. Например, вычислим определитель четвертого порядка:
Далее вычисляем определитель третьего порядка:
Пример 2 (к задачам 11-20). По формулам Крамера и методом Гаусса решить СЛАУ
Решение. Воспользуемся формулами Крамера:
Находим определитель матрицы системы разложением по первой строке:
Определитель Итак,
Ответ: х 1 = 0, х 2 = 1, х 3 = -2.
Решаем теперь методом Гаусса - расширенную матрицу А * приводим к ступенчатому виду с помощью элементарных преобразований, каковыми являются: 1. Перемена местами любых двух строк; 2. Умножение любой строки на любое число 3. Прибавление кратной строки. В результате получаем матрицу, эквивалентную (равносильную) данной; (~ - знак равносильности.)
Во-первых, обратим внимание на три числа: ранги матриц А и А * R(A), R (A *) и число неизвестных n. В нашем примере все преобразования, проводимые с матрицей А *, затрагивали одновременно и матрицу А - она отделена вертикальной чертой. Поэтому вместе с рангом матрицы А * видим и ранг матрицы А, подсчитав число ненулевых строк ступенчатой матрицы, которая отделена вертикальной чертой. Основополагающей теоретической базой является теорема Кронекера-Капелли, которую схематично можно записать так: R(A) = R(A *) = n R(A) = R(A *) < n R(A) < R(A *) Итак, в нашем примере R(A) = R(A *) = n = 3, следовательно, по теореме Кронекера-Капелли система имеет единственное решение. Для решения сопоставим ступенчатой матрице систему:
Как видим, система решается просто, «снизу вверх»: х 3 = – 2 и х 2 = 1. Подставляем в первое уравнение и получаем х 1 = 5 + х 3 – 3 х 2 = 5 – 2 – 3 = 0. Итак, система имеет единственное решение х 1 = 0, х 2 = 1, х 3 = – 2 – единственный вектор - решение
Найти: 1) косинус угла между ребрами АВ и АD; 2) площадь грани АВС; 3) объем пирамиды АВСD; 4) длину высоты пирамиды, проведенной из точки D. Решение. 1) Найдем координаты векторов
Итак, 2) Обозначим площадь грани, т.е. треугольника АВС, через S. Из определения векторного произведения получаем Найдем координаты вектора
Итак, 3) Для нахождения объема V пирамиды сначала заметим, что
Определитель разложили по первому столбцу (т.к. там имеется нуль). Смешанное произведение оказалось отрицательным, поэтому 4) Теперь легко определить высоту Н пирамиды, т.к.
Пример 4 (к задачам 31-40). Даны координаты четырех точек M (–1,1,–5), N (3,5, – 7), P (1,12, –15), Q (–1,3, – 4). Требуется: 1) составить уравнение прямой MN; 2) составить уравнение плоскости MNP; 3) составить уравнение прямой, проходящей через точку Q перпендикулярную плоскости MNP; 4) найти точку пересечения этой прямой с плоскостью MNP; 5) найти расстояние от точки Q до плоскости MNP (двумя способами). Решение. 1) Уравнение прямой МN напишем как уравнение прямой, проходящей через две точки
2) Уравнение плоскости MNP запишем как уравнение плоскости, проходящей через три точки:
3) Для написания уравнения прямой, проходящей через точку Q перпендикулярно плоскости MNP, воспользуемся уравнением прямой
- уравнение искомой прямой. 4) Обозначим точку пересечения полученной прямой с плоскостью MNP буквой R. Уравнение прямой QR запишем в параметрическом виде:
Подставим эти уравнения в уравнение плоскости MNP:
Итак, х = – 4/9 + 1 = 5/9; у = 8/9 + 3 = 35/9; z = 8/9 – 4 = – 28/9, т.е. получили координаты точки R(5/9;35/9; – 28/9). 5)Найдем теперь расстояние от точки Q до плоскости MNP двумя способами. Во-первых, это расстояние равно длине вектора
Во-вторых, воспользуемся формулой расстояния Н от точки М0(x0, y0, z0) до плоскости Ах + Ву + Сz + D = 0:
Получим:
Видим, что оба способа дают одинаковый результат.
Пример 5 (к задачам 41-50). Даны вершины треугольника MNP: М (–8, –3), N (4, –12), P (8,10). Требуется найти: 1) длину стороны MN; 2) уравнение сторон MN и NP и угловые коэффициенты; 3) угол N; 4) уравнение высоты РQ и её длину; 5) уравнение медианы МS. Решение. Сначала сделаем чертеж.
1) Длину стороны МN находим как длину вектора
2) Уравнения сторон МN и NP находим как уравнения прямых, проходящих через две точки: МN:
NP: Уравнение МN запишем в виде у + 3 = – 3/4(х +8), откуда находим её угловой коэффициент: КMN = – 3/4. Аналогично для прямой NP:
3) угол N треугольника находим с помощью скалярного произведения векторов
итак, Можно угол N находить с помощью угловых коэффициентов прямых NМ и NP, т.е. по формуле
РQ = Разумеется, к этому же результату можно придти по другому: можно найти координаты точки Q – пересечения МN и РQ, решив совместно их уравнения:
Применим формулы Крамера:
Итак, Q (–4; –6), тогда
5) Точка S – середина отрезка PN, её координаты находим по формуле:
Теперь через две точки напишем уравнение МS:
Пример 6 (к задачам 51-60). Вычислить Решение. Подставив х =2 получим неопределенность типа 0/0. Это означает, что многочлены х 2-3 х +2 и 3 х 3+ х 2-4 х -20 обращаются в нуль при х =2, т.е. х =2 является корнем обоих многочленов и оба многочлена делятся без остатка на (х -2). Проще всего деление осуществлять уголком:
x 2-3 x +2 ë_ x -2 _ 3 x 3+ x 2-4 x -20 ë x -2 - ï x -1 - ï 3 x 2+7 x +10 x 2-2 x 3 x 3-6 x 2 - x +2 7 x 2-4 x – – - x +27 x 2-14 x 0 10 x -20 – 10 x -20
Результатами делений являются равенства:
Теперь,
Пример 7 (к задачам 51-60). Вычислить Решение. Вновь имеем определитель типа 0/0, но в данном случае усложнение обусловлено наличием радикала: аргумент х «спрятан» под радикалом. Поскольку
Рассмотрим теперь случаи, когда Пример 8 (к задачам 51-60). Вычислить Решение. Имеем неопределенность типа
Мы учли, что
Пример 9 (к задачам 51-60). Вычислить Решение. При подстановке предельного значения аргумента х = 0 получаем неопределенность типа 0/0 и поскольку участвуют тригонометрические функции, следует применять 1-й замечательный предел: Тогда
Пример 10 (к задачам 51-60). Вычислить Решение. Подстановка предельного значения аргумента дает неопределенность типа
Заметим, что мы искусственно в скобках «подогнали» под формулу первого замечательного предела, в связи с чем нам пришлось домножить на
Пример 11 (к задачам 51-60). Вычислить Решение. Вспомним правило (см. пример 13), что при Теперь обратимся к заданному пределу. Общая формула второго замечательного предела означает, что под знаком предела стоит сумма единицы и некоторой бесконечно малой функции
Продолжаем «подгонять» под общую формулу второго замечательного предела. Получили в нашем случае Поэтому
Мы воспользовались тем, что
Пример 12 (к задачам 61-70). Найти производную функции Решение.
|





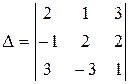








 .
.





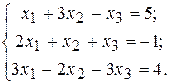
 ,
,  ,
,  .
.
 , следовательно, можно использовать выбранный метод решения. Вычисляем вспомогательные определители:
, следовательно, можно использовать выбранный метод решения. Вычисляем вспомогательные определители: ,
,

 получен из
получен из  заменой i-го столбца столбцом свободных членов.
заменой i-го столбца столбцом свободных членов.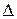 = 33,
= 33, 
 , отличное от нуля;
, отличное от нуля;




 .
. система имеет единственное решение;
система имеет единственное решение;
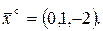
 Пример 3 (к задачам 21-30). Даны координаты пирамиды АВСD (рис); А (1,-4,0), В (5,0,-2), С (3,7,-10), D (1,-2,1).
Пример 3 (к задачам 21-30). Даны координаты пирамиды АВСD (рис); А (1,-4,0), В (5,0,-2), С (3,7,-10), D (1,-2,1). и
и  , вычитая из координат конца вектора координаты начала. Получим:
, вычитая из координат конца вектора координаты начала. Получим: 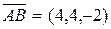 ,
,  . Тогда, обозначив угол между ними через
. Тогда, обозначив угол между ними через  , имеем
, имеем .
. .
. , т.к. длина векторного произведения равна площади параллелограмма, т.е. удвоенной площади треугольника.
, т.к. длина векторного произведения равна площади параллелограмма, т.е. удвоенной площади треугольника. . По формуле для векторного произведения в координатной форме находим:
. По формуле для векторного произведения в координатной форме находим:
 .
. , тогда
, тогда  , следовательно, S = 27.
, следовательно, S = 27. , где V 1 – объем параллелепипеда, построенного на векторах
, где V 1 – объем параллелепипеда, построенного на векторах 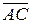 , а для вычисления V 1 используется смешанное произведение этих векторов:
, а для вычисления V 1 используется смешанное произведение этих векторов: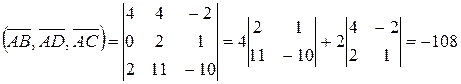 .
.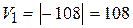 , а V =1/6
, а V =1/6  . Итак, V =18.
. Итак, V =18.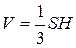 , откуда
, откуда . Итак, Н = 2.
. Итак, Н = 2.
 или MN:
или MN:  .
.

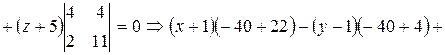


 с опорной точкой (x 0, y 0, z 0) и направляющим вектором
с опорной точкой (x 0, y 0, z 0) и направляющим вектором  =(
=( ), взяв точку Q в качестве опорной точки, а в качестве направляющего вектора
), взяв точку Q в качестве опорной точки, а в качестве направляющего вектора  =(1,-2,-2). Тогда получим:
=(1,-2,-2). Тогда получим:

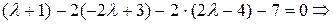 9
9  = – 4,
= – 4,  :
: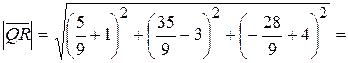
 .
.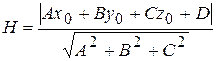 .
. .
.
 =(4 – (– 8); – 12 – (– 3))=(12;9):
=(4 – (– 8); – 12 – (– 3))=(12;9): 
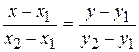 .
. .
.

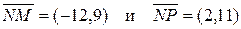 :
: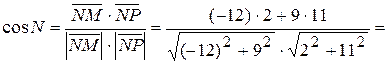

 .
.
 4) уравнение высоты РQ напишем по формуле у – у 0 = k (х – х 0), воспользовавшись условием перпендикулярности прямых РQ и МN:
4) уравнение высоты РQ напишем по формуле у – у 0 = k (х – х 0), воспользовавшись условием перпендикулярности прямых РQ и МN:  ,
, .
.

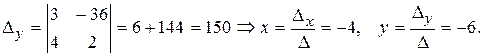
 = (–12; –16),
= (–12; –16),

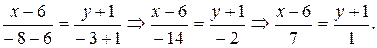
 .
. ;
;  .
.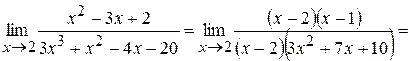


 и простейшим источником неопределенности является (х - 5). Этот множитель уже имеется в знаменателе, а в числителе его нужно получить. Для этого применяются искусственные приемы. В данном случае домножим числитель и знаменатель на выражение (
и простейшим источником неопределенности является (х - 5). Этот множитель уже имеется в знаменателе, а в числителе его нужно получить. Для этого применяются искусственные приемы. В данном случае домножим числитель и знаменатель на выражение (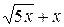 ), сопряженное числителю с тем, чтобы для избавления от иррациональности в числителе использовать формулу разности квадратов: (а - b)(а + b) = а 2 - b 2. Получим:
), сопряженное числителю с тем, чтобы для избавления от иррациональности в числителе использовать формулу разности квадратов: (а - b)(а + b) = а 2 - b 2. Получим:

 .
.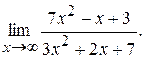
 и поскольку сам аргумент
и поскольку сам аргумент  .
.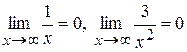 т.д.
т.д. .
.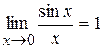 . На практике чаще всего первый замечательный предел применяется в более общей формулировке: пусть
. На практике чаще всего первый замечательный предел применяется в более общей формулировке: пусть  и при этом функция
и при этом функция 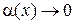 , тогда
, тогда 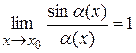 . Теперь переходим к вычислению указанного предела. Воспользуемся формулой
. Теперь переходим к вычислению указанного предела. Воспользуемся формулой  .
.
 .
. .
. . Кроме того, аргумент стремится к двум (
. Кроме того, аргумент стремится к двум ( ), а не к нулю. В таких случаях удобно провести замену переменной у=2-х и если
), а не к нулю. В таких случаях удобно провести замену переменной у=2-х и если  . Оформим это следующим образом:
. Оформим это следующим образом: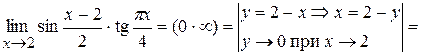


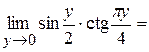

 .
. .
. .
.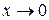 предел отношения двух многочленов одинаковой степени равен отношению их старших коэффициентов, и получим в данном примере неопределенность типа
предел отношения двух многочленов одинаковой степени равен отношению их старших коэффициентов, и получим в данном примере неопределенность типа  . Поскольку фигурирует показательная функция, то раскрывать эту неопределенность следует с помощью второго замечательного предела
. Поскольку фигурирует показательная функция, то раскрывать эту неопределенность следует с помощью второго замечательного предела  , или
, или 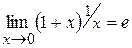 , где
, где  . Второй замечательный предел применяется в более общей формулировке: пусть
. Второй замечательный предел применяется в более общей формулировке: пусть  ) и при этом функция
) и при этом функция  , тогда
, тогда 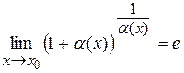 .
. , а в показателе степени находится
, а в показателе степени находится  . Вот и «подгоним» заданный предел под форму второго замечательного предела (добавив и отняв единицу):
. Вот и «подгоним» заданный предел под форму второго замечательного предела (добавив и отняв единицу):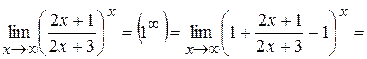
 .
. , следовательно
, следовательно  .
.
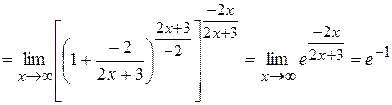 .
. .
. .
. можно расматривать, как функцию, зависящую от некоторой переменной u:
можно расматривать, как функцию, зависящую от некоторой переменной u:  , где u также является некоторой функцией
, где u также является некоторой функцией  , а
, а  . По правилу дифференцирования сложной функции можем записать:
. По правилу дифференцирования сложной функции можем записать:


