Для бакалавров – заочников инженерного факультета 7 страница
Пример 24 (к задачам 171-180) Найти общее решение дифференциального уравнения (ДУ): Решение: Нахождение интегральной кривой для ДУ, проходящей через заданную точку, сводится к решению задачи Коши. Решить задачу Коши означает найти такое частное решение ДУ, которое удовлетворяет заданным начальным условиям. Для ДУ первого порядка начальные условия имеют вид y (xo) = yo, т.е. требуется найти такое частное решение ДУ y (x), которое удовлетворяет условию: y= yo, при х=хо. Это означает, что требуется найти такую функцию y(x), график которой (он называется интегральной кривой) проходит через точку с координатами (xo, yo). Обратимся теперь к заданному ДУ. При решении ДУ в первую очередь следует определить к какому типу ДУ относится заданное ДУ и в соответствии с этим избрать метод решения. Несколько преобразуем наше ДУ:
Теперь ясно, что это линейное дифференциальное уравнение (ЛДУ) 1-го порядка. Действительно, общий вид ЛДУ 1-го порядка следующий: у’ + p (x) y = q (x), так что в нашем примере
Для нахождения общего решения ЛДУ 1-го порядка обычно применяют один из двух методов: метод вариации произвольного постоянного (иначе его называют методом Лагранжа) и метод двух функций (иначе его называют методом Бернулли). Мы решим заданное ДУ обеими способами и читатель увидит, что в практическом плане оба метода не сильно отличаются, однако, «идеология» у них разная. 1 ) Метод двух функций (Метод Бернулли). Идея метода не нова – свести решение задачи к двум задачам, но более простым. Такой прием уже применялся, например, при интегрировании по частям. Итак, решение ДУ будем искать в виде произведения двух функций:
Подставляем эти выражения в заданное ДУ:
Приравняем скобку нулю:
Легко заметить, что мы получили линейное однородное ДУ (ЛОДУ), соответствующее заданному неоднородному ДУ (ЛНДУ). Всякое ЛОДУ 1-го порядка является ДУ с разделяющими переменными. Разделяя переменные и интегрируя, получим какое-нибудь частное решение:
Теперь подставим полученное выражение для функции v в ДУ (6):
Итак, окончательно,
2) Метод вариации производной постоянной (Метод Лагранжа). Лагранж предложил общее решение ЛНДУ искать в виде общего решения соответствующего ЛОДУ, только вместо произвольного постоянного С взять функцию С (х), которую и следует найти. Сначала решаем ЛОДУ, соответствующее заданному ЛНДУ:
Итак, В соответствии с предложением Лагранжа общее решение ЛНДУ ищем в виде
отсюда получаем: следовательно,
Как видим, оба метода дали одинаковые результаты. Приступаем теперь к нахождению частного решения, удовлетворяющего заданному начальному условию у (2) = 2. Для этого надо в общее решение подставить х = 2 и у = 2 и затем найти Итак,
Пример 25 (к задачам 171-180). Найти общее решение ДУ Решение: Известно, что у – общее решение ЛНДУ представляется в виде суммы
1-й метод (метод вариации произвольных постоянных). Сначала решаем соответствующее ЛОДУ:
Следовательно, Частное решение ЛНДУ записываем в виде:
Полагаем скобку равной нулю
и в этом предположении находим
Подставляем теперь полученные выражения в исходное ДУ:
Слагаемые, содержащие
Определитель этой системы (он называется определителем Вронского или вронскианом) отличен от нуля:
. Находим вспомогательные определители:
Следовательно, по формулам Крамера имеем:
Остается найти интегралы:
Произвольную постоянную в неопределенном интеграле взяли равной нулю, т.к. требуется какое-нибудь одно частное решение.
Итак,
2-ой метод (метод неопределенных коэффициентов). Иначе этот метод называется подбором ỹ; по виду правой части. Заметим, что первый метод является универсальным, какова бы ни была правая часть ЛНДУ. Второй метод имеет ограниченное применение: если только правая часть ЛНДУ f (х) имеет вид:
где
где – S = max(m, n), Qs (х), Rs (х) – многочлены степени S с неопределенными коэффициентами (которые и требуется найти), r – кратность числа α + βj в качестве корня характеристического уравнения. Этот, на первый взгляд громоздкий алгоритм, на практике таковым не является. Действительно, обратимся к заданному уравнению Остается найти А и В. Для этого подставим
Следовательно,
Приводим подобные члены:
Приравниваем соответствующие коэффициенты при синусе и косинусе:
И общее решение ЛНДУ имеет вид:
Результаты, естественно, совпали; однако трудоемкость методов существенно разнится.
.
Пример 26 (к задачам 181-190). Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала Решение. Для нахождения интервала сходимости степенного ряда воспользуемся признаком Даламбера: l= Если l<;1, то ряд сходится, если l >;1, - ряд расходится, если l= 1 – признак ответа не дает. Находим интервал сходимости:
Итак, на интервале (0;6) ряд сходится, вне этого интервала – расходится, а в точках х = 0 и х = 6 требуется дополнительное исследование. а) Пусть х = 0, тогда степенной ряд становится числовым:
Это знакочередующийся ряд, причем
б) Пусть х = 6, тогда получим ряд
Ответ. Интервал сходимости:
Пример 27 (к задачам 191-200). С точностью до 0,001 вычислить определенный интеграл разложением подынтегральной функции в ряд Маклорена: Решение. Воспользуемся разложением в ряд Маклорена функции sin x: sin x = х sin Как известно, степенной ряд можно почленно интегрировать, при этом радиус сходимости не меняется. Поэтому
Получили знакочередующийся ряд. Теорема Лейбница утверждает, что если для приближенного вычисления суммы ряда ограничиться несколькими первыми членами, то совершаемая при этом ошибка не превосходит (по абсолютной величине) первого из отброшенных членов. Вопрос теперь лишь в том, сколькими членами ряда достаточно ограничиться, чтобы обеспечить заданную точность. Рассуждаем методом перебора. Если ограничиться лишь первым членом ряда, то ошибка не превзойдет числа Итак, с точностью до 0,001, получаем:
Пример 28 (к задачам 191-200) Найти три первых отличных от нуля члена разложения в ряд Тейлора решения задачи Коши
Решение. В данном примере нам требуется найти частное решение В соответствии с заданным начальным условием
Коэффициенты разложения находим поочерёдно. Первый коэффициент есть начальное условие:. Второй коэффициент найдём из данного уравнения, переписав его в виде Итак, получили три первых отличных от нуля, члена разложения в ряд Тейлора решения задачи Коши: В данном примере можно наглядно сравнить приближенное и точное решения. Уравнение является ЛНДУ І порядка. Решив его, получим частное решение, удовлетворяющее заданному условию: Точное и приближенное решения изображены на рисунке:
Пример №29 (к задачам 201-210). В результате опыта могут произойти три независимых события А1,А2, и А3 с вероятностями Р (А 1) = 0,9, Р (А 2) = 0,8, Р (А 3) = 0,1. Найти вероятности того, что в результате опыта: 1) произойдут все три события; 2) произойдет хотя бы одно событие; 3) произойдет ровно одно событие; 4) произойдет только первое событие. Решение. 1) Обозначим событие В = (в результате опыта произойдут все три события). Иначе говоря, в результате опыта произойдет А 1
Р (В) = Р (А 1 • А 2 • А 3) = Р (А 1) • Р (А 2) • Р (А 3) = 0,9 • 0,8 • 0,1 = 0,072;
Таким образом, Р (В) = 0,072.
2) Обозначим событие С = (в результате опыта произойдет хотя бы одно из событий А 1, А 2, А 3). Другими словами событие с означает, что в результате опыта произойдет или А 1 или А 2 или А 3. Поскольку произносится союз или, то это указывает на то, что события складываются: С = А 1 + А 2 + А 3. При этом необходимо учитывать, что здесь союз или произносится не совсем в обыденном употреблении, когда иногда применение союза или к А и В предполагает исключение одного из другого. В теории вероятностей сумма двух событий А+В означает: или А или В или оба. Поэтому теорема сложения вероятностей имеет вид: Р (А + В) = Р (А) + Р (В) – Р (А • В), а для трех событий
Р (А 1 + А 2 + А 3) = = Р (А 1) + Р (А 2) + Р (А 3) – Р (А 1 • А 2) – Р (А 1• А 3) – Р (А 2 • А 3) + Р (А 1 • А 2 • А 3).
Для нашего примера
Р (С) = Р (А 1 + А 2 + А 3) = = 0,9 + 0,8 + 0,1 – 0,9 • 0,8 – 0,9 • 0,1 – 0,8 • 0,1 + 0,9 • 0,8 • 0,1 = 0,982.
Как видим, формула получилась громоздкой. В таких случаях следует всегда иметь в виду нахождение противоположного события и его вероятности. Противоположным событием
Р (
то Р (С)=1 – Р( 3) Обозначим: D = (в результате опыта произойдет ровно одно событие), т.е. D =
4) Обозначим: Е = (в результате опыта произойдет только событие А 1), т.е. Е =
Пример №30 (к задачам 211-220). В коробке лежат неотличимые по внешнему виду два игральных кубика: один правильный, а второй – неправильный, у которого шестерка выпадает с вероятностью 1/3, пятерка- с вероятностью 1/6, а остальные- с одинаковыми вероятностями. Из коробки наудачу берут и подбрасывают кубик. Какова вероятность того, что выпадет шестерка. Решение. Это пример на применение формулы полной вероятности, когда исследуемое событие А происходит с одним из событий (гипотез)
Поскольку кубики неотличимы по внешнему виду, то Р (А) = Р (Н 1) Условные вероятности даны в задаче:
|

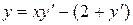 .Для заданного уравнения найти интегральную кривую, проходящую через точку (2, 2).
.Для заданного уравнения найти интегральную кривую, проходящую через точку (2, 2).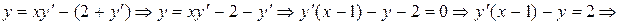
 .
.
 .
. или
или  (6)
(6) .
.
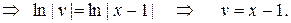
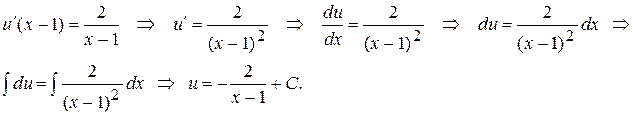
 – общее решение заданного ЛНДУ.
– общее решение заданного ЛНДУ.
 – общее решение ЛОДУ.
– общее решение ЛОДУ.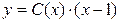 , где функцию с(х) требуется найти. Для этого подставляем
, где функцию с(х) требуется найти. Для этого подставляем  ,
, или
или 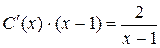 ,
, и
и  ,
, – общее решение ЛНДУ.
– общее решение ЛНДУ. .
. , т.е.
, т.е.  – решение задачи Коши. Графически это решение задаёт кривую, проходящую через точку (2, 2).
– решение задачи Коши. Графически это решение задаёт кривую, проходящую через точку (2, 2). .
. – общего решения ЛОДУ и ỹ; - какого-нибудь частного решения ЛНДУ. Частное решение ỹ; можно находить двумя способами:
– общего решения ЛОДУ и ỹ; - какого-нибудь частного решения ЛНДУ. Частное решение ỹ; можно находить двумя способами: . Составляем характеристическое уравнение
. Составляем характеристическое уравнение .
. – общее решение ЛОДУ.
– общее решение ЛОДУ.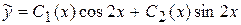 . Для нахождения функций
. Для нахождения функций  и
и  подставим
подставим 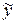 в исходное ДУ. Предварительно найдем
в исходное ДУ. Предварительно найдем
 (7)
(7)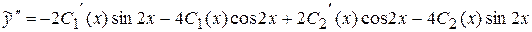 .
.
 .
. и
и 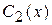 уничтожаются. Тогда последнее уравнение вместе с уравнением (7) образуют систему уравнений для нахождения
уничтожаются. Тогда последнее уравнение вместе с уравнением (7) образуют систему уравнений для нахождения 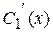 и
и  :
:
 ;
;  .
. и
и  .
.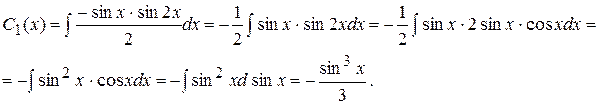

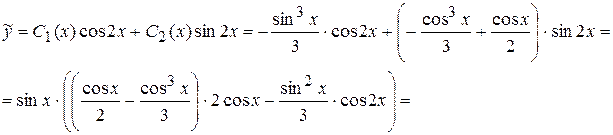



 , (8)
, (8) и
и  ) – многочлены степени т и п соответственно. В этом случае
) – многочлены степени т и п соответственно. В этом случае  ищем в виде:
ищем в виде: , (9)
, (9) . Корни характеристического уравнения мы нашли ранее:
. Корни характеристического уравнения мы нашли ранее:  . Правая часть
. Правая часть  является частным случаем формулы (8) при α = 0, β = 1, следовательно, α; + βj = j и это число не является корнем характеристического уравнения. Это означает, что кратность r = 0. Коэффициент при синусе равен 1, т.е. является многочленом нулевой степени, поэтому и в формуле (9) коэффициенты при косинусе и синусе будут многочленами нулевой степени (т.е. некоторыми числами А и В). Итак, в нашем случае
является частным случаем формулы (8) при α = 0, β = 1, следовательно, α; + βj = j и это число не является корнем характеристического уравнения. Это означает, что кратность r = 0. Коэффициент при синусе равен 1, т.е. является многочленом нулевой степени, поэтому и в формуле (9) коэффициенты при косинусе и синусе будут многочленами нулевой степени (т.е. некоторыми числами А и В). Итак, в нашем случае  .
.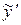 и
и  :
: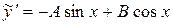 ;
;  .
. .
. .
.
 .
. .
.
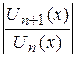 =
=  =
=  =
= 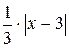 .
.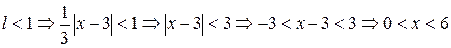 .
. =
=  =
=  =
=  -
-  , следовательно, по признаку Лейбница ряд расходится.
, следовательно, по признаку Лейбница ряд расходится. =
=  =
= 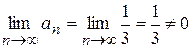 , следовательно, по необходимому признаку ряд расходится.
, следовательно, по необходимому признаку ряд расходится. .
. .
.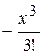 +
+ 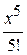
 +…. и заменим х на
+…. и заменим х на  :
:
 +
+ 
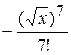 +….
+….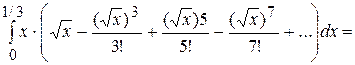
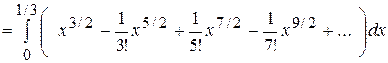 =
= 

 .
. =
=  . Это больше требуемого значения 0,001. Для первого и второго членов ряда ошибка будет значительно меньше 0,001.
. Это больше требуемого значения 0,001. Для первого и второго членов ряда ошибка будет значительно меньше 0,001.

 Найти точное решение. Сравнить результаты на чертеже.
Найти точное решение. Сравнить результаты на чертеже. данного дифференциального уравнения, удовлетворяющего начальным условиям
данного дифференциального уравнения, удовлетворяющего начальным условиям  , приближенно, определив три первых (отличных от нуля) члена разложения этого решения в ряд Тейлора.
, приближенно, определив три первых (отличных от нуля) члена разложения этого решения в ряд Тейлора.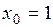 , т.е. по степеням
, т.е. по степеням  :
:
 , откуда
, откуда  ,
,  . Следующие коэффициенты находим последовательным дифференцированием данного уравнения:
. Следующие коэффициенты находим последовательным дифференцированием данного уравнения: 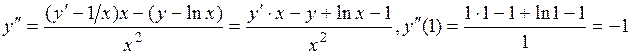
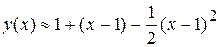 .
. .
.
 А 2
А 2  для С является:
для С является:  . Поскольку
. Поскольку . В этой сумме все слагаемые попарно несовместные, за счет присутствия в каждом слагаемом противоположных событий. Поэтому
. В этой сумме все слагаемые попарно несовместные, за счет присутствия в каждом слагаемом противоположных событий. Поэтому
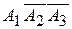 , следовательно, Р (Е) = Р (
, следовательно, Р (Е) = Р (
 ,
,  …,
…,  , т.е. опыт как разбивается на два этапа: сначала происходит одна из гипотез, а затем событие А. В нашем случае надо выбрать кубик, а затем подбросить его и ждать появится или нет шестерка. Поэтому обозначим гипотезы:
, т.е. опыт как разбивается на два этапа: сначала происходит одна из гипотез, а затем событие А. В нашем случае надо выбрать кубик, а затем подбросить его и ждать появится или нет шестерка. Поэтому обозначим гипотезы: .
.



