Алгоритм метода Гаусса с выбором главного элемента по столбцам.
1. Для m = 1, 2, …, n – 1 выполним преобразования: Найдем максимальный по абсолютной величине элемент в m -ом столбце. Пусть это будет элемент aim. Если i ≠ m, то меняем местами i -ую и m -ую строки:
r = aij, aij = amj, amj = r, j = 1, …, n; r = bi, bi = bm, bm = r.
Элементы матрицы и вектора после преобразования на m -ом шаге обозначим Делим m -ое уравнение на ведущий элемент
а затем исключаем переменную xm с помощью m -ого уравнения из i -го,
2. Вычисляем неизвестные xi в обратном порядке:
Приведенный вариант метода Гаусса дает решение и тогда, когда обычный метод Гаусса перестает работать из-за деления на ноль. При реализации метода Гаусса на каком-либо языке программирования удобно использовать исходные матрицу a и вектор b для хранения промежуточных результатов преобразований. Приведенные формулы преобразований записываются как операторы присваивания, т.е. имена переменных aij и bj записываются без верхних индексов. Ниже приведены различные примеры программ метода Гаусса. В другом варианте метода, методе Гаусса с выбором главного элемента по строкам на каждом шаге выбирают наибольший по модулю элемент строки и переставляют столбцы так, чтобы ведущий элемент находился на диагонали. В этом варианте метода Гаусса в уравнениях неизвестные переменные меняются местами и в алгоритме надо заботиться о том, чтобы запомнить эти перестановки. В общем случае метода Гаусса с выбором главного элемента на шаге m ищется максимальный по модулю элемент во всей матрице коэффициентов, и производится перестановка строк и столбцов так, чтобы этот элемент стал диагональным. Мы не будем рассматривать реализации указанных вариантов метода Гаусса. Отметим, что последний вариант метода Гаусса с выбором главного элемента считается лучшим. Общее число операций для решения системы уравнений методом Гаусса составляет приблизительно [1] 2 n 3/3 + 2 n 2, при этом большая часть, т.е. 2 n 3/3 операций приходится на прямой ход. Пример 3.3. Решить методом Гаусса систему уравнений 4 x 1 + 2 x 2 – 4 x 3 + 2 x 4 = 12, 2 x 1 + 9 x 2 – 4 x 3 – 4 x 4 = 14, 3 x 1 + 2 x 2 – 8 x 3 + 2 x 4 = 20, 4 x 1 + 2 x 2 + 5 x 3 + 7 x 4 = 10. Решение. Продемонстрируем решение в программе электронных таблиц. 0. Запишем коэффициенты и правые части системы в диапазоне A 1: E 4. 1. В диапазоне A 5: E 8 сформируем расширенную матрицу системы, которая получится после исключения переменной x 1 из второго, третьего и четвертого уравнений. В ячейку A 5 вводим формулу =A1/$A1; выделим A 5 и протянем маркер заполнения (мышью за правый нижний угол) до E 5. Затем в ячейку A 6 вводим формулу =A2-A$5*$A2; выделим A 6 и протянем маркер заполнения до E 6. Выделим диапазон A 6: E 6 и протянем маркером заполнения до E 8. В ячейках A 5: E 8 появятся следующие значения:
2. В диапазоне A 9: E 12 сформируем матрицу системы, которая получится после исключения x 2 из третьего и четвертого уравнений. Присвоим строке A 9: E 9 значения строки A 5: E 5, т.е. выделим диапазон A 9: E 9 и введем формулу =A5:E5 и удерживая нажатыми клавиши Ctrl и Shift, нажимаем Enter. В ячейку B 10 вводим формулу =B6/$B6; выделим B 10 и протянем маркер заполнения до E 10. Затем в ячейку B 11 вводим формулу =B7-B$10*$B7; выделим B 11 и протянем мышью маркер заполнения до E 11. Выделим диапазон B 11: E 11 и протянем маркер заполнения до E 12. В ячейках A 9: E 12 появятся следующие значения:
3. В диапазоне A 13: E 16 сформируем матрицу системы, которая получится после исключения x 3 из четвертого уравнения. Перепишем значения строк A 9: E 10 в строки A 13: E 14, для этого выделим диапазон A 13: E 14 и введем формулу =A9:E10 и удерживая клавиши Ctrl и Shift нажатыми, нажимаем Enter. В ячейку C 15 вводим формулу =C11/$C11; выделим C 15 и протянем мышью за правый нижний угол до E 15. В ячейку C 16 вводим формулу =C12-C$15*$C12, выделим C 16 и протянем мышью за правый нижний угол до E 16. В ячейках A 13: E 16 получим значения:
4. Сформируем в диапазоне A 17: E 20 окончательную матрицу системы, которая имеет треугольный вид с единицами на диагонали. Выделим диапазон A 17: E 19 и введем формулу =A13:E15 и, удерживая нажатыми клавиши Ctrl и Shift, нажимаем Enter. В ячейку D 20 вводим формулу =D16/$D16, выделим C 15 и протянем мышью за правый нижний угол до E 20. В диапазоне A 17: E 20 получим:
В таблице 3.1 показаны введенные формулы, которые можно увидеть, если выполнить команду меню «Сервис — параметры», выбрать вкладку «Вид» и отметить в параметрах окна флажком пункт «формулы». 5. Теперь остается выполнить обратный ход метода Гаусса. Для этого в ячейках F 17: F 20 введем формулы:
В ячейках F 17: F 20 получим ответ: x 1 = –1,1677; x 2 = 2,2446; x 3 = –1,7081; x 2 =2,6746.
Таблица 3.1
В таблице 3.2 приведены результаты решения системы (после снятия флажка с пункта «формулы» меню «Сервис — параметры»). Таблица 3.2
6. Для проверки правильности введенных формул умножим исходную матрицу коэффициентов, хранящихся в ячейках A 1: D 4, на столбец найденных решений F 17: F 20, и запишем полученные значения в столбец F 1: F 4. Для этого выделим диапазон F 1: F 4, введем формулу =МУМНОЖ(A1:D4;F17:F20) и, удерживая нажатыми клавиши Ctrl и Shift, нажмем Enter. Значения в столбцах E 1: E 4 и F 1: F 4 должны совпадать. Замечание. Приведенный лист с формулами можно применить для решения любой системы уравнений с четырьмя неизвестными. Для этого в диапазоне A 1: E 4 введем коэффициенты и правые части новой системы уравнений. В диапазоне F 17: F 20 автоматически отобразится решение новой системы уравнений. Проверить правильность алгоритма можно, например, заменив числа в столбце E 1: E 4 суммами коэффициентов уравнений. Тогда вектор решений должен состоять из единиц. Приведем программу на языке C ++ для решения системы линейных уравнений методом Гаусса с выбором главного элемента:
#include <except.h> #include <iostream.h> int gauss(long double **a, long double *b, long double *x, const int n); int main(){ long double **a; long double *b; long double *x; int i,j,n; cout <<" input n = "; cin >> n; try { a= new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n]; b= new long double[n]; x= new long double[n]; } catch (xalloc){cout <<"\nCould not allocate\n"; exit(-1);} cout <<"\n input matrix a \n"; for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j]; cout <<"\n input vector b\n"; for (i=0; i<n; i++)cin >> b[i]; cout << "\n matrix a: "; for (i=0; i<n; i++){cout << "\n"; for (j=0; j<n; j++) cout <<" "<< a[i][j];} cout << "\n vector b: "; for (i=0; i<n; i++)cout << "\n " << b[i]; gauss(a, b, x, n); cout << "\n vector x: "; for (i=0; i<n; i++)cout << "\n x[" << i <<"] = " << x[i]; cout << "\n Press Key and Enter to continue"; cin >> i; // for pause for(i=0;i<n;i++)delete[] a[i]; delete a; delete[] b; delete[] x; return 0; }//end main int gauss(long double **a, long double *b, long double *x, const int n){ // Метод Гаусса с выбором главного элемента int i, k, m, im; long double amm, aim, r; for (m = 0; m <= n-2; m++) {// m amm = a[m][m]; im = m; for (i = m; i <= n-1; i++) if(a[i][m] > amm){amm = a[i][m]; im = i; } if(im!= m){r = b[im]; b[im] = b[m]; b[m] = r; for (k = m; k <= n-1; k++) {r = a[im][k]; a[im][k] = a[m][k]; a[m][k] = r;} } for (k = m; k <= n-1; k++)a[m][k] = a[m][k]/amm; // 3.16 b[m] = b[m] / amm; // for (i = m + 1; i <= n-1; i++){// i aim = a[i][m]; for (k = m; k <= n-1; k++) a[i][k] = a[i][k] - a[m][k]*aim; // 3.17 b[i] = b[i] - b[m]*aim; // }// end i }// end m x[n-1] = b[n-1]/a[n-1][n-1]; // 3.19 for (i = n - 2; i >= 0; i--){// i x[i] = b[i]; // for (k = i + 1; k < n; k++) // 3.20 x[i] = x[i] - a[i][k]*x[k]; // }// end i return 0; }// end gauss
Приведем для сравнения вариант процедуры обычного метода Гаусса:
int gauss(long double **a, long double *b, long double *x, const int n){ // Метод Гаусса int i, k, m; long double amm, aim; for (m = 0; m <= n-2; m++) {// m amm = a[m][m]; for (k = m; k <= n-1; k++)a[m][k] = a[m][k]/amm; // 3.16 b[m] = b[m] / amm; for (i = m + 1; i <= n-1; i++){// i aim = a[i][m]; for (k = m; k <= n-1; k++) a[i][k] = a[i][k] - a[m][k]*aim; // 3.17 b[i] = b[i] - b[m]*aim; } // end i } // end m x[n-1] = b[n-1]/a[n-1][n-1]; // 3.19 for (i = n - 2; i >= 0; i--){// i x[i] = b[i]; for (k = i + 1; k < n; k++) // 3.20 x[i] = x[i] - a[i][k]*x[k]; } // end i return 0; } // end gauss
Отметим, что в процедуре gauss() массивы исходных данных a и b не сохраняются, так как результаты преобразований записываются в эти же массивы.
|
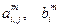, причем 
.
:
; 
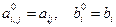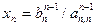