Векторное пространствоКонтрольные вопросы: 1. Линейное пространство. Векторное пространство. 2. Свойства линейных операций над векторами. 3. Скалярное произведение двух векторов. Некоторые приложения скалярного произведения. 4. Евклидово пространство. 5. Векторное произведение двух векторов. Некоторые приложения векторного произведения. 6. Смешанное произведение трех векторов. 7. Собственные значения и собственные векторы матрицы. 1. Линейное пространство. Векторное пространство. Совокупность векторов одной размерности называют системой векторов и обозначают:
Система ненулевых векторов (1) называется линейно зависимой, если существуют такие числа
Если равенство (2) для данной системы векторов (1) возможно лишь при Максимально независимой подсистемой системы векторов (1) называется частичный набор векторов этой системы, удовлетворяющий условиям: 1) векторы этого набора независимы; 2) любой вектор системы (1) линейно выражается через векторы этого набора. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным ниже восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством. 2. Линейные операции над любыми векторами удовлетворяют следующим свойствам: 1°. х+у=у+х – коммутативное (переместительное) свойство сложения. 2°. (х+у)+z=x+(y+z) – ассоциативное (сочетательное) свойство сложения. 3°. α(β х)=(αβ) х – ассоциативное свойство относительно числового множителя. 4°. α (х+у)= α х +α у – дистрибутивное (распределительное) свойство относительно суммы векторов. 5°. (α+β) х =α х +β х – дистрибутивное свойство относительно суммы числовых множителей. 6°. Существует нулевой вектор 0 =(0;0;…0) такой, что х+0=х для любого вектора х. 7°. Для любого вектора х существует противоположный вектор (-х) такой, что х+(-х)=0. 8°. Отметим, что под х, у, z можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае множество элементов называется линейным пространством. 3. Скалярным произведением двух векторов
где φ; – угол между векторами Некоторые приложения скалярного произведения. 1.Угол между векторами. Определение угла
Отсюда следует условие перпендикулярности ненулевых векторов
2.Работа постоянной силы. Пусть материальная точка перемещается прямолинейно из положения
Рис. 2 Из курса физики известно, что работа силы Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения. 4. Евклидово пространство. Скалярное произведение имеет следующие свойства: 1°. ху=ух – коммутативное свойство. 2°. х(у+z)=xy+xz – дистрибутивное свойство. 3°. ( α х)у =α (ху) – для любого действительного числа α. 4°. хх >0, если х – ненулевой вектор, хх =0, если х – нулевой вектор. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством. 5. Векторным произведением двух векторов
Геометрически
Рис. 3 Условие коллинеарности векторов: Если
Некоторые приложения векторного произведения. 1.Определение момента силы относительно точки. Пусть в точке Из курса физики известно, что моментом силы 1) перпендикулярен плоскости, проходящей через точки 2) численно равен произведению силы на плечо
3) образует правую тройку с векторами Значит,
Рис.4 2.Нахождение линейной скорости вращения. Скорость
Рис.5 6. Смешанным произведением трех векторов
Модуль смешанного произведения равен объему параллелепипеда, построенного на векторах Условие компланарности векторов. Векторы
7. Вектор-столбец
называется собственным вектором квадратной матрицы А n -го порядка, соответствующим собственному значению λ, если он удовлетворяет матричному уравнению Здесь Е – единичная матрица n -го порядка, 0 – нулевой вектор-столбец. При условии, что вектор
Координаты собственного вектора
Собственный вектор определяется до постоянного множителя.
З а д а н и е 1. Написать разложение вектора Р е ш е н и е. Запишем вектор
Подставим координаты заданных векторов. Получим систему
решив которую, найдем коэффициенты З а д а н и е 2. Найти угол между векторами Р е ш е н и е. Воспользуемся формулой Найдем скалярное произведение векторов З а д а н и е 3. Найти проекцию вектора Р е ш е н и е. Проекция вектора З а д а н и е 4. Вычислить площадь параллелограмма, построенного на векторах Р е ш е н и е.
Вычислим модуль полученного векторного произведения, который и будет численно равен искомой площади параллелограмма: З а д а н и е 5. Параллелограмм построен на векторах Р е ш е н и е.
Следовательно,
З а д а н и е 6. Компланарны ли векторы Р е ш е н и е. Если векторы компланарны, то их смешанное произведение равно нулю. Проверим это. Найдем смешанное произведение данных векторов:
З а д а н и е 7. Точки Р е ш е н и е. Объем пирамиды будем Найдем координаты этих векторов, а затем их смешанное произведение.
Теперь найдем площадь грани
Т.к. З а д а н и е 8. Найти вектор Р е ш е н и е. Пусть вектор
Решив полученную систему, получим, что З а д а н и е 9. Зная векторы Р е ш е н и е. Угол при вершине
|

 (1)
(1)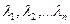 , не равные нулю одновременно, что линейная комбинация данной системы с указанными числами равна нулевому вектору:
, не равные нулю одновременно, что линейная комбинация данной системы с указанными числами равна нулевому вектору: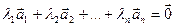 (2)
(2)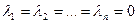 , то такая система векторов называется линейно независимой.
, то такая система векторов называется линейно независимой.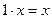 для любого вектора х.
для любого вектора х. и
и 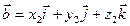 называется число, определяемое равенством
называется число, определяемое равенством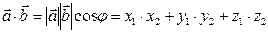 (3)
(3) и
и 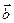 .
.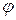 между ненулевыми векторами
между ненулевыми векторами 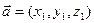 и
и 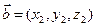 :
: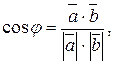 т.е.
т.е. 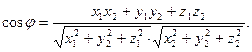
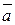 и
и 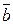 :
: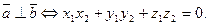
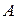 в положение
в положение 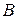 под действием постоянной силы
под действием постоянной силы 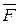 , образующей угол
, образующей угол  (рис. 2).
(рис. 2).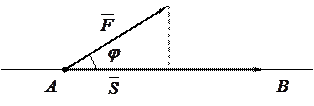
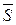 равна
равна 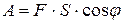 , т.е.
, т.е.  .
. , длина которого равна произведению длин векторов
, длина которого равна произведению длин векторов  (4)
(4)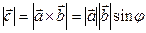
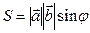
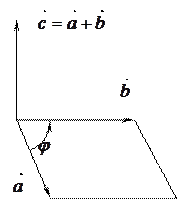
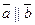 , то
, то  (и наоборот), т. е.
(и наоборот), т. е.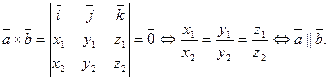
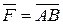 и пусть
и пусть 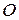 - некоторая точка пространства (рис. 4).
- некоторая точка пространства (рис. 4).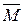 , который проходит через точку
, который проходит через точку 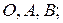
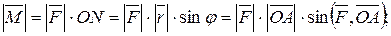
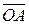 и
и 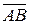 .
.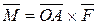 .
.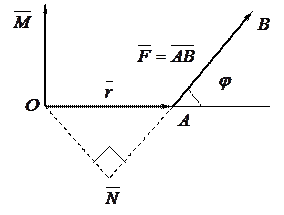
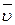 точки
точки 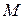 твердого тела, вращающегося с угловой скоростью
твердого тела, вращающегося с угловой скоростью 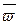 вокруг неподвижной оси, определяется формулой Эйлера
вокруг неподвижной оси, определяется формулой Эйлера 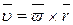 , где
, где 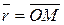 , где
, где 
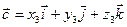 называется число, равное
называется число, равное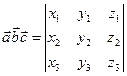 (5)
(5)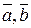 и
и 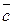 компланарны тогда и только тогда, когда их смешанное произведение равно нулю при условии, что
компланарны тогда и только тогда, когда их смешанное произведение равно нулю при условии, что 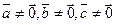 :
: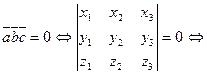 векторы
векторы 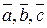 компланарны.
компланарны.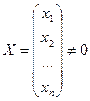
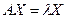 или
или  .
.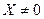 , получаем характеристическое уравнение для определения собственных значений λ:
, получаем характеристическое уравнение для определения собственных значений λ: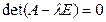 (6)
(6)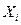 , соответствующего собственному значению
, соответствующего собственному значению 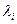 , являются решением системы уравнений:
, являются решением системы уравнений: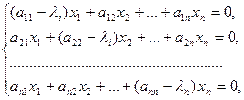 (7)
(7) по векторам
по векторам 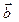 ,
, 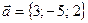 ,
, 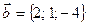 ,
, 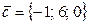 ,
, 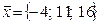 .
.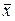 в виде линейной комбинации векторов
в виде линейной комбинации векторов 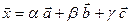 . Найдем коэффициенты
. Найдем коэффициенты 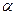 ,
, 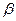 ,
, 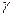 . Для этого запишем разложение вектора
. Для этого запишем разложение вектора 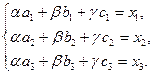
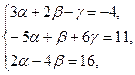
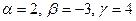 . Т.е.
. Т.е. 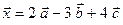 .
. и
и 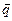 , если
, если 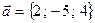 ,
, 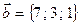 ,
, 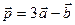 ,
, 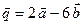 .
.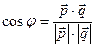 . Определим координаты векторов
. Определим координаты векторов 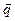 , при этом учтем, что при умножении вектора на число, мы умножаем на это число каждую координату этого вектора, а при сложении векторов – складываем одноименные координаты:
, при этом учтем, что при умножении вектора на число, мы умножаем на это число каждую координату этого вектора, а при сложении векторов – складываем одноименные координаты: 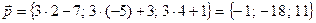 ,
, 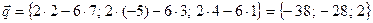 .
.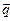 и их длины.
и их длины. 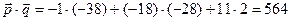 ,
,  ,
, 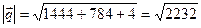 . Подставив в формулу, получим
. Подставив в формулу, получим 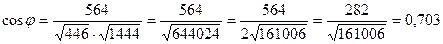 . Отсюда
. Отсюда 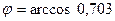 .
. на вектор
на вектор  , если
, если 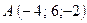 ,
, 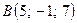 ,
, 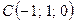 .
. . Определим координаты векторов
. Определим координаты векторов 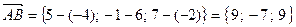 ,
, 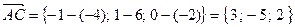 ,
, 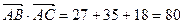 ,
, 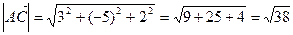 . Тогда
. Тогда 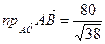 .
.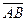 и
и 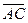 , если
, если 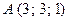 ,
, 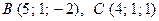 .
.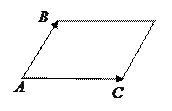 Площадь параллелограмма будем искать по формуле
Площадь параллелограмма будем искать по формуле 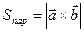 . Для этого найдем сначала координаты векторов
. Для этого найдем сначала координаты векторов 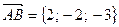 ,
,  ,
,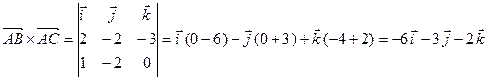 .
.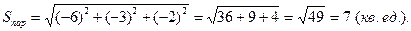
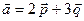 и
и 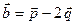 , где
, где  ,
, 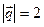 ,
, 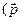 ^
^  . Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
. Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.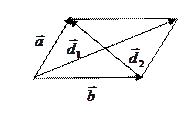
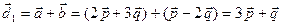 ,
, 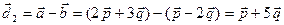 ,
,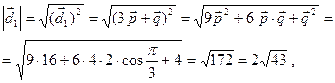
 Угол между диагоналями обозначим буквой
Угол между диагоналями обозначим буквой 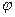 , тогда
, тогда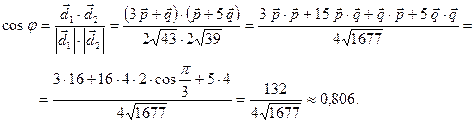
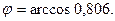
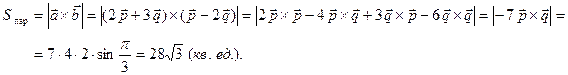
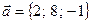 ,
, 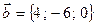 ,
, 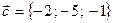 ?
?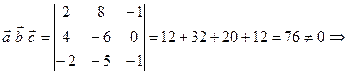 векторы некомпланарны.
векторы некомпланарны.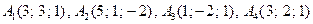 являются вершинами пирамиды. Вычислить ее объем, площадь грани
являются вершинами пирамиды. Вычислить ее объем, площадь грани  и высоту пирамиды, опущенную на эту грань.
и высоту пирамиды, опущенную на эту грань.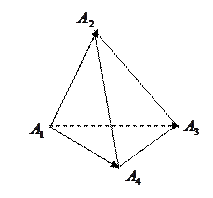 искать по формуле
искать по формуле 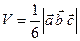 , где
, где  .
.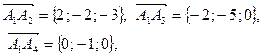
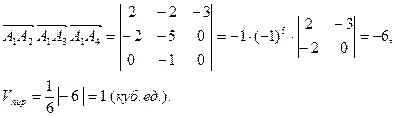
 .
.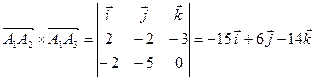 . Тогда площадь грани будет равна
. Тогда площадь грани будет равна 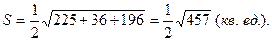
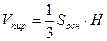 , то высота H =
, то высота H = 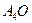 , опущенная на грань
, опущенная на грань 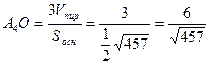 .
.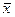 , перпендикулярный к векторам
, перпендикулярный к векторам 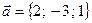 и
и  и удовлетворяющий условию
и удовлетворяющий условию 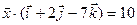 .
. имеет координаты
имеет координаты 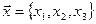 . Т. к. вектор
. Т. к. вектор  . Запишем все три скалярных произведения в координатной форме:
. Запишем все три скалярных произведения в координатной форме: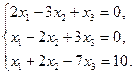
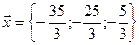 .
.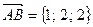 и
и 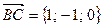 , совпадающие с двумя сторонами треугольника, найти угол при вершине
, совпадающие с двумя сторонами треугольника, найти угол при вершине 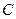 и площадь треугольника.
и площадь треугольника.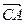 и
и 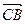 . Вектор
. Вектор 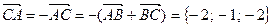 , тогда
, тогда  ,
,


