Работа по перемещению проводника с током в магнитном поле.Проводник длиной l (он может свободно перемещаться) с током I находится в однородном магнитном поле (см. рисунок). Поле направлено перпендикулярно плоскости рисунка — из-за чертежа. Сила Ампера F = IBl. Под ее действием проводник переместился из положения 1 в положение 2. Работа, совершаемая магнитным полем: dA = Fdx = I dx [ l, B ] = IBldx = IBdS = Id Φ. Использованы соотношения: dS = ldx — площадь, пересекаемая проводником при его перемещении в магнитном поле; BdS = d Φ — поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом, dA = Id Φ. Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
Вопрос 25. Циркуляция и ротор вектора индукции магнитного поля. Теорема Гаусса для магнитного поля. Вывод выражения для циркуляции вектора В
При этом ток Ii в сумме считается положительным, если его направление связано с направлением обхода контура правилом «правого винта».
интегрирование по α в пределах [0; 2π] дает выражение для циркуляции что и требовалось доказать.
Ротор вектора В
Из (11) видно, что rot B совпадает по направлению с вектором плотности тока j.
Такое векторное поле принято называть вихревым (или соленоидальным) полем. Теорема Гаусса для магнитного поля в интегральной и дифференциальной формах Интегральная форма
Эта теорема является фундаментальным законом для магнитного поля (она выполняется для любых магнитных полей) и выражает собой в постулативной форме тот экспериментальный факт, что линии вектора В не имеют ни начала, ни конца – они замкнуты сами на себе (где-то, вообще говоря, на бесконечности). Иначе можно трактовать теорему Гаусса для В, как отсутствие в природе «магнитных зарядов» (т.е. зарядов, имеющих значение как электрические заряды).
Число линий В, входящих в объем V, ограниченный замкнутой поверхностью S, равно числу линий В, выходящих из этого объема. Следствием из этого является того, что магнитный поток не зависит от формы поверхности и определяется только ее размером S. Иначе говоря, магнитный поток не зависит от формы поверхности, «натянутой» на контур Г. Дифференциальная форма
Дивергенция вектора индукции магнитного поля всюду равна нулю, т.е. магнитное поле не имеет источников и является вихревым (или соленоидальным) полем. Вопрос 26. Расчет магнитных полей соленоида и тороида с использованием теоремы о циркуляции вектора H.
Магнитное поле соленоида
Пусть на единицу длины соленоида приходится п -витков провода с током I. Если шаг винтовой линии достаточно мал, то каждый виток можно приблизительно считать замкнутым витком с током I (как круговой ток). Будем также считать, что сечение провода очень мало, и ток в соленоиде течет по его наружной поверхности, т. е. по каркасу катушки Dк. Опыт показывает, что чем длиннее соленоид (Lк >> Dк), тем меньше индукция магнитного поля снаружи. В пределе – для бесконечно длинного соленоида – снаружи В = 0 и все поле сосредоточено внутри соленоида; причем силовые линии В внутри расположены равномерно и параллельно оси соленоида, т. е. поле в соленоиде однородно В = const при I = const. Поэтому, если выбрать контур в виде прямоугольника (см рис.) со стороной l, охватывающий ток (n∙I∙l), то циркуляция В в этом случае будет: B∙l = μ0∙n∙I∙l. Отсюда получаем искомую индукцию в соленоиде: B = μ0∙n∙I (12) Магнитное поле тороида Тороид представляет собой магнитную систему в форме катушки с проводом, плотно навитым на тороидальный каркас круглого сечения. Пусть Rср – средний радиус тора, N – число витков в обмотке тороида, I – ток в обмотке тогда из соображений симметрии следует, что линии магнитной индукции В здесь будут представлять собой окружности с центрами на оси ОО' тороида. Поэтому в качестве контура интегрирования следует выбрать одну из этих окружностей (с радиусом r).
Для реального тороида, у которого витки не параллельны оси ОО', образуется наряду с азимутальным еще и полоидальное поле. Вопрос 27. Намагниченность вещества. Циркуляция вектора намагниченности. Магнитная восприимчивость и магнитная проницаемость. Связь векторов магнитного поля: B, J, H. Намагниченность вещества. Всякое вещество является магнетиком, т.е. способно под действием внешнего магнитного поля намагничиваться – приобретать магнитный момент. Намагниченное вещество создает свое магнитное поле В’, которое вместе с исходным полем В0, обусловленным токами проводимости, образует результирующее поле (в пространстве, занятом магнетиком): В = В0 + B’ (1)
Под действием внешнего поля В0 магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вещество – намагничивается, т.е. и образуется поле B’.
Вектор намагниченности можно также представить как: J=n. < pmi >, где n – концентрация молекул, < pmi > - средний магнитный момент одной молекулы.
т.е. силовые линии В всегда замкнуты. Намагничивание вещества также связано с преимущественной ориентацией (а для ряда магнетиков – индуцированием) молекулярных токов, которые могут образовывать, так называемые, макроскопические токи намагничивания I’. Обычные токи, текущие по проводникам и связанные с дрейфом в веществе носителей тока, называют токами проводимости I. Рассмотрим некоторый цилиндр из однородного магнетика, намагниченность J которого однородна и направлена вдоль оси. Молекулярные токи в магнетике ориентированы как показано на рисунке. Причем у соседних молекул токи в местах их соприкосновения взаимно компенсируются. Неском-пенсированными остаются только токи, которые выходят на боковую поверхность цилиндра. Эти токи образуют макроскопический поверхностный ток намагничивания I‘пов, который для длинного магнетика определяют через линейную плотность тока i’ [А/м]: I‘пов = i’.l
В неоднородном магнетике под действием внешнего магнитного поля молекулярные токи «выстраиваются» аналогичным образом, но так как их величина различна (на рисунке эти токи растут вдоль оси х), то полной взаимной компенсации этих токов в объеме магнетика – не происходит и образуется (наряду с поверхностным током I’пов) макроскопический объемный ток намагничивания I’об , который течет вдоль оси y и может быть определен через поверхностную плотность тока j’ [А/м2]: I’об = j’.∆S, где ∆S – сечение магнетика в плоскости zx.
Докажем следующую теорему: т.е. циркуляция намагниченности J по произвольному замкнутому контуру Γ равна алгебраической сумме токов намагничивания I’, охватываемых данным контуром. Вычислим алгебраическую сумму молекулярных токов, охватываемых контуром Γ; причем, как видно из рисунка, только те молекулярные токи, которые обвиваются вокруг контура и пересекают натянутую поверхность S один раз, учитываются в этой сумме. Если каждый молекулярный ток равен Iм , а площадь его контура Sм, то, как видно из следующего рисунка, элемент dl контура Γ обвивают те молекулярные токи, центры которых попадают внутрь косого цилиндра с объемом dV=Sм.cosα.dl, где α - угол между dl и намагниченностью J в данном месте. Эти токи пересекают поверхность S один раз, и их вклад в общий ток I’ составляет: dI’=Iм.n.dV, где n – концентрация молекул магнетика.
Ротор намагниченности равен плотности тока намагничивания в той же точке вещества. Циркуляция вектора магнитной индукции в веществе.
где I – ток проводимости и I´; - ток намагничивания, охватываемые заданным контуром Г.
получаем после деления на μ0 уравнение (5) в виде: Величину, стоящую под интегралом в скобках, называют напряженностью магнитного поля.
Ротор вектора Н равен плотности тока проводимости в той же точке вещества.
где χ– магнитная восприимчивость вещества (величина безразмерная, характеризует магнитные свойства вещества). Связь между векторами В и H
или представлено в виде
Так как для вакуума имеем В 0 = μ0 . Н 0, то вследствие (10) магнитная проницаемость μ показывает, во сколько раз магнитное поле токов проводимости усиливается за счет намагничения среды. Вопрос 28. Магнитное поле в веществе. Диамагнетики, парамагнетики, ферромагнетики и особенности в их намагниченности. Если несущие ток провода находятся в какой-либо среде, магнитное поле изменяется. Это объясняется тем, что всякое вещ0во является магнетиком Диамагне́тики — вещества, намагничивающиеся против направления внешнего магнитного поля. В отсутствие внешнего магнитного поля диамагнетики немагнитны. Под действием внешнего магнитного поля каждый атом диамагнетика приобретает магнитный момент I,пропорциональный напряжённости поля Н и направленный навстречу полю. Поэтому магнитная восприимчивость χ = I/H у диамагнетиков всегда отрицательна. По абсолютной величине диамагнитная восприимчивость χ мала и слабо зависит как от напряжённости магнитного поля, так и от температуры. Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначительно отличается от единицы μ>1. Ферромагнетики (железо) - способны обладать намагниченностью в отсутствии внешнего магнитного поля.
Вопрос 29. Поле на границе раздела двух однородных магнетиков. Условия преломления для векторов B и H.
2) теоремы о циркуляции Н, т. е. Условие для В Представим очень малой высоты цилиндр, расположенный на границе раздела магнетиков. Поток вектора В наружу из этого цилиндра определяется через его торцы (потоком через боковую поверхность пренебрегаем ввиду малости высоты): В 2n. ΔS + B 1n´. ΔS = 0. Взяв обе проекции В на общую нормаль n с учетом В 1n´=- B 1n получаем В 2n = B 1n, т. е. нормальная составляющая вектора В разрыва не претерпевает на границе раздела сред. В то же время с учетом μ2.μ0. Н 2n= μ1.μ0. Н 1n получаем, т. е. нормальная составляющая вектора Н претерпевает разрыв.
Условия для Н Для общности будем предполагать, что вдоль поверхности раздела магнетиков течет поверхностный ток проводимости с линейной плотностью i [А/м]. Применим теорему о циркуляции вектора Н к малому прямоугольному контуру, высота которого пренебрежимо мала по сравнению с длиной l (последняя также достаточно мала). Таким образом, имеем уравнение: H 2τ. l + H 1τ´. l = in.l, где in – проекция вектора тока проводимости i на нормаль n к контуру. После замены H 1τ´ на - H 1τ и сокра-щения на l получаем:
Преломление силовых линий на границе раздела магнетиков
Для случая отсутствия токов проводимости, как видно из рис. 1, имеем так как В 2n = B 1n. При переходе в более «магнитоплотную» (μ2 > μ1) среду происходит увеличение густоты линий В (т.е. В 2 > В 1), а линии Н терпят разрыв из-за поверхностных токов намагничивания и, следовательно, Н 2 < Н 1 (см. рис. 2). Замечание: На особенностях преломления силовых линий основана магнитная защита с помощью замкнутой железной оболочки (рис. 3), в которой магнитное поле будет концентрироваться, а в полости оболочки поле будет сильно ослаблено по сравнению с внешним. Билет 30. Закон Фарадея для электромагнитной индукции. Правило Ленца. Индуктивность контура. Расчет индуктивности соленоида. Открытие Фарадея В 1831 г. Майкл Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного потока (т. е. потока вектора В: Ф = В .S), охватываемого этим контуром, возникает электрический ток – последний назвали индукционным током (Ii). Само это явление было названо электромагнитной индукцией. Появление индукционного тока означало, что при изменении магнитного потока – в контуре возникает э.д.с. индукции Ei. При этом было отмечено, что величина э.д.с. совершенно не зависит от того, каким образом произошло изменение потока Ф, и определяется лишь скоростью его изменения, т. е. величиной d Ф /dt, и, соответственно, закон Фарадея получил аналитическое выражение:
Ei = Фарадей обнаружил, что индукционный ток (см. рис.) можно вызвать двумя различными способами: 1) перемещением рамки Р (или ее отдельных частей – деформация рамки) в постоянном магнитном поле В неподвижной катушки К; 2) изменением магнитного поля В (за счет движения катушки К, или вследствие изменения тока I в ней, или в результате того и другого вместе) при неподвижной рамки Р.
Правило Э.Х. Ленца Правило устанавливает направление индукцион-ного тока (а, следователь-но, и знак Ei). Оно гласит: индукционный ток всегда направлен так, чтобы про-тиводействовать причине, его вызывающей. Физическая природа электромагнитной индукции Рассмотрим контур с подвижной перемычкой длины l, который находится в однородном постоянном магнитном поле В, перпендикулярном плоскости контура и направленном за плоскость рисунка. Начнем двигать перемычку вправо со скоростью v; с этой же скоростью будут двигаться и носители тока в перемычке – электроны. Тогда на каждый электрон начнет действовать вдоль перемычки магнитная сила Лоренца, направленная вниз: Fл = -e. (v x B). Произойдет перераспре-деление носителей в перемычке (внизу накопятся электроны, а вверху образуется избыток положительных ионов); в контуре появится ток – индукционный ток, направленный «вверх» - против часовой стрелки. И, если движение перемычки со скоростью v будет продолжаться, то и индукционный ток будетподдерживаться в контуре. Следовательно, сила Fл здесь играет роль сторонней силы, и ей соответствует поле сторонних сил: E* = = F л /-e =(v x B), где (v x B) постоянный вектор. Так как циркуляция вектора Е* определяет э.д.с. в
контуре, то здесь имеем Ei =
Ei =, где (l x v . dt) = - n . dS. В результате получаем доказываемое выражение
Ei = Это также объясняется с позиций закона Фарадея… Элект-рический ток, текущий в любом контуре, создает пронизывающий этот же контур магнитный поток Ф = В . S, который, как видно из экспериментов, будет пропорционален самому току, т. е. Ф = L . I где L – коэффициент пропорциональности, называемый индуктивностью контура. Расчет индуктивности реальных контуров Расчет индуктивности длинного соленоида с сердечником (μ;). 1) Определяем индукцию магнитного поля в соленоиде: В = μ.μ0.Н, где напряженность поля соленоида Н = n.I =N/l.I (N – полное число витков, l - длина соленоида). Таким образом, В = μ.μ0. (N/l). I; 2) Определяем потокосцепление с соленоидом: Ψ = N. (μ.μ0.N/l.I). S, а с учетом, что объем соленоида V=S.l, получаем Ψ = μ.μ0.N 2 /l 2. V.I = μ.μ0.n 2. V.I; 3) Рассчитываем индуктивность: L = Ψ/I = μ.μ0.n 2. V.
Билет 31. Явление самоиндукции и взаимной индукции. Вихревые токи. Самоиндукция Это явление возникновения ЭДС индукции в проводящем контуре при изменении тока, протекающего через контур.Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L:
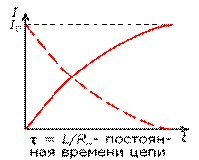
Характерные процессы самоиндукции наблюдаются при замыкании и размыкании электрических цепей, содержащих индуктивность L и сопротивление Rн. Так установление тока в реальных цепях происходит после соответствующей коммутации – не мгновенно, а за определенный промежуток времени (см. график).
ВЗАИМНАЯ ИНДУКЦИЯ Рассмотрим два неподвижных контура 1 и 2, расположенных достаточно близко друг от друга. Если в контуре 1 течет ток I1, то он создает через контур 2 полный магнитный поток (в случае отсутствия ферромагнетиков) Ф2= L21.I1 . При изменении тока I1 во времени в контуре 2 наводится э.д.с. индукции: Ei2 = - L21.dI1/dt (4) Аналогично, при протекании тока I2 в контуре 2 возникает сцепленный с контуром 1 магнитный поток Ф1 = L12.I2, а при изменениях тока I2 в контуре 1 индуцируется э.д.с.: Ei1 = - L12.dI2/dt (5) Контуры 1 и 2 в этом случае называются связанными. Явление возникновения э.д.с. в одном из связанных контуров при изменениях силы тока в другом контуре называется взаимной индукцией. Коэффициенты пропорциональности L12 и L21 называются взаимной индуктивностью контуров. Соответствующий расчет дает, что в отсутствии ферромаг-нетиков эти коэффициенты всегда равны: L12 = L21.
Замечание: В отличие от собственной индуктивности контура L, которая всегда положительная величина, взаимная индуктивность L12 – величина алгебраическая (в частности, может равняться нулю). Это связано с тем, что поток Ф1 и ток I2 относятся к разным контурам и их знаки зависят от выбора нормали n 1 к контуру 1 и направления обхода контура 2, которые в свою очередь должны вместе с обходом контура 1 и нормалью к контуру 2 – образовывать правовинтовые системы. Вихревые токи (или токи Фуко) – это индукционные токи, которые возбуждаются в сплошных массивных проводника. Электросопротивление массивного проводника – мало, поэтому токи Фуко могут достигать очень больших величин. В соответствии с правилом Ленца токи Фуко выбирают внутри проводника такие направления, чтобы своим действием возможно сильнее противиться причине, которая их вызывает.
Билет 32. Энергия тока в контуре, обладающем индуктивностью L.Энергия магнитного поля. Объемная плотность этой энергии. Рассмотрим электрическую цепь, содержащую индуктив-ность L и сопротивление R, которую с помощью быстро-действующего коммутатора Кл подключим (из а в б) к источнику питания E. В таком замкнутом контуре начнет возрастать ток, а это приведет к появлению э.д.с. самоиндукции ES. Тогда согласно закону Ома имеем R.I = E + ES или E = R.I – ES. Найдем элементарную работу δАстор, которую совершают сторонние силы источ-ника E за время dt, для этого умножим последнее уравнение на (I.dt): E.I.dt = R.I 2. dt – ES.I.dt (6)C учетом смысла каждого слагаемого в уравнении (6) и закона Фарадея ES= -dФ/dt, представим (6) как δАстор= δQ + I.dФ, где δQ – джоулево тепловыделение, а слагаемое I.dФ (так называемая дополнительная работа δАдоп) опреде-ляет работу источника против э.д.с. самоиндукции. Далее будем считать, что вблизи контура нет ферромагнетиков, следовательно, dФ = L.dI и получаем δАдоп= I.dФ = L.I.dI.
Проинтегрировав последнее выражение, получаем: Адоп= ∫δАдоп= (L.I 2)/2 (7) Таким образом, часть работы источника питания (Адоп) идет на «создание» магнитного поля, т.е. превращается в энергию магнитного поля, обусловленного протеканием тока в катушке с индуктивностью L. Иначе говоря, в отсутствии ферромагне-тиков контур с L, по которому течет ток I, обладает энергией: W = (L.I 2)/2 = (I.Ф)/2 = Ф 2/(2 L) (8) Эту энергию называют магнитной энергией тока или собственной энергией контура с током. Она может быть целиком превращена во внутреннюю энергию проводников (нагрев RH), если отключить источник E, быстро повернув ключ Кл в положение а. Для длинного соленоида: индуктивность L = μμ;0 n 2 V, где n – число витков на единицу длины, V – объем соленоида; имеем W = (L.I 2)/2 = μμ;0 n 2. I 2. V /2, а с учетом, что n.I = H = B /(μμ;0), получаем W = μμ;0 H2 /2. V = B 2/(2 μμ;0). V = (B . H)/2. V. Выражения w = μμ;0 H 2/2 = B 2/(2 μμ;0) = (B . H)/2 (9) определяют объемную плотность энергии магнитного поля. Зная плотность энергии магнитного поля в каждой точке, можно определить энергию поля, заключенную в любом объеме V: W = ∫;(B . H)/2. dV (10) Замечание: Часто приходится использовать «энергетический» метод при нахождении индуктивности контура (когда вычисление магнитного потока через контур затруднительно), т. е. L = 1/ I 2. ∫B 2/(μμ;0). dV (11)
(12) где Lik= Lki – взаимная индуктивность i- го и k- го контуров, Lii=Li – собственная индуктивность i- го контура. Наиболее общим методом определения сил в магнитном поле является энергетический, при этом используют выражение (12) для энергии магнитного поля. Для случая двух контуров с токами I1 и I2 магнитную энергию можно представить как: W = 1/2(I1.Ф1 + I2.Ф2) (13) где Ф1= L1.I1 + L12.I2, Ф2= L2.I2 + L21.I1 – полные магнитные потоки через контура 1 и 2 соответственно. Согласно закону сохранения энергии элементарная работа δА*, которую совершают источники тока, включенные в эти контура, идет: на теплоту δQ, на приращение магнитной энергии системы dW (в ходе движения контуров или при изменении токов в них), на механическую работу δАмех (при перемещении или деформации контуров), т. е. δА*= δQ + dW + δАмех Нас интересует только работа источников против э.д.с. индукции и самоиндукции в каждом контуре, т. е. дополни-тельная работа: δАдоп= - (Ei1 + ES1). I1.dt – (Ei2 + ES2). I2.dt, а с учетом, что (Ei + ES) = - dФ/dt, получаем δАдоп= I1.dФ1 + I2.dФ2. Именно дополнительная работа источников идет на приращение магнитной энергии и на механическую работу, таким образом имеем: I1.dФ1 + I2.dФ2 = dW + δAмех (14) Формула (14) является основной для расчета δАмех, а затем и сил в магнитном поле, используя определение работы δА= F.dl. В итоге сила в магнитном поле определяется производными: F = - dWФ / dl = dWI / dl (15) где dWФ - приращение магнитной энергии в случае Ф1;2= const, а dWI - приращение магнитной энергии в случае I1;2= const. Замечание: Так из формулы (13) для случая постоянных токов в контурах: dWI = ½(I1.dФ1 + I2.dФ2). Вопрос 33. Обобщение максвеллом закона электромагнитной индукции. Понятие Вихревого электрического поля. Циркуляция вектора Е. Обобщение Дж. Максвеллом закона электромагнитной индукции Как экспериментально установлено М. Фарадеем (в 1831 г.) любое изменение магнитного потока, пронизывающего замкнутый проводящий контур, приводит к возникновению в нем э.д.с. индукции и появлению индукционного тока, т.е.
Ei = (1)
Согласно определению э.д.с. Ei =, поэтому закон (1) можно записать в виде, где дифференцирование по t
(2) Здесь индукция В, вообще говоря, зависит как от времени, так и от координат, поэтому используется частная производная
Уравнение (3) также подчеркивает вихревой характер поля Е В в виду наличия ротора.
(наличие) обуславливает появление в пространстве вихревого электрического поля Е В независимо от присутствия проволочного контура, наличие которого лишь позволяет обнаружить это поле по индикации индукционного тока.
ротор, а дивергенция
Уравнения (4) определяют взаимосвязь между электрическим и магнитным полями, которая в свою очередь служит причиной того, что раздельное рассмотрение этих полей имеет лишь относительный смысл – относительно выбранной инерциальной системы отсчета, где соответст-вующие им электрические заряды неподвижны, а электри-ческие токи стационарны. Относительно других движущихся систем отсчета следует уже рассматривать совокупность электрического и магнитного полей, образующих единое электромагнитное поле. Вопрос 34. Циркуляция вектора Н с позиции Максвелла. Ток смещения. Закон полного тока.
Циркуляция вектора Н с позиции максвелла.
где I – ток в проводниках. Применим эту теорему для случая разрядки предварительно заряженного конденсатора, где в качестве контура интегрирования Г выберем замкнутую кривую, охватывающую провод с током разрядки I.
На контур Г можно «натянуть» две поверхности S1 и S2, которые имеют «равные права» в соответствии с теоремой о циркуляции. Однако через поверхность S1 течет ток I и, следовательно, выполняется равенство (5), а через поверх-ность S2 не течет никакого тока и циркуляция Н равна 0, т.е. циркуляция зависит от выбора поверхности, которую мы «натягиваем» на контур Г. Это противоречит теореме о циркуляции для случая постоянных полей (постоянного тока), но в данном случае ток разрядки сугубо переменный:
(или).
Сложив отдельно левые и правые части уравнений (7) и (8), получаем (9)
Согласно уравнению (9) линии полного тока j пол являются непрерывными, т.е. токи проводимости j, если они не замкнуты (как в случае конденсатора), замыкаются токами смещения j см.
Это уравнение также будем называть 2-ым уравнением Максвелла (в интегральной форме).
Т.е. ротор вектора Н определяется плотностью тока проводимости j и плотностью тока смещения в той же точке пространства, в котором действует электромагнитное поле. О физической сущности тока смещения
Вопрос 35. Системы уравнений Максвелла в интегральных и дифференциальных формах. Основу макроскопической единой электромагнитной теории образуют фундаментальные уравнения электродинамики неподвижных сред (или коротко – уравнения Максвелла). Эти уравнения нельзя «вывести» из каких-либо законов, положений; они являются основными аксиомами, постулатами электродинамики, полученными путем обобщения огромного количества экспериментальных фактов.
Дополнительными уравнениями к системе основных уравнений Максвелла являются материальные уравнения, определяющие индивидуальные свойства среды, в которой существует электромагнитное поле. D = ε.ε0. E; B = μ.μ0. H; j = σ(E + E *) (12) где ε и μ – диэлектрическая и магнитная проницаемости, а σ– электропроводность среды; Е *- поле сторонних сил (не э/м). Рассматриваются изотропные линейные среды, не содержащие сегнетоэлектриков и ферромагнетиков. Предварительно сформулируем условия выполнения уравнений Максвелла: 1) эти уравнения макроскопические, т.е. они описывают все электромагнитные явления, в которых не проявляются квантовые эффекты (иначе говоря, на расстояниях больше среднеатомных ~ 10-10м); 2) эти уравнения записаны для достаточно слабых полей, сравнительно медленно изменяющихся в пространстве и во времени, они неприменимы при больших частотах изменения э/м полей, когда становятся существенными квантовые явления; 3) эти уравнения выполняются в среде, для которой энергия э/м поля не превышает энергии теплового (хаотического) движения микрочастиц. Свойства уравнений: • Уравнения Максвелла – линейны. Они содержат только первые производные от характеристик полей Е и В и первые степени плотностей электрических зарядов ρ и токов j. Со свойством линейности непосредственно связан принцип суперпозиции: если два каких-либо поля независимо удовлетворяют уравнениям Максвелла, то это относится и к их сумме. • Уравнения Максвелла – в определенной степени симметричны. Их полная симметричность исключена тем, что в природе существуют электрические заряды, как источники потенциального электрического поля, и отсутствуют анало-гичные «магнитные» заряды, также производные имеют противоположные знаки в соответствующих уравне-ниях и образуют левовинтовую (с вихревым Е -полем) и правовинтовую (с вихревым Н -полем) системы. •
Билет 36. Распространение электромагнитных волн в нейтральной электропроводящей среде. Волновое уравнение и его решение. Скорость электромагнитных волн.
Распространение электромагнитного возмущения
Из теории Дж. Максвелла следует, что переменное электрическое поле порождает вихревое магнитное поле, которое, вообще говоря, тоже оказывается переменным и в свою очередь порождает вихревое электрическое поле и т. д. Таким образом, если возбудить с помощью колеблющихся зарядов (диполя) переменное электрическое поле (∂ D / ∂ t), то в окружающем заряды пространстве возникнет последователь-ность взаимных превращений Е и Н – полей, распростра-няющихся от точки к точке. Этот процесс будет периодичес-ким как во времени, так и в пространстве и, следовательно, представляет собой волну – электромагнитную волну. Вывод волнового уравнения
или с учетом материальных уравнений D = = ε.ε;0. E, B = μ;. μ;0. H Решение волнового уравнения В теории волновых уравнений типа (1, 2) доказывается, что их решения являются гармонические функции вида: ξ;(r, t) = ξm. cos(ω.t – k. r + α;0), где r – радиус-вектор точки в пространстве, ξm - амплитуда волновой функции, ω – циклическая частота волны, k = ω;/ v = 2 π/λ; – волновое число, α;0 – начальная фаза колебаний в точке О.
Вопрос 37. Плоская электромагнитная волна ее уравнение и свойства (E перп H, синфазность(разность фаз =0), поперечность). Связь мгновенных значений векторов E и Н в электромагнитной волне. Рассмотрим плоскую электромагнитную волну, распростра-няющуюся в указанной среде в направлении некоторой оси х (у такой волны волновые поверхности ортогональны оси х, а вектор скорости направлен вдоль х). При этом компоненты Ex-
Вывод волнового уравнения
а также подставив из второго уравнения где 1/ с 2= ε;0. μ;0. Таким образом, мы получили классическое волновое уравнение для компоненты поля Ey.
Решение волнового уравнения В теории волновых уравнений типа (1, 2) доказывается, что их решения являются гармонические функции вида: ξ;(r, t) = ξm. cos(ω.t – k.r + α;0), где r – радиус-вектор точки в пространстве, ξm - амплитуда волновой функции, ω – циклическая частота волны, k = ω;/ v = 2 π/λ; – волновое число, α;0 – начальная фаза колебаний в точке О. Поэтому можно записать решения уравнений (1 и 2) как:
Теория Максвелла не только предсказала возможность существования э/м волн (т. е. особого состояния электромаг-нитного поля, когда оно существует самостоятельно – без электрических зарядов и токов – посредством постоянного преобразования электрического поля в магнитное и т. д.), но и установила основные свойства э/м волн:
2) векторы Е, Н (или В) и v всегда взаимно перпендикулярны и образуют правовинтовую систему; 3) э/м волна – поперечная волна, колебания векторов Дата добавления: 2015-10-12; просмотров: 2987. Нарушение авторских прав; Мы поможем в написании вашей работы! Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар... Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения... Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности... Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
Растягивание костей и хрящей. Данные способы применимы в случае закрытых зон роста.
Врачи-хирурги выяснили...
Экспертная оценка как метод психологического исследования Экспертная оценка – диагностический метод измерения, с помощью которого качественные особенности психических явлений получают свое числовое выражение в форме количественных оценок...
|
Докажем, что: циркуляция вектора магнитной индук-ции по произвольному контуру L равна произведению алгебраической суммы токов, охватываемых контуром, на магнитную постоянную μ0, т.е.
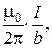Выражение вида (9) получим исходя из закона Био-Савара для случая прямого тока. Пусть ток I направлен за плоскость рисунка. В каждой точке Р контура L вектор В направлен по касательной к окружности радиуса b, проходящей через эту точку. Заменим в выражении для циркуляции произведение B∙dl на B∙dlB (здесь dlB - проекция элемента контура dl на направление В). Из рисунка видно, что dlB ≈ b∙dα (так как dl, dα - малы); тогда, подставив выражение для магнитного поля
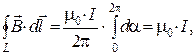прямого тока В = получаем B∙dl = B∙dlB = ∙b∙dα = а последующее
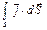Если ток I в формуле (9) распределен по объему, где расположен контур L, то его можно представить через плотность тока j как I = (интеграл по поверхности S, ограниченной контуром L). Тогда уравнение (9) принимает вид:
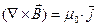
Преобразовав левую часть (10) по теореме Стокса (связь циркуляции вектора В с потоком вектора- rot B, т.е.), получаем равенство: которое должно выполняться при произвольном выборе поверхности S, а это возможно только тогда, когда подынтегральные функции в каждой точке имеют одинаковые значения. Таким образом, получаем: или в проекциях на нормаль
Тот факт, что циркуляция В (или rot B), вообще говоря, не равны нулю, означает, что магнитное поле – не потенциально (в отличие от электростатического поля, для которого
Поток вектора индукции магнитного поля сквозь любую замкнутую поверхность равен нулю:
Используя теорему Остроградского-Гаусса (для перехода от интеграла по поверхности к интегралу по объему) и с учетом (11), приходим к дифференциальной форме теоремы Гаусса для В: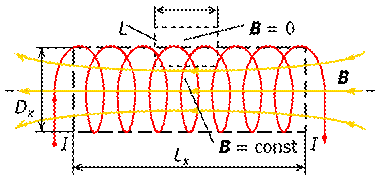
Такой контур охватывает общий ток величиной (N∙I), а циркуляция В в этом случае будет В ∙2 π;∙ r = μ0∙N∙I. Из последнего уравнения определяем искомое поле, которое из-за своей конфигурации принято называть азимутальным:
Если круглый контур проходит вне тора (за пределами его сечения), то никаких токов он не охватывает, циркуляция В∙;2π∙ r = 0 и, следовательно, вне тороида В = 0. Если устремить число витков N и радиус тора Rср в бесконечность, то в пределе из формулы (13) получим выражение для поля соленоида, т. е.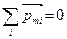
Для объяснения явления намагничения тел Ампер предположил, что в молекулах вещества циркулируют элементарные круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом pmi и создает в пространстве магнитное поле. В отсутствие поля В0 моменты отдельных молекул ориентированы беспорядочно, поэтому их результирующее поле равно 0; соответственно:
Степень намагничивания магнетика характеризуют суммарным магнитным моментом единицы объема вещества и называют эту величину вектором намагниченности:
Поле B’, также как и поле В0, не имеет источников («магнитных зарядов»), поэтому для результирующего поля В при наличии магнетика справедлива теорема Гаусса:
Циркуляция вектора намагниченности
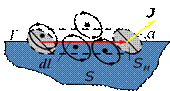
Подставив в последнюю формулу выражение для dV, получаем: dI´= IM.SM.n.cosα.dl = J.cosα.dl =, где учтено, что IM.SM = рm, а рm.n = J. Проинтегрировав последнее выражение для dI´;по контуру Г, приходим к доказываемому положению
Воспользовавшись теоремой Стокса (переход от циркуляции по контуру к потоку ротора через поверхность, натянутую на контур), преобразуем интегральную форму теоремы о циркуляции вектора J в дифференциальную форму. Соответствующее уравнение
должно выполняться для любого контура с площадкой dS в случае, когда его подынтегральные выражения равны, т. е.
В магнетиках, помещенных во внешнее магнитное поле В 0, возникают, как уже установлено, токи намагничивания I´;и, следовательно, для результирующего поля можно записать:
Так как определение токов намагничивания в общем случае задача сложная, то использование формулы (5) для нахождения В становится крайне трудным. Поэтому следует установить некоторый вспомогательный вектор, циркуляция которого определяется только токами проводимости. Заменив в (5) ток I´;через циркуляцию,
Циркуляция вектора Н по произвольному замкнутому контуру равна алгебраической сумме токов проводимости,охватываемых этим контуром, т. е.
Дифференциальная форма получается с помощью теоремы Стокса
Связь между векторами J и H
Для изотропных магнетиков, для которых выполняется (9), определение напряженности (6) может быть записано как
Вводя понятие магнитной проницаемости среды как μ=1+ χ получаем прямую связь двух основных векторов магнитного поля:
Рассмотрим поведение векторов В и Н на границе раздела двух изотропных магнетиков. Эти вектора должны удовлетворять определенным граничным условиям, которые проистекают из: 1) теоремы Гаусса для В, т. е.
и
H 2τ – H 1τ = in, т. е. тангенциальная составляющая вектора Н, вообще говоря, при переходе границы маг-нетиков претерпевает скачок, свя-занный с наличием поверхностных токов проводимости.
В случае, когда i = 0 имеем равенство H 2τ = H 1τ, а для индукции или в виде
Получаем Ei =(v x B). l; произведем циклическую перестановку для смешанного произведения трех векторов в последнем выражении для э.д.с.: Ei =B .(l x v). Умножим и разделим последнее на промежуток времени dt, т. е. имеем
.
Часто последнее свойство взаимной индуктивности называют теоремой взаимности. Смысл равенства L12 = L21 состоит в том, что в любом случае поток Ф1 сквозь контур 1, созданный током I в контуре 2, равен потоку Ф2 сквозь контур 2, созданному таким же током I в контуре 1.
В случае наличия N - связанных контуров с токами I1, I2,…,IN можно показать, что энергия магнитного поля такой системы токов (в отсутствии ферромагнетиков) определяется:
В частности, в случае неподвижного контура и изменяющегося во времени (внешнего) магнитного поля () также возникает э.д.с. в контуре, которую можно трактовать как действие сторонних сил на носители тока. Эти сторонние силы не связаны ни с химическими, ни с тепловыми процессами в проводе, ни с движением контура и, соответственно, действием магнитной силы Лоренца.
Остается заключить, что в этом случае индукционный ток обусловлен возникающим в контуре «особым» электрическим полем Е В, названным Дж. Максвеллом вихревым.
и интегрирование по s можно поменять местами (так как контур и натянутая на него поверхность неподвижны). В итоге получаем:
Воспользовавшись теоремой Стокса (замена циркуляции Е В соответствующим поверхностным интегралом от ротора Е В), преобразуем (2) к виду
Так как выбор поверхности интегрирования S произвольный, то в каждой точке пространства должно выполняться равенство: (3)
Таким образом Дж. Максвелл предположил, что изменяющееся со временем магнитное поле
Поле Е В существенно отличается от электростатического поля Е q, порождаемого неподвижными зарядами q; поле Е q – потенциально, т.е. его силовые линии начинаются и заканчи-ваются на зарядах и для него всегда выполняются равенства:
В общем случае электрическое поле может быть как потен-циальным (Е q), так и вихревым (Е В), и, соответственно, можно записать Е = Е q + Е В, а уравнения (2) и (3) представить как:
Известно, что согласно теореме о циркуляции вектора напряженности магнитного поля Н:
Дж. Максвелл предложил ввести дополнительное слагаемое в правую часть уравнения (5), которое он назвал током смещения Iсм, и тогда в общем случае циркуляция вектора Н
Ток смещения Iсм должен зависеть от производной характеристики электрического поля по времени, т.е. от
Так как (см. рисунок) поверхность S2 «пронизывает» только электрическое поле конденсатора, причем – переменное, поскольку оно определяется «мгновенным» зарядом q (t) на обкладках, то по теореме Гаусса
и, следовательно, нужно рассмотреть производную от этого уравнения: (7) (8)
Это уравнение аналогично уравнению непрерывности для постоянного тока; Максвелл, записав его в таком виде, определил дополнительное слагаемое как плотность тока смещения с размерностью [А/м2].
Сумму тока проводимости I и тока смещения Iсм называют полным током Iпол = I + Iсм или для плотности тока: j пол = j + j см = j +
Т. об. теорему о циркуляции вектора Н следует записывать в более общем виде (обобщение на переменные во времени токи и поля) – в форме закона полного тока: (10)
Дифференциальной формой закона полного тока является уравнение: (11)
Ток смещения j см равнозначен току проводимости j только по способности создавать магнитное поле. В определенной степени термин «ток смещения» является чисто условным. По существу j см – это изменяющееся во времени электрическое поле, т.е. Иначе говоря, токи смещения существуют лишь там, где изменяется со временем электрическое поле.
Замечание. В диэлектриках ток смещения состоит из двух существенно различных слагаемых. Так как D = ε0 E + P, то J см =,
где - собственно плотность тока смещения, обусловленного изменением электрического поля; - плотность тока поляризации, обусловленного перемещением связанных зарядов в ходе поляризации диэлектрика.
Уравнения Максвелла – релятивистки инвариантны (относительно преобразований Лоренца). Вид уравнений не меняется при переходе от одной инерциальной системы отсчета К к другой К’, движущейся со скоростью v относительно первой вдоль общей оси 0х. Однако входящие в уравнения величины (Е, В и др.) преобразуются по определенным правилам (согласно преобразованиям Лоренца). Так в проекциях на оси xyz имеем:
Существование электромагнитных (э/м) волн вытекает из уравнений Максвелла. Так в случае однородной (ε;, μ; = const) электрически нейтральной (ρ = 0) и непроводящей (σ = 0) среды имеем уравнения в симметричной форме:
Скорость распространения э/м волны в непроводящей, нейтральной, неферромагнитной среде подчиняется соотношению
Нх-полей не зависят ни от х, ни от t, они постоянны и обычно полагают: Ех= Нх = 0. В этом случае система* принимает вид:
Для описания плоской э/м волны достаточно взять одну пару уравнений, например, (а), положив Еz = Нy = 0.
Продифференцировав первое уравнение из (а) по х и произведя перестановку операций в его правой части, т. е.
Проделав аналогичные операции со вторым уравнением системы (а) получаем волновое уравнение для компоненты Hz:
Подставив решения (3) в уравнения Максвелла системы (а), получаем k.Em. sin(ω.t –k.x + α1) = μ;. μ;0.ω. Hm. sin(ω.t –k.x +α2) и k.Hm. sin(ω.t – k.x + α2) = ε.ε;0. ω.Em. sin(ω.t – k.x + α1). Для того, чтобы эти уравнения удовлетворялись, необходимо равенство α1 = α2 и должны выполняться соотношения: k.Em= μ.μ;0 .ω.Hm и ε.ε;0 .ω.Em= k.Hm. Если последние равенства перемножить слева и справа, то ε.ε;0 .Em 2 = μ.μ;0. Hm 2 или
