Возможности
1. Рисуем расчетную схему. Указываем на ней направления скоростей каждого тела.
2. Вычисляем скорость груза 1
В момент времени 3. Вычисляем ускорение груза 1
4. Для определения угловой скорости
Отсюда 5. Запишем уравнение, связывающее угловые скорости колес 2 ω 2 и 3 - ω 3.
Откуда вычисляем- ω 3
или с учетом (5) после подстановки данных
В момент времени t1 Угловое ускорение колеса 3
6. Определим скорость точки М, её центростремительное, вращательное и полное ускорения
Рис.2
Результаты вычислений для заданного момента времени
Скорости и ускорения тела 1 и точки М показаны на рис. 2.
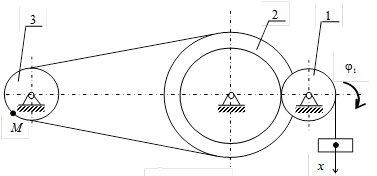
Пример 2 Рассмотрим пример решения задания для механизма, кинематическая схема которого приведена на рис. 3., где ведущим звеном является груз. Задано: закон изменения вертикальной координаты груза x (t) = 30 + 10 t 2, см; радиусы колес R1 = R3 = 10 см, R2 = 30 см, r2 = 20 см. Определить скорость и ускорение точки М для момента времени t1 = 1 c.
Рис.3 Решение Обозначим и покажем на рис.3 точки механизма А, В, D1, D2, через которые передается движение от одного звена (ведущего) к другому (ведомому). Решение задачи начнем с определения скорости груза. Поскольку груз совершает поступательное движение, его можно считать точкой, движение которой задано координатным способом, и движется только вдоль оси x. Проекцию скорости груза на эту ось определим как производную от координаты x по времени
Поскольку знак проекции скорости груза на ось x положительный, вектор скорости направлен вниз, т.е. в положительном направлении оси x.
Рис.4 Скорости всех точек нити, на которой висит груз, одинаковы (нить считается нерастяжимой), скорость точки схода нити с барабана (колеса 1) равна скорости груза. Но точка А схода нити в данный момент времени принадлежит и колесу 1, совершающему вращательное движение вокруг неподвижной оси, что позволяет определить его угловую скорость. Направление угловой скорости колеса 1 соответствует направлению скорости точки А. Запишем теперь алгебраическое значение угловой скорости колеса 1
Колеса 1 и 2 находятся в зацеплении и имеют общую точку В (см. рис.4). Поэтому скорости точек колес, находящихся на их ободьях, одинаковы. При записи алгебраического значения угловой скорости колеса 2 учтем, что внешнее зацепление меняет направление вращения на противоположное
Одинаковы также скорости точек D1 и D2, расположенных на шкивах ременной передачи. Однако здесь направление вращения не изменяется, поэтому
Определим теперь скорость точки M колеса 3 в момент времени t 1 = 1 с. Величина скорости – это произведение модуля угловой скорости на расстояние от точки M до оси вращения, которое равно радиусу
откуда получим полное ускорение точки M
Векторы ускорений показаны на рис. 5. Движение колеса 3 ускоренное, поэтому вращательное ускорение точки M направлено в ту же сторону, что и ее скорость. Центростремительное ускорение всегда направлено к оси вращения. Если в условии будет задан не закон движения груза x(t), а зависимость угла поворота колеса 1 от времени, например, j 1(t) = 3 +t 2, рад, изменения в решении задачи коснутся только начального этапа. Алгебраическое значение угловой скорости колеса 1 определим как производную от его угла поворота по времени Дальнейшее решение задачи не отличается от приведенного примера.
ПРИМЕРЫ РЕШЕНИЯ КОНТРОЛЬНОГО ЗАДАНИЯ К3 Пример 1. Катушка катится без скольжения в вертикальной плоскости по наклонному пути (рис. К3-1).
r = 0.6 м, R = 1 м. Решение Катушка совершает плоскопараллельное движение. Так как качение происходит без скольжения, то скорость точки Р касания катушки с неподвижной поверхностью
где
Определим угловую скорость катушки
Так как скорости точек О и В катушки также пропорциональны их расстояниям до точки Р, то
Направление вращения катушки, а, следовательно, и направления скоростей точек В и О, определяются направлением вектора скорости Пример 2. Стержень АВ имеет на концах ползуны, один из которых А скользит по прямолинейной направляющей со скоростью Найти в положении, указанном на рис. К3-2, угловую скорость стержня, скорости точек В и С, если АВ = 1, 2 м, АС = ВС.
Решение Стержень АВ совершает плоскопараллельное движение. Так как скорости точек А и В направлены параллельно соответствующим направляющим, вдоль которых скользят ползуны, то, восстанавливая из точек А и В перпендикуляры к скоростям этих точек, определим положение мгновенного центра скоростей стержня АВ – точка Р. Треугольник АВР является равнобедренным, следовательно, АВ = ВР = 1, 2м. Скорость точки А пропорциональна расстоянию от этой точки до точки Р: Вычислим угловую скорость стержня АВ
Скорость точки В определим по формуле
Для определения скорости точки С найдем расстояние РС с помощью теоремы косинусов
Тогда скорость точки С
Пример 3. Кривошип ОА длиной r = 1 м вращается с угловой скоростью Определить скорость ползуна В, угловую скорость шатуна
Рис.К3-3 Решение Шатун АВ совершает плоскопараллельное движение. При этом
Найдем положение мгновенного центра скоростей, восстанавливая перпендикуляры к скоростям точек А и В из этих точек. При угле j = 0 (см. рис. К3-3, а) перпендикуляр к скорости
На рис. К3-3, а показано распределение скоростей точек шатуна. При угле поворота кривошипа j = 900 скорости Пример 4. Кривошип ОА = 0, 5м вращается с угловой скоростью w 0А = 10 рад/с и приводит в движение шатун АВ = 4 м. Найти угловую скорость шатуна, скорости точек В и С (АС = 2, 5м), если угол поворота кривошипа j = 450 и ОА ^ АВ (рис.К3-4). Решение Так как кривошип ОА совершает вращательное движение, то
Найдем угловую скорость шатуна АВ
Скорости точек В и С пропорциональны их расстояниям до МЦС:
где ВР =
Возможности. 1. Выход на новые сегменты рынка 2. Расширение производственной линии 3. Добавление сопутствующих товаров и услуг 4. Вертикальная интеграция 5. Ускорение темпов роста рынка 6. Возможность перейти в группу лидеров рынка 7. Ослабление конкурентов Угрозы 1. Возможность появление новых конкурентов 2. Рост продаж замещающего продукта 3. Замедление темпов роста рынка 4. Неблагоприятная политика правительства 5. Возросшая конкурентная давление 6. Возрастания сила торга у потребителей и поставщиков 7. Изменение потребностей и вкуса покупателей 8. Неблагоприятные демографические изменения При анализе сильных и слабых сторон их список должен соответствовать функциональным сферам организации. При анализе возможностей и угроз рассматриваются все составляющие макро и непосредственные окружения. Кроме SWOT есть SNW- он предназначен только для анализа внутренней среды (сильные, нейтральные, слабые стороны) STEP PEST- для внешней.
|

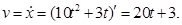
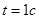 скорость равна
скорость равна 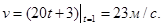
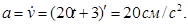
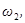 и углового ускорения тела 2 запишем уравнение, связывающее скорость груза v и угловую скорость колеса 2. ω 2 и ω 3. В соответствии со схемой механизма
и углового ускорения тела 2 запишем уравнение, связывающее скорость груза v и угловую скорость колеса 2. ω 2 и ω 3. В соответствии со схемой механизма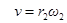
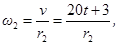
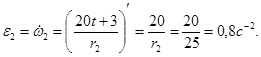
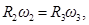
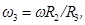


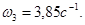
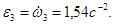

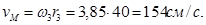
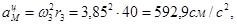
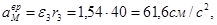
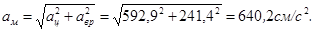
 с приведены в таблице
с приведены в таблице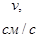
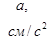
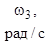

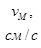
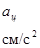
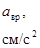

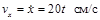 , при t 1 = 1 с vx= 20 см/с.
, при t 1 = 1 с vx= 20 см/с.
 , при t 1 = 1с w1 z= 2рад/с.
, при t 1 = 1с w1 z= 2рад/с. , при t 1 = 1 с w2 z = 1рад/с.
, при t 1 = 1 с w2 z = 1рад/с. , при t 1= 1 с
, при t 1= 1 с 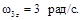
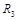 ,
, 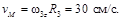 Направление вектора скорости покажем перпендикулярно радиусу, соединяющему точку с осью вращения, в соответствии с направлением вращения (рис. 4).
Направление вектора скорости покажем перпендикулярно радиусу, соединяющему точку с осью вращения, в соответствии с направлением вращения (рис. 4).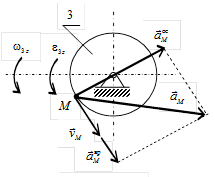 Для нахождения ускорения точки M необходимо знать угловое ускорение колеса 3. Алгебраическое значение углового ускорения определим как производную по времени от алгебраического значения угловой скорости
Для нахождения ускорения точки M необходимо знать угловое ускорение колеса 3. Алгебраическое значение углового ускорения определим как производную по времени от алгебраического значения угловой скорости 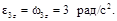 Алгебраические значения угловой скорости и углового ускорения имеют одинаковые знаки, следовательно, вращательное движение является ускоренным.
Алгебраические значения угловой скорости и углового ускорения имеют одинаковые знаки, следовательно, вращательное движение является ускоренным. Ускорение точки M определим как геометрическую сумму векторов вращательного и центростремительного ускорений, модули коРис.5 торых вычислим по формулам:
Ускорение точки M определим как геометрическую сумму векторов вращательного и центростремительного ускорений, модули коРис.5 торых вычислим по формулам: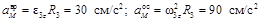 ,
,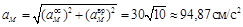 .
.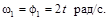
 Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент времени
Найти угловую скорость катушки, скорости точек О и В, если в рассматриваемый момент времени  = 2 м/с,
= 2 м/с,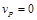 , следовательно эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А
, следовательно эта точка является мгновенным центром скоростей (МЦС). Вектор скорости точки А 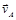 перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости пропорционально расстоянию от точки А до МЦС:
перпендикулярен АР и направлен в сторону качения катушки, а численное значение скорости пропорционально расстоянию от точки А до МЦС: ,
,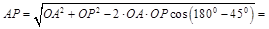
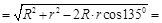 1, 49 м.
1, 49 м.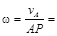 1, 35 рад/с.
1, 35 рад/с. 0, 81 м/с;
0, 81 м/с;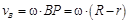 = 0, 54 м/с.
= 0, 54 м/с.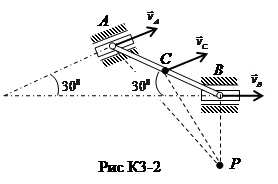
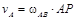 , где
, где  2, 08 м.
2, 08 м.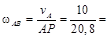 0, 48 рад/с.
0, 48 рад/с.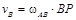 = 0, 48·1, 2 = 0, 58 м/с.
= 0, 48·1, 2 = 0, 58 м/с. 1, 59 м.
1, 59 м.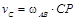 = 0, 76 м/с.
= 0, 76 м/с.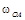 = 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как показано на рис. К3-3.
= 2 рад/с, приводя в движение шатун АВ длиной l = 4 м, как показано на рис. К3-3. в двух положениях механизма, когда угол поворота кривошипа j = 0 и j = 900.
в двух положениях механизма, когда угол поворота кривошипа j = 0 и j = 900.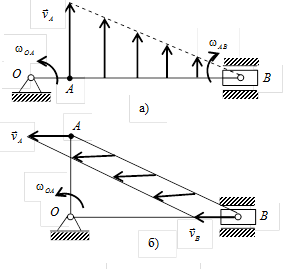
 , так как точка А принадлежит кривошипу ОА, совершающему вращательное движение. Скорость ползуна В параллельна направляющим. Численное значение скорости точки А
, так как точка А принадлежит кривошипу ОА, совершающему вращательное движение. Скорость ползуна В параллельна направляющим. Численное значение скорости точки А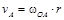 =2·1=2 м/с.
=2·1=2 м/с. пересекаются в точке В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей и
пересекаются в точке В. Следовательно, точка В является в этом положении механизма мгновенным центром скоростей и  . Это положение механизма называют «мертвым». Найдем угловую скорость шатуна
. Это положение механизма называют «мертвым». Найдем угловую скорость шатуна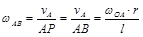 = 0, 5 рад/с.
= 0, 5 рад/с.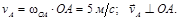
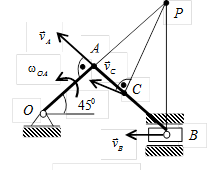 Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м.
Шатун АВ совершает плоскопараллельное движение. Найдем мгновенный центр скоростей для данного положения шатуна – точку Р на пересечении перпендикуляров к скоростям точек А и В, восстановленных из этих точек. Треугольник РАВ равнобедренный, при этом АВ = АР = 4 м.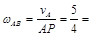 1.25 рад/с.
1.25 рад/с.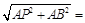
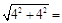 5, 65 м;
5, 65 м;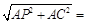
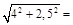 4, 72 м;
4, 72 м;


