Важнейшие способы обработки и анализа рядов динамики
Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени. В этих случаях ряд динамики подвергается дополнительной обработке различными способами. 1. Приведение ряда динамики к одному основанию применяется для сравнения изменения одного показателя для различных объектов во времени. Пример: имеются данные о закупках молока в двух санаториях в 1999–2003 гг.
2. Метод скользящей средней используется для устранения влияния случайных факторов на динамику изучаемого явления, процесса. Его сущность заключается в определении подвижных сумм, путем последующего сдвига на одну дату суммируемого показателя; затем подвижные суммы делятся на число дат, таким образом получаются подвижные, или скользящие средние величины.
Основное направление развития явления во времени называется трендом. 3. Выравнивание по аналитическим формулам. Суть этого способа состоит в том, что по эмпирическим данным находят так называемое уравнение тренда, по которому определяют теоретические уровни, рассматриваемые как функция времени, т.е.
Рис. 9. Графическое определение линии тренда
Нахождение параметров той или иной гипотетической функции осуществляется аналогично нахождению параметров уравнений регрессии (в качестве фактора x выступает фактор времени t). Так, при выравнивании ряда по прямой для нахождения параметров прямой решается система нормальных уравнений вида
Для упрощения рассчета при выравнивании динамических рядов условное обозначение временных точек (t) можно ввести так, чтобы. В этом случае системы нормальных уравнений значительно упрощаются. Так, при выравнивании по прямой система будет иметь вид
Пример. Имеются следующие данные о прибытиях туристов в города за 5 лет (на начало года):
Найти линию тренда и, используя полученное уравнение, определить численность туристов в 2006 г. (прогноз). Если время (t) обозначить так, чтобы
Каждое уравнение в этом случае решается самостоятельно:
Необходимые для расчета а0 и а1 суммы приведены в таблице.
Получаем 5а0=410, а0=82; 10а1=45, а1=4,5, отсюда уравнение прямой для выровненных уравнений (линия тренда):
Выровненные значения, рассчитанные по последней формуле путем постановки в нее значений t=-2, -1, 0, 1, 2, показаны в графе 6 таблицы. Численность туристов в 2006 г. (t=5) определяем по формуле:
Естественно, эта величина условная, рассчитанная при предположении, что линейная закономерность изменения численности населения, принятая для 1999–2003 гг., сохранится на следующий период до 2006 г. 4. Интерполяция – это метод определения неизвестных промежуточных значении ряда динамики на основе анализа известных показателей. Пример. Имеются данные о производстве электроэнергии в регионе в 1998–2003 гг. Представим, что за 2001 г. нет данных. Найдем их тремя способами.
1. Определим среднегодовой прирост за 2000–2002 гг.:
тогда 2. Определим темп роста: , тогда 3. Определим среднегодовой темп роста за весь период:
тогда 5. Экстраполяция – распространение результатов наблюдения над определенными объектами на объекты, не подвергшиеся наблюдению (прогнозирование явлений). Рассмотрим методы на предыдущем примере. Предположим, что нам необходимо сделать прогноз на 2003 г. 1. Определим среднегодовой абсолютный прирост:
2. Определим среднегодовой темп роста:
Методы интерполяции и экстраполяции применяются только в случаях плавного, постепенного, равномерного изменения явления на небольших промежутках времени.
|

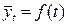 .
.
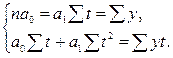
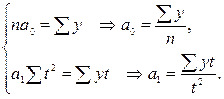
 (т.е. счет вести от середины ряда), то система упростится и примет вид
(т.е. счет вести от середины ряда), то система упростится и примет вид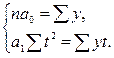
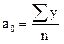 и
и 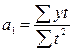 .
.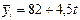

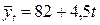 .
. .
.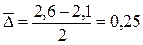 ,
,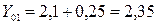
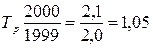
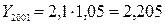
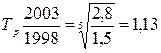 ,
,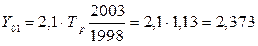
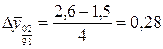 ,
,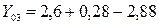 .
.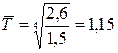 ,
,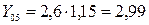 .
.


