Основные показатели изучения динамических рядов
К числу основных показателей динамических рядов относятся: 1. Темп роста. Различают базисный и цепной темпы роста: а) базисный – отношение последующего показателя к первоначальному, принятому за базу:
б) цепной – отношение последующего показателя к предыдущему:
2. Темп прироста. Существует два вида темпа прироста: а) базисный – разница между базисным темпом роста и 1 или 100%:
показывающий, на сколько процентов изменился каждый последующий показатель по сравнению с первоначальным или другим, принятым за базу сравнения; б) цепной:
Показывает, на сколько процентов изменился последующий показатель по сравнению с предыдущим. Другой способ: Между цепными и базисными темпами роста имеют место определенные зависимости: – Произведение последующих цепных темпов роста равно соответствующему базисному темпу роста:
– Отношение последующего базисного темпа роста к предыдущему равно цепному темпу роста:
– Среднегодовой темп роста определяется по формуле средней геометрической: а) где n – число темпов роста. б) где Yi – последний уровень ряда динамики; Y0 – первоначальный уровень ряда динамики; n – количество темпов роста (периодов). Показывает, во сколько раз в среднем за год изменился изучаемый показатель. 3. Среднегодовой темп прироста:
Показывает, на сколько процентов в среднем за год изменился изучаемый показатель. 4. Абсолютный прирост: а) базисный: Дyб=yi – y0 ДYБ=Y i– Y0. б) цепной: Дyц=yi – yi-1 ДYЦ=Yi – Yi-1. Показывает на сколько единиц изменился каждый последующий уровень динамического ряда по сравнению с базисным или предыдущим. 5. Среднегодовой абсолютный прирост:
где n – число дат.
где yn – последний уровень ряда динамики; y0 – первоначальный уровень р.д.; n – число уровней. Показывает, на сколько единиц в среднем за год изменился изучаемый показатель. 6. Средний уровень ряда динамики: а) для интервальных рядов средних величин и относительных величин.
б) для моментных рядов.
7. Абсолютное содержание 1% прироста: 1) 2)
|

 ;
; .
. , или,
, или, 
 .
. .
.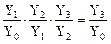 .
.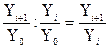 .
. ,
, ,
, .
. ,
,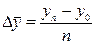 ,
, ;
; .
. .
.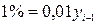 .
.


