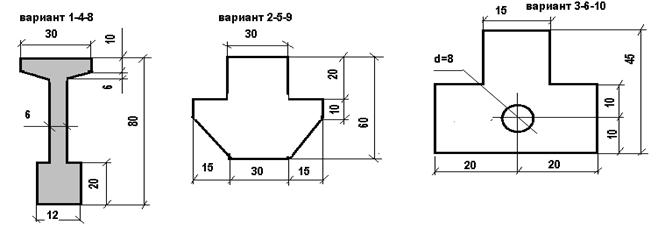
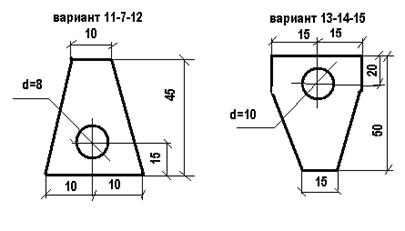
ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ
Сила, с которой тело притягивается к Земле, называется силой тяжести. Центром тяжести тела называется центр параллельных сил тяжести всех элементарных частиц тела. Центр тяжести есть геометрическая точка, которая может лежать вне тела (например, кольцо, цилиндр с отверстием). Координаты центра тяжести находят по формулам: хс = ∑ (Gixi)/ ∑ Gi; yс = ∑ (Giyi)/ ∑ Gi где хс, yс - координаты частицы; ∑ Gi - сила тяжести всего тела в случае однородных тел по таким же формулам можно определить координаты центра тяжести объемов, площадей и линий. Центр тяжести определяют методами: метод симметрии, метод разбиения, метод отрицательных масс, метод взвешивания Метод симметрии опирается на положения: 1. Если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости; 2. Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси; 3. Если однородное тело имеет две оси симметрии, то центр тяжести тела лежит в точке их пересечения; 4. Центр тяжести однородного тела вращения лежит на оси вращения. Метод разбиения заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют известные формулы: хс = ∑ (Gixi)/ ∑ Gi; yс = ∑ (Giyi)/ ∑ Gi Метод отрицательных масс. Этот метод заключается в том, что тело, имеющее свободные полости, полагают сплошным, а массу свободных полостей считают отрицательной. Вид формул для определения координат центра тяжести при этом не меняется.
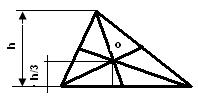
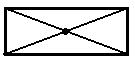
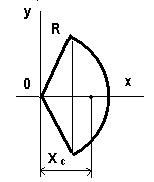
Положения центра тяжести некоторых фигур: 1. Прямоугольник – центр тяжести лежит в точке пересечения его диагоналей. 2. Треугольник – центр тяжести лежит в точке пересечения его медиан, на расстоянии одной трети высоты от каждого основания. 3. Дуга окружности: Xc = (Rsinα /) α 4. Круговой сектор: Xc = (2Rsin α /) 3α
Порядок определение положения центра тяжести плоской фигуры: 1. Разбивают сечение на простые фигуры. 2. Указывают центры тяжести каждого профиля (фигуры) и обозначают их С1 С2,..., Сп, 3. Выбирают систему координатных осей. В задачах для самостоятельной работы все сечения имеют одну ось симметрии, по этому рекомендуется одну из координатных осей совмещать с ней. Вторую ось координат направляют перпендикулярно первой так, чтобы она пересекла центры тяжести одной или нескольких фигур. При этом начало координат может совпадать (или не сов падать) с центром тяжести одной из фигур. Вторую ось можно направить так, чтобы она прошла через нижнюю (крайнюю) точку сечения. В первом случае вычисления будут более простыми. 4. Составляют формулы для определения координат центра тяжести сечения: A1x1 + A2x2 +A3x3 + … + Anxn Xc = ---------------------------------- (1) A1+A2+A3+ … + An
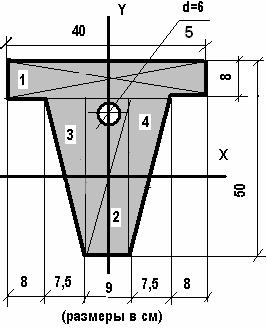
A1y1 + A2y2 +A3y3 + … + Anyn Yc = ---------------------------------- (2) A1+A2+A3+ … + An Где А1, А2, А3 – площади профилей; х1, х2, х3, …у1, у2, у3 - координаты их центров тяжести относительно выбранных осей координат. Число слагаемых в числителе и знаменателе формул зависит от числа профилей, из которых состоит сечение. Полученные величины подставляют в формулу и находят хс и ус. Следует помнить, что если ось х совмещена с осью симметрии, то координата ус= 0, а если ось усовмещена с осью симметрии, то хс = 0. 5. Указывают положение центра тяжести на рисунке, придерживаясь определенного масштаба, и показывают расстояние от центра тяжести до координатных осей. 6. Выполняют проверку правильности решения, для чего можно изменить положение координатных осей (или одной оси) и найти координаты центра тяжести относительно новых осей. Положение центра тяжести не зависит от того, как выбрана система координатных осей. ПРИМЕР: Определить положение центра тяжести сечения, состоящего из простых геометрических фигур. РЕШЕНИЕ: 1. Разобьем сечение на простые фигуры: прямоугольник (1), прямоугоник (2), треугольники -3 и 4, круг -5. 2. Укажем центры тяжести полученных простых фигур – С1, С2, С3, С4, С5. 3. Выберем систему координат. Ось Х проведем через центр тяжести С2 прямоугольника 2 (в виду симметричности фигуры, ее центр тяжести лежит на оси симметрии, т.е. Хс =0), а ось У совместим с осью симметрии сечения (она пройдет через центры тяжести круга 5, прямоугольника 1). 4. Определим площади отдельных фигур и их центры тяжести: · Прямоугольник 1 А1 = 40*8 = 320 см2 Х1 = 0; У1= (50-8)/2 + 8/2 =25 см · Прямоугольник 2 А2 = 9(50-8) = 378 см2 Х2 =0; У2=0 · Треугольник 3, 4 А3 = А4= 7, 5(50-8)/2 = 157, 5 см2 У3=У4 = (50-8)/2 – (50-8)/3 = 7 см
· Круг -5 А5 = π d2/4 = 3, 14*6*6/4= 28, 3 см2 У5 = (50\2) – 6\2 = 18 см; Х5 = 0 5. Определяем центр тяжести фигуры:
A1y1 + A2y2 + 2A3y3 - A5y5 Yc = ---------------------------------- = A1+A2+ 2A3- A5
(320*25+378*0 +2*157, 5*7 – 28.3*180) (320+378+2*157, 5-28, 7) = = 9, 84 см; Хс = 0
ЗАДАНИЕ: в соответствии со своим вариантом провести расчет координат центра тяжести плоской фигуры.
|

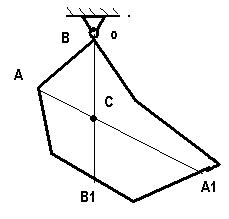 Метод подвешивания. Если тело в виде пластины любой формы подвесить на нити в любой точке (например А), то при равновесии центр тяжести тела обязательно займет положение по вертикали, проходящей через точку А, так как при таком положении центра тяжести сила тяжести и реакция нити уравновешивают друг друга. С помощью отвеса отметим на теле линию А-А1, на которой расположен искомый центр тяжести. Подвесив затем тело на нити в другой точке, например В, получим линию В-В1, которая пересечением с линией А-А1 фиксирует положение центра тяжести – точку С.
Метод подвешивания. Если тело в виде пластины любой формы подвесить на нити в любой точке (например А), то при равновесии центр тяжести тела обязательно займет положение по вертикали, проходящей через точку А, так как при таком положении центра тяжести сила тяжести и реакция нити уравновешивают друг друга. С помощью отвеса отметим на теле линию А-А1, на которой расположен искомый центр тяжести. Подвесив затем тело на нити в другой точке, например В, получим линию В-В1, которая пересечением с линией А-А1 фиксирует положение центра тяжести – точку С.