Работа силы на криволинейном перемещении
При криволинейном движении формулой
Интегрируя или суммируя элементарные работы на конечном отрезке пути, получаем полную работу:
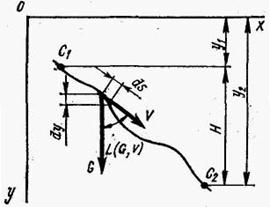
Используем эту формулу для вычисления работы силы тяжести. Пусть некоторая точка, сила тяжести которой G, переместилась по криволинейной траектории из точки С1 в точку С2, опустившись на высоту Н
Из рисунка следует, что
Формула для работы принимает вид:
Вынося из-под знака суммы постоянную величину — силу тяжести тела G — и учитывая, что сумма элементарных перемещений вдоль оси у равна полной высоте перемещения тела
т. е. работа силы тяжести равна произведению силы тяжести на вертикальное перемещение ее точки приложения. Таким образом, работа силы тяжести не зависит от траектории, по которой перемещается центр тяжести тела.
|
пользоваться нельзя. В этом случае пользуются понятием элементарной работы на бесконечно малом участке нути ds, 
который можно считать прямолинейным,
где v — скорость точки, совпадающая по направлению с элементарным перемещением.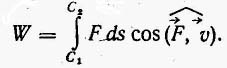
.
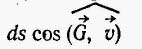представляет собой проекцию элементарного перемещения на направление силы G, т. е.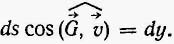
, получаем:
