РЕШЕНИЕ СТАТИЧЕСКИ ОПРЕДЕЛЕННЫХ ЗАДАЧ О РАВНОВЕСИИ СИСТЕМЫ ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ

 

Установленные для различных случаев расположения сил уравнения равновесия позволяют составить для каж­дого случая только определенное число сил, независимых урав­нений, налагающих соответствующие условия на систему находящихся в равновесии сил.

Мы можем, конечно, проецируя силы на различные оси и составляя уравнения моментов относительно раз­личных центров, написать сколько угодно уравнений, но независимыми из них будут только три для общего случая плоской системы и только два для частных случаев пло­ской системы—сходящихся или параллельных сил.

Задачи, в которых число неизвестных величин не пре­вышает числа независимых уравнений равновесия, даваемых статикой твердого тела для данного случая расположения сил, называются статически определенными задачами, в противном случае задачи называются статически неопре­деленными. Методы решения статически неопределенных задач рассматриваются в сопротивлении материалов.

При решении задач статики обычно исходят из того, что рассматриваемое в задаче тело находится в покое и, значит, согласно первой аксиоме на него действует уравновешенная система внешних сил. Приступая к решению такой задачи, где на тело действует произвольная плоская система сил, мы заранее знаем, что усло­вие равновесия выполняется, т. е. если произвольная плоская система сил уравновешена, то ее глав­ный вектор равен нулю и алгебраическая сумма моментов всех сил относительно любой точки также равна нулю.

 

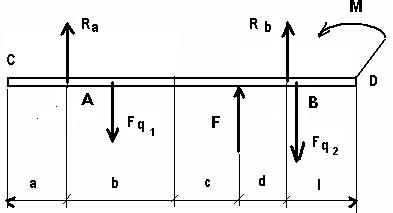
Первая форма уравнений равновесия вытекает непосредственно из условия, определяющих необходимое и достаточное усло­вие равновесия плоской системы сил.

∑ F_kx = 0; ∑ F_ky = 0; ∑ M₀(F_k) = 0 (1)

Следовательно, если плоская система сил уравновешена, то алге­браическая сумма проекций всех сил на оси X и Y равна нулю, а также равна нулю алгебраическая сумма моментов всех сил относительно любой точки.

Уравнений равновесия три, т.е. в произвольной плоской уравновешенной системе число неизвестных сил не должно превышать трех.

Вторая форма уравнения равновесия получается, если вместо одного уравнения моментов составить два:

∑ M_А(F_k) = 0; ∑ M_В(F_k) = 0; ∑ F_kx = 0 (2)

и к ним добавить одно уравнение проекций на любую ось.

Следовательно, если произвольная плоская система сил уравновешена, то алгебраическая сумма моментов сил относительно двух любых точек, а также алгебраическая сумма проекций сил на ось, не перпендикулярную прямой, проходящей через эти точки, равны нулю.

Третья форма уравнения равновесия получается, если вместо урав­нения проекций к двум уравнениям моментов относительно двух произвольно взятых точек А и В добавить третье уравнение моментов сил относительно какой-либо точки С, не лежащей на прямой АВ:

∑ M_А(F_k) = 0; ∑ M_В(F_k) = 0; ∑ M_С(F_k) = 0; (3)

т. е. если произвольная плоская система сил уравновешена, то ал­гебраические суммы моментов сил относительно любых трех точек, не лежащих на одной прямой, равны нулю.

ПРИМЕР РЕШЕНИЯ: Определить опорные реакции балки, изображенной на рисунке.

ДАННЫЕ ЗАДАЧИ:

M = 25 Hм; q₁ = 20 Нм

q₂ = 15 Нм; F = 30 Нм;

а =1 м; b = 3, 5 м;

c = 1 м; d = 1, 5 м;

l = 1, 5 м

 

 

РЕШЕНИЕ:

1. Заменяем распределенную нагрузку равнодействующей

F_q1 = q₁ (a+b) = 20(1+3.5) = 90 кH

(сила F_q1 приложена в середине отрезка (а +b) на расстоянии (b-a)/2 от опоры А)

F_q2 = q₂ (d+l) = 15(1.5+1.5) = 45 кH

(сила F_q2 приложена в середине отрезка (d+l))

2. Определим направление опорных реакций с учетом типа опоры – шарнирная

3. Составляем уравнения равновесия балки:

∑ F_kx = 0; ∑ F_ky = 0; ∑ M_A(F_k) = 0

 

R_A –F_q1 + F + R_B – F_q2 = 0 (1)

 

R_A - 90 + 30 + R_B – 45 = 0; R_A+ R_B = 105 Кн.

- М_А(F_q1) + М_А (F) + М_А(R_B) - М_А(F_q2) + М = 0 (2)

-90*1, 25 + 30*4, 5 + R_B* 6 – 45*6 + 25 = 0 R_B = 37, 08 кН

R_A = 105 - R_B = 105 - 37, 08 = 67, 92 кН

 

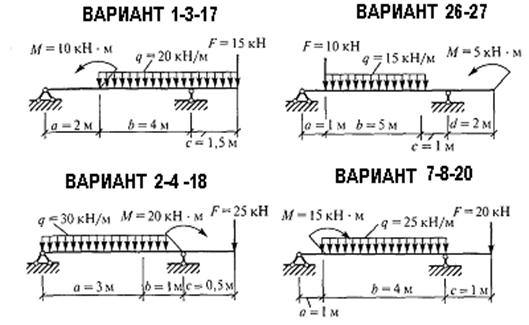
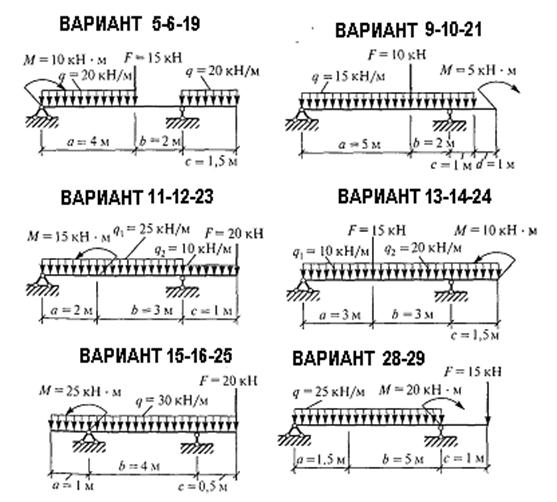
Реакции опор вертикальные и составляют 37, 08 и 67, 92 кН

ЗАДАНИЕ: В соответствии с вариантом (см. таблицу) определить опорные реакции балки, использовав все формы уравнений равновесия (3 решения одной задачи)