АНАЛИТИЧЕСКИЙ СПОСОБ РЕШЕНИЯ
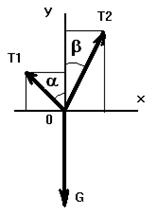
Возьмем начало координат в точке С, равновесие которой мы рассматриваем. Направим ось у – вертикально вверх. Углы (Т1, у) = ά =45о и (Т2, у)= β = 30о. Находим значения проекций всех сил на выбранные координатные оси и заносим для удобства в таблицу. Таблица
Уравнения равновесия принимают в данном случае вид
∑ Yк = - G + Т1 cos 45о + Т2 cos 30о = 0 cos 45о = √ 2 /2 = 0, 707, cos 60о = 0, 5, cos 30о = √ 3 / 2 = 0, 866 и G= 20 Н. Подставляя найденные значения, получим - 0, 707 Т1 + 0, 5 Т2 = 0; - 2 + 0, 707 Т1 + 0, 866 Т2 = 0. Решая эту систему уравнений, находим Т2 = 20/ 1, 366 = 14, 6 Н, Т1 = 0, 5 х 14, 6 / 0, 707 = 10, 3 Н. ЗАДАНИЕ: Всоответствие со своим вариантом и данных таблицы провести расчет (геометрическим, графическим и аналитическим методом) реакций связей.
Стержни АВ и ВС соединены между собой и вертикальной стеной посредством шарниров. Определить реакции стержней АВ и ВС на шарнирный болт В, если к нему подвешен груз весом G.
Таблица вариантов
|
∑ Xк = - Т1 cos 45о+ Т2 cos 60о = 0,
