Теория усилителей. Схема
Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах – операционных усилителях(условное графическое обозначение и примеры реализации приведены на рис. 6.3). Операционный усилитель (ОУ) – унифицированный многокаскадный усилитель постоянного тока, выполненный на интегральной схеме и удовлетворяющий следующим требованиям к электрическим параметрам: - коэффициент усиления по напряжению стремится к бесконечности (KU → ∞); - входное сопротивление стремится к бесконечности (RВХ → ∞); - выходное сопротивление стремится к нулю (RВЫХ → 0); 41- если входное напряжение стремится к нулю, то выходное напряжение также равно нулю (UВХ = 0 → UВЫХ = 0); - бесконечная полоса усиливаемых частот (fВ → ∞) Являясь, по существу, идеальным усилительным элементом, ОУ составляет основу всей аналоговой электроники, что стало возможным в результате достижений современной микроэлектроники, позволившей реализовать достаточно сложную структуру ОУ в интегральном исполнении на одном кристалле и наладить массовый выпуск подобных устройств. Все это позволяет рассматривать ОУ в качестве простейшего элемента электронных схем подобно диоду, транзистору и т.п.
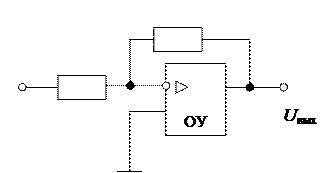
Рис. 6.3. Операционный усилитель: обозначение на схемах и реальные устройства Основные типы схем на базе ОУ: Инвертирующий усилитель. Подключив звено отрицательной обратной связи (ООС), состоящее из двух резисторов (делителя) R1 и Roc между выходом и инвертирующим входом, и соединив неинвертирующий вход ОУ с общей точкой, получим инвертирующий усилитель (рис. 6.4).
Рис. 6.4 Схема инвертирующего усилителя на ОУ
Зависимость выходного напряжения от входного сигнала (статическая амплитудная характеристика) такого усилителя рассчитывается по формуле:
где: R 1 и R ос – сопротивления, определяющие коэффициент усиления инвертирующего усилителя. Из формулы следует, что при значении R ос = R 1, амплитудная характеристика инвертирующего усилителя принимает следующий вид:
Модель инвертирующего усилителя в среде Multisim (рис. 6.5):
Рис. 6.5. Инвертирующий усилитель
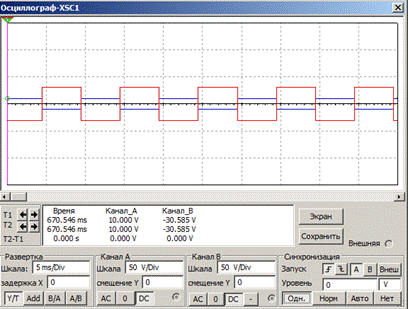
Рис. 6.6. Показания осциллографа, подключенного ко входу и выходу инвертирующего усилителя Неинвертирующий усилитель. Схема неинвертирующего усилителя представлена на рисунке 6.7.
Рис. 6.7. Схема неинвертирующего усилителя на ОУ.
Амплитудная характеристика неинвертирующего усилителя на ОУ рассчитывается по следующей зависимости:
где: R 1 и R ос – сопротивления, определяющие коэффициент усиления неинвертирующего усилителя. Из формулы следует, что при значении R ос = 0, амплитудная характеристика принимает следующий вид:
Модель инвертирующего усилителя в среде Multisim (рис. 6.8):
Рис. 6.8. Неинвертирующий усилитель
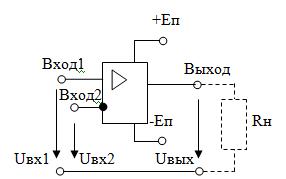
Рис. 6.9. Показания осциллографа, подключенного ко входу и выходу неинвертирующего усилителя Дифференциальный усилитель. Усиливает разность двух входных напряжений на соответствующих входах Uвх 1 и Uвх 2 и подавляет на них синфазный (одинаковый) сигнал помехи.
Рис. 6.10 Схема дифференциального усилителя на ОУ.
Амплитудная характеристика дифференциального усилителя на ОУ рассчитывается по следующей зависимости:
где: R 1 и R ос – сопротивления, определяющие коэффициент усиления дифференциального усилителя.
При этом должно соблюдаться условие:
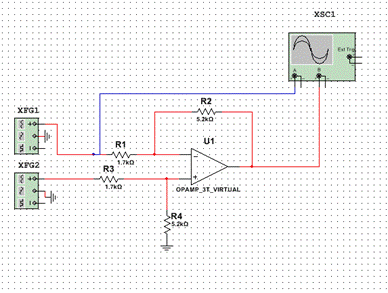
Модель инвертирующего усилителя в среде Multisim (рис. 6.11):
Рис. 6.11. Дифференциальный усилитель
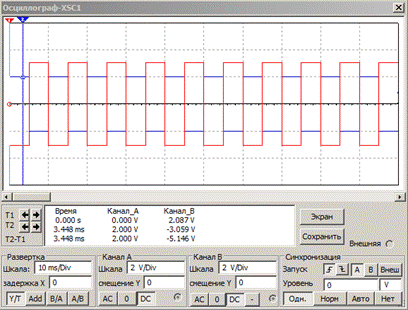
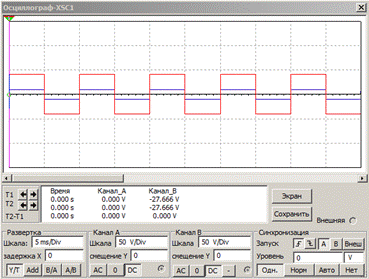
Рис. 6.11. Показания осциллографа, подключенного ко входу и выходу дифференциального усилителя
|


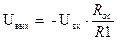 , (6.1)
, (6.1)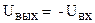 . (6.2)
. (6.2)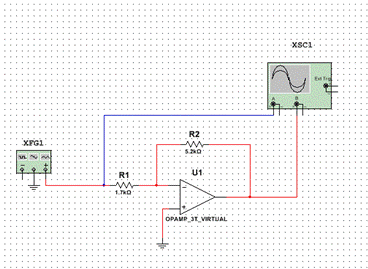
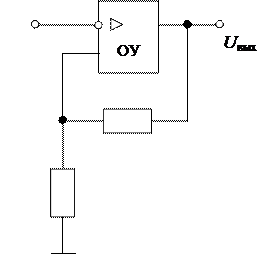
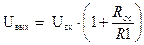 , (6.3)
, (6.3)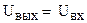 . (6.4)
. (6.4)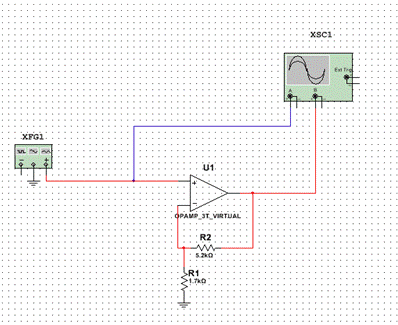

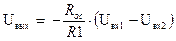 , (6.6)
, (6.6)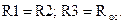 (6.7)
(6.7)