Показатели, характеризующие качество корреляционного уравнения
1. Коэффициент детерминации (R)2.
Выполняет двоякую роль: а) показывает вариацию результирующего признака за счет факторов, включенных в корреляционную модель; б) характеризует качество корреляционной модели, чем выше его значение, тем выше качество корреляционного уравнения. 0,8542=0,729=72,9% – качество уравнения высокое, правильно выбрана линейная форма связи. Реализации путевок по отелям на 72,9% зависит от стоимости основных фондов, а на 27,1% – от прочих факторов. 0,94512=0,893=89,3% – для многофакторной модели потребления мяса. Потребление мяса на 89,3% зависит от дохода на 1 члена семьи и числа членов семьи, а на 10,7% от прочих факторов. Модель высокого качества. 2. Критерий Фишера (F)
где R2 – коэффициент детерминации; т – число параметров уравнения регрессии; n – число единиц наблюдения. Если критерий ³3, то модель хорошего качества. Рассчитываем для парного линейного уравнения:
Высокое качество модели правильно отражает реальную действительность.
3. Критерий Стьюдента (txy)
где rxy – парный коэффициент корреляции; n – число единиц наблюдения. Критерий txy показывает статистическую значимость каждого фактора в модели. Если txy ³ 2, то фактор – статистически значимый для результативного показателя. txy=18,5. Для множественного уравнения (по мясу):
Уровень дохода на 1 члена семьи для многофакторного корреляционного уравнения, 4. Коэффициент эластичности
где а1 – параметр уравнения регрессии; Коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный показатель при изменении факторного на 1%. Для парного линейного уравнения:
С увеличением стоимости ОФ на 1% реализация путевок растет в среднем на 0,9697%. Коэффициент эластичности потребления мяса от дохода на 1 члена семьи:
С увеличением дохода на 1 члена семьи на 1% потребление мяса возрастает в среднем на 0,821%. Коэффициент эластичности потребления мяса от числа членов семьи:
С увеличением членов семьи на 1% потребление мяса уменьшается на 0,128%.
Контрольные вопросы и задания 1. В каких случаях переменные связаны корреляционной зависимостью? 2. Каковы задачи корреляционного анализа? 3. Укажите основные виды парной корреляционной зависимости и их уравнения. 4. Каков экономический смысл параметров уравнения а1 и а0 в уравнении линейной зависимости? 5. С помощью каких показателей характеризуют тесноту связи факторов? 6. В каких границах варьируют показатели оценки тесноты связи? 7. Для чего применяется коэффициент ассоциации? 8. Интерпретируйте тесноту связи по следующим коэффициентам корреляции: а) 0,95; б) 0,80; в) 0,43; г) 0,05. 9. Какая зависимость существует между парным коэффициентом корреляции и параметрами линейного уравнения? 10. Перечислите показатели оценки качества корреляционного уравнения. 11. Каковы условия хорошего качества корреляционной модели для критерия Фишера и Стьюдента? 12 Что показывают коэффициенты детерминации и эластичности?
8. РЯДЫ ДИНАМИКИ
|

 .
.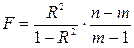 ,
,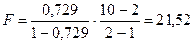 .
.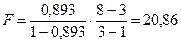 – тоже высокое качество.
– тоже высокое качество. ,
, – среднедушевой доход на 1 члена семьи – значимый фактор.
– среднедушевой доход на 1 члена семьи – значимый фактор.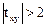 т.е. значимый фактор (число членов семьи).
т.е. значимый фактор (число членов семьи). ,
,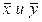 – средние значения факторного и результативного признака.
– средние значения факторного и результативного признака.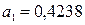 ;
;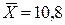 ;
;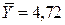 ;
;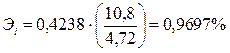 .
.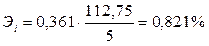 .
.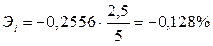 .
.


