Способы отбора
Репрезентативность выборки зависит не только от того, достаточно ли количество единиц отобрано, но и от того, каким способом они отбираются. Систему организации отбора единиц из генеральной совокупности называют способом отбора. В зависимости от того, участвует ли отобранная единица в дальнейшей выборке, различают повторный и бесповторный отбор. При повторном отборе однажды отобранная единица возвращается обратно в генеральную совокупность и снова участвует в выборке. При бесповторном отборе однажды отобранная единица обратно не возвращается. Ранее были приведены формулы расчета ошибок при повторном способе отбора. Ошибка бесповторного отбора равна соответствующей ошибке повторного, умноженной на коэффициент (К), который всегда меньше единицы:
Положим, что, соблюдая условия примера 2, производится не повторный, а бесповторный отбор, причем известно, что во всей партии 2000 изделий. Тогда предельная ошибка выборки составит:
Мы видим, что предельная ошибка выборки бесповторного отбора на 0,2% меньше ошибки повторного отбора, т.е. бесповторный отбор точнее повторного. Поправку на бесповторный отбор имеет смысл вводить, если доля выборки равна 10% и более. Необходимая численность бесповторной случайной выборки составит:
Положим, что соблюдая условия примера 3, производится не повторный, а бесповторный отбор, причем известно, что на предприятии 600 станков. Тогда необходимая численность выборки будет равна: станка, что на 61 станок меньше нежели при повторном способе отбора. Повторный и бесповторный отбор применяется в сочетании с разными способами отбора. В практической деятельности употребляется 5 способов отбора: случайный, механический, типический, групповой и комбинированный. Каждый способ отбора имеет свои особенности при проведении выборки и свои методы расчета средней ошибки. Собственно-случайным называется такой отбор, при котором единицы отбираются из всей генеральной совокупности на основе жеребьевки или по таблицам случайных чисел. Все приведенные ранее формулы расчета ошибок выборки относятся к собственно-случайному, отбору. Механический отбор заключается в отборе единиц из генеральной совокупности, производимом в каком-либо механическом порядке, например в отборе каждой пятой, каждой десятой и т.д. единицы, при определенном положении единиц в генеральной совокупности, например по алфавиту, Чаще всего механический отбор применяют там, где имеются элементы случайности в расположении материала. Поэтому средняя ошибка механической выборки определяется по формулам случайного отбора. Сущность группового (серийного) отбора заключается в том, что вместо случайного отбора единиц осуществляется отбор группами (сериями, гнездами). Внутри отобранных групп производится сплошное наблюдение. Применение серийной выборки обусловлено тем, что многие товары упаковываются в ящики, пачки и т.п. Поэтому при контроле качества упакованного товара рациональнее проверить несколько пачек (серий), чем из всех упаковок отбирать необходимое количество изделий. Поскольку внутри групп (серий) обследуются все единицы, средняя ошибка выборки зависит только от межгрупповой дисперсии или иначе дисперсии групповых средних. Серии могут быть равновеликими и неравновеликими. Межгрупповая дисперсия вычисляется по формулам: для средней количественного признака где
|

 .
.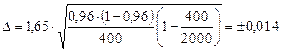 , или ±1,4%.
, или ±1,4%.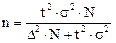 .
.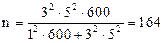
 ,
, – средняя в отдельных сериях;
– средняя в отдельных сериях; 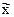 – общая средняя по всей выборочной совокупности; r – число отобранных серий;
– общая средняя по всей выборочной совокупности; r – число отобранных серий;


