Сущность и особенности выборочного исследования
Выборочным называется такое наблюдение, с помощью которого можно судить обо всей генеральной совокупности единиц на основе обследования только некоторой ее части, отобранной в случайном порядке. Выборочное исследование имеет ряд преимуществ перед сплошным, что открывает перед ним широкие возможности. На практике оно может использоваться самостоятельно для решения специальных задач, может занимать место сплошного наблюдения, либо применяться в сочетании со сплошным наблюдением. Различают генеральную совокупность, из которой производится отбор, и выборочную, которая отобрана из генеральной и подвергнута наблюдению. (Таблица 6.1)
Таблица 6.1 - Основные характеристики совокупностей, их обозначения и формулы
В результате случайного отбора выборочная характеристика может оказаться больше или меньше генеральной. Ошибкой выборки D (прописная буква греческого алфавита «дельта») называется разность соответствующих выборочных и генеральных характеристик:
Источниками этих расхождений являются ошибки регистрации индивидуальных величин и несплошной характер наблюдения. Последние называют иначе ошибками репрезентативности – представительства. Фактическую (предельную) ошибку выборки при собственно случайном повторном отборе определяют по формуле:
где t – число показывающее, сколько средних ошибок содержится в предельной ошибке (коэффициент доверия); µ (строчная буква греческого алфавита «мю») – средняя (стандартная) ошибка; s2– дисперсия; n – число отобранных единиц.
Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и отµносительная ошибка выборки:
В теории математической статистики доказывается, что возможные ошибки подчиняются закону нормального распределения, и что средняя или доля генеральной совокупности располагается в диапазонах средней ошибки выборки с вероятностью 0,683, Величина вероятности (Ф) вычисляется по интегралу вероятностей Лапласа. Ниже приводится выдержка из специальной таблицы для некоторых характерных значений t (Таблица 6.2). Таблица 6.2 – Величина вероятности
Пример 1. Найти с вероятностью 0,954 предельную ошибку выборочной средней и доверительные пределы среднего экзаменационного балла студентов вуза, если средний выборочный балл 100 студентов 4,05, а выборочная дисперсия успеваемости равна 0,36. Предельную ошибку Следовательно, предельная ошибка выборки: Генеральная средняя будет равна, а доверительные интервалы (пределы) генеральной средней исчисляем, исходя из двойного неравенства:
Таким образом, с вероятностью 0,954 можно утверждать, что средний экзаменационный балл студентов колеблется в пределах от 3,93 до 4,17. Пример 2. Найти с вероятностью 0,9 удельный вес стандартных изделий во всей партии, если среди обследуемых 400 изделий 384 оказались стандартными. Находим выборочную долю стандартных изделий:
и предельную ошибку доли
Следовательно, с вероятностью 0,9 (90%) можно утверждать, что генеральная доля стандартных изделий будет находиться в пределах При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки важно правильно определить численность (объем) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения. Путем несложного преобразования приведенных ранее формул можно получить формулы для определения необходимой численности (объема) выборки:
Пример 3. Какое количество станков необходимо обследовать, чтобы ошибка (D) среднего срока службы станка не превышала 1 года с вероятностью 0,997 (тогда t=3), если среднее квадратическое отклонение (s) срока службы станков равно 5 годам?
Величина коэффициента доверия t зависит от того, с какой вероятностью необходимо гарантировать пределы ошибки выборки. Эта величина диктуется существом дела. Если требуется, чтобы такая гарантия была дана с вероятностью 0,9, то из таблицы видно, что для этих условий t=1,65. Если достаточна вероятность 0,95, то t=1,96 и т.д. Пример 4. Какова вероятность того, что предельная ошибка выборочной средней продолжительности горения электрической лампочки не превысит 18 часов, при объеме выборки n=16 и s=24ч? Находим коэффициент доверия t:
|

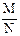











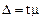 определяем по формуле повторного отбора, т.к. численность генеральной совокупности N неизвестна. Из представленных значений Ф(t) (см. табл.) для вероятности Ф=0,954 находим t=2.
определяем по формуле повторного отбора, т.к. численность генеральной совокупности N неизвестна. Из представленных значений Ф(t) (см. табл.) для вероятности Ф=0,954 находим t=2.



 , или ±1,16%.
, или ±1,16%. , или 96%±1,6%.
, или 96%±1,6%.
 станков.
станков. , следовательно, Ф(t)=0,997.
, следовательно, Ф(t)=0,997.


