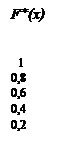Случайной величины
Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
Понятие плотность распределения вероятностей случайной величины Х для дискретной величины неприменима. Плотность распределения вероятностей f(x) – называют дифференциальной функцией распределения:
Свойство 1. Плотность распределения - величина неотрицательная:
Свойство 2. Несобственный интеграл от плотности распределения в пределах от
Пример 1.25. Дана функция распределения непрерывной случайной величины Х:
Найти плотность распределения f(x). Решение: Плотность распределения равна первой производной от функции распределения:
Задания для самостоятельной работы: 1. Дана функция распределения непрерывной случайной величины Х:
Найти плотность распределения. 2. Задана функция распределения непрерывной случайной величины Х:
Найти плотность распределения f(x). 1.3. Числовые характеристики непрерывной случайной величины
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством:
Предполагается, что интеграл сходится абсолютно. Частный случай. Если значения случайной величины принадлежат интервалу (a, b), то:
f(x) – плотность распределения случайной величины. Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси, определяется равенством:
Частный случай. Если значения случайной величины принадлежат интервалу (a, b), то:
Вероятность того, что непрерывная случайная величина Х примет значения, принадлежащие интервалу (a, b), определяется равенством:
Пример 1.26. Непрерывная случайная величина Х задана функцией распределения:
Найти математическое ожидание, дисперсию и вероятность попадание случайной величины Х в интервале (0; 0, 7). Решение: Случайная величина распределена на интервале (0, 1). Определим плотность распределения непрерывной случайной величины Х:
а) Математическое ожидание
б) Дисперсия
в)
Задания для самостоятельной работы: 1. Случайная величина Х задана функцией распределения:
Найти: а) математическое ожидание M(x); б) дисперсию D(x); в) определить вероятность попадания случайной величины Х в интервал (2, 3). 2. Случайная величина Х задана интегральной функцией распределения:
Найти: а) математическое ожидание M(x); б) дисперсию D(x); в) определить вероятность попадания случайной величины Х в интервал (1; 1, 5). 3. Случайная величина Х задана интегральной функцией распределения:
Найти: а) математическое ожидание M(x); б) дисперсию D(x); в) определить вероятность попадания случайной величины Х в интервал 1.4. Законы распределения непрерывной случайной величины 1.4.1. Равномерное распределение Непрерывная случайная величина Х имеет равномерное распределение на отрезке [ a, b ], если на этом отрезке плотность распределения вероятности случайной величины постоянна, а вне его равна нулю, т.е.:
Рис. 4.
Пример 1.27. Автобус некоторого маршрута движется равномерно с интервалом 5 минут. Найти вероятность того, что равномерно распределенная случайная величина Х – время ожидания автобуса составит менее 3 минут. Решение: Случайная величина Х – равномерно распределена на интервале [0; 5]. Плотность вероятности: Для того чтобы время ожидания не превысило 3 минут, пассажир должен появиться на остановке в интервале от 2 до 5 минут после ухода предыдущего автобуса, т.е. случайная величина Х должна попасть в интервал (2; 5). Т.о. искомая вероятность:
Задания для самостоятельной работы: 1. а) найти математическое ожидание случайной величины Х распределенной равномерно в интервале (2; 8); б) найти дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной равномерно в интервале (2; 8). 2. Минутная стрелка электрических часов перемещается скачком в конце каждом минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 секунд. 1.4.2. Показательное (экспоненциальное) распределение Непрерывная случайная величина Х распределена по показательному закону, если ее плотность вероятности имеет вид:
где
Таким образом
Рис. 5.
Числовые характеристики:
Пример 1.28. Случайная величина Х – время работы электролампочки - имеет показательное распределение. Определить вероятность того, что время работы лампочки будет не меньше 600 часов, если среднее время работы - 400 часов. Решение: По условию задачи математическое ожидание случайной величины Х равно 400 часам, следовательно:
Искомая вероятность
Окончательно: Задания для самостоятельной работы: 1. Написать плотность и функцию распределения показательного закона, если параметр 2. Случайная величина Х задана функцией распределения вероятностей:
Найти математическое ожидание и дисперсию величины Х. 3. Случайная величина Х задана функцией распределения вероятностей:
Найти математическое ожидание и среднее квадратическое отклонение случайной величины. 1.4.3. Нормальное распределение Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид:
где а – математическое ожидание, Вероятность того, что Х примет значение, принадлежащее интервалу
Распределение, у которого
Рис. 6. Вероятность того, что абсолютная величина отклонена меньше положительного числа
В частности, при а= 0 справедливо равенство:
Пример 1.29. Случайная величина Х распределена нормально. Среднее квадратическое отклонение Решение: Задания для самостоятельной работы: 1. Написать плотность вероятности нормального распределения случайной величины Х, зная, что M(x)= 3, D(x)= 16.
2. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (15; 20).
3. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением
4. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением
Раздел II. Элементы математической статистики 2.1. Функция распределения. Полигон и гистограмма частот
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения Х относительную частоту события Х=x:
где nx – число вариант, меньших Х; n – объем выборки. Свойства эмпирической функции: Свойство 1. Значение эмпирической функции принадлежит отрезку [0; 1]. Свойство 2. F*(x) – неубывающая функция. Свойство 3. Если xi – наименьшая варианта, а Xk – наибольшая, то F*(x)= 0 при Пример 2.1. Найти эмпирическую функцию по данному распределению выборки:
Решение: 1. Найдем объем выборки n= 10 + 15 + 25 = 50. 2. На основании свойств функции хмин= 1, т.о. при 3. При
4. При
5. Так как хмакс= 6, то при x> 6 F*(x)= 1. 6. Искомая функция:
График этой функции изображен на рис. 7.
Рис. 7.
Задания для самостоятельной работы: 1. Найти эмпирическую функцию по данному распределению выборки: а)
б)
2. Найти эмпирическую функцию по данному распределению выборки: а)
б)
|




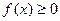
 до
до  равен единице:
равен единице:







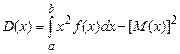
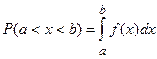 .
.

 :
:



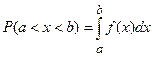




 .
.







 ;
;  ;
;  .
.
 .
.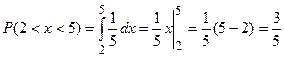

 – параметр показательного распределения.
– параметр показательного распределения.


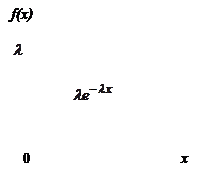


 ;
;  ;
;  ;
;  .
. ;
; 
 , где
, где ;
;
 .
.


 – среднее квадратическое отклонение Х.
– среднее квадратическое отклонение Х. :
: , где
, где – функция Лапласа.
– функция Лапласа. ;
;  , т.е. с плотностью вероятности
, т.е. с плотностью вероятности  называется стандартным.
называется стандартным.
 :
: .
.
 . Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине будет меньше 0, 3.
. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине будет меньше 0, 3. .
.

 мм и математическим ожиданием а= 0. Найти вероятность того, что из 3 независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.
мм и математическим ожиданием а= 0. Найти вероятность того, что из 3 независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.


 и F*(x)= 1 при
и F*(x)= 1 при  .
.
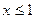 F*(x)= 0.
F*(x)= 0. значение функции х= 1 наблюдалось 10 раз, следовательно:
значение функции х= 1 наблюдалось 10 раз, следовательно:
 значение х= 1 и х= 4 наблюдалось n1+n4= 10 + 15 = 25, следовательно:
значение х= 1 и х= 4 наблюдалось n1+n4= 10 + 15 = 25, следовательно: