Условные средние
Условной средней Например: при Условным средним Условным математическим ожиданием дискретной случайной величины
Условное математическое ожидание есть функция от х Аналогично определяется условное математическое ожидание Условное математическое ожидание Это уравнение называют выборочным уравнением выборочной регрессии Аналогично уравнение При определенной корреляционной зависимости решаются две основные задачи: Первая задача теории корреляции – устанавливает форму корреляционной зависимости, т.е. вид функции регрессии: линейная или нелинейная. Вторая задача теории корреляции – оценить тесноту (силу) корреляционной связи (она оценивается по величине рассеяния у вокруг условного среднего Уравнение линейной корреляции можно записать в виде уравнения прямой линии:
Угловой коэффициент прямой линии регрессии
Выборочные уравнения прямой линии среднеквадратичной регрессии по несгруппированным данным имеют вид:
где Пример 2.14. Найти выборочное уравнение прямой линии регрессии
Для определения параметров выборочного уравнения составим таблицу:
Задания для самостоятельной работы: 1. На основании полученных измерений величин X и Y:
Найти линейную регрессию Y на X и выборочный коэффициент корреляции. 2. На основании полученных по результатам измерений значений величин X и Y:
Найти линейную регрессию X и Y и выборочный коэффициент корреляции. 3. В магазине постельных принадлежностей были проверены в течение пяти дней подсчеты числа покупок простыней X и подушек Y:
Найти выборочное уравнение линейной регрессии Y на X и выборочный коэффициент корреляции. 2.5.2. Корреляционная таблица При большом числе наблюдений одного и того же значения х может встретиться
|

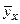 называют среднее арифметическое наблюдаемых значений
называют среднее арифметическое наблюдаемых значений 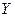 , соответствующих
, соответствующих 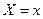 .
.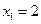 величина
величина 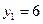 ;
; 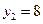 ;
; 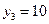 . Условная средняя
. Условная средняя 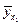 определяется выражением
определяется выражением 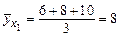 .
. называется среднее арифметическое наблюдаемых значений Х, соответствующих
называется среднее арифметическое наблюдаемых значений Х, соответствующих  .
.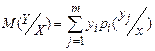
 ;
; 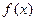 - называют функцией регрессии
- называют функцией регрессии 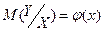 .
.  - функция регрессии.
- функция регрессии. есть функция от х, следовательно, его оценка, т.е. условное среднее
есть функция от х, следовательно, его оценка, т.е. условное среднее  - тоже функция от х, обозначив эту функцию через
- тоже функция от х, обозначив эту функцию через 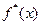 , получим уравнение
, получим уравнение 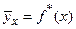 .
.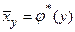 называют уравнением регрессии Х на
называют уравнением регрессии Х на 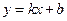 .
.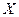 называют выборочным коэффициентом регрессии
называют выборочным коэффициентом регрессии  . Он является оценкой коэффициента регрессии
. Он является оценкой коэффициента регрессии 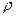
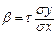 .
.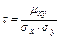 - коэффициент корреляции
- коэффициент корреляции 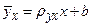 ,
,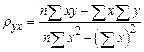 ;
; 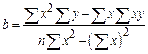 .
. наблюдений:
наблюдений: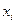
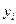
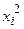
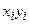
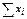



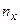 раз, одно и то же значение y -
раз, одно и то же значение y - 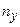 раз, одна и та же пара чисел (x, y) может наблюдаться
раз, одна и та же пара чисел (x, y) может наблюдаться  . Поэтому данные наблюдений группируют, т.е. подсчитывают частоты
. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты 


