Среднее квадратическое отклонениеДля удобства оценки рассеяния возможных значений случайной величины вокруг ее среднего значения вводят понятие среднего квадратического отклонения:
Размерность Свойства дисперсии квадратического отклонения такие же, как и у дисперсии. Задания для самостоятельной работы: 1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной законом распределения: а)
б)
2. Случайные величины X и Y независимы. Найти дисперсию случайной величины 3. Найти математическое ожидание случайной величины Z, если известны математические ожидания X и Y: а) б) 4. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:
5. Найти дисперсию дискретной случайной величины Х – числа отказа элементов некоторого устройства в 10 независимых опытах, если вероятность отказа элемента в каждом опыте равна 0, 9. 1.2.2. Закон больших чисел При определенных сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным. Эти условия указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим.
|
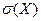совпадает с размерностью случайной величины Х. 
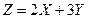, если известно, что D(X)= 5; D(Y)= 6.
, M(X)= 3; M(Y)= 6.
