Классическое определение вероятности. Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех простых
Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех простых, попарно несовместных, единственно возможных и равновозможных исходов испытания:
Возможны случаи: 1. 2. 3. Вероятность события есть неотрицательное число из интервала [0, 1]
Пример 1.1. В урне находятся 12 белых и 6 красных шаров. Какова вероятность того, что наудачу вынутый шар будет белым? Решение: Пусть A - событие, состоящее в том, что вынутый шар белый.
Следовательно, по формуле
Пример 1.2. При перевозке ящика, в котором содержались 31 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно, какая. После перевозки наудачу извлечена одна деталь, она оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь. Решение: а) извлеченная стандартная деталь, очевидно, не могла быть утеряна, могла быть потеряна любая из остальных деталей n= (31-1+10)=40; среди них стандартных m= (31-1)=30; Таким образом, б) среди n= 40 деталей, каждая из которых могла быть утеряна, было 10 нестандартных, т.е. m= 10, тогда Задания для самостоятельной работы: 1. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 5. 2. Найти вероятность того, что в наудачу написанном двузначном числе цифры разные. 3. Набирая номер телефона, абонент забыл две последние цифры и набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
В задачах на классическое определение вероятности для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов используются формулы комбинаторики. 1. Размещения, если комбинации отличаются не только составом элементов, но и порядком их следования. Их число находится по формуле:
2. Сочетания – это комбинации, которые отличаются друг от друга хотя бы одним элементом. Их число определяется по формуле:
3. Перестановки – это комбинации из n элементов по n, которые отличаются только порядком расположения элементов. Их число определяется по формуле:
4. Если при выборе m элементов из n элементы возвращаются обратно и упорядочиваются, то говорят, что это размещение с повторениями. Их число
Пример 1.3. В группе студентов 10 учебных предметов и 5 различных занятий в день. Сколькими способами могут быть распределены занятия в один день? Решение: n= 10; m= 5 Пример 1.4. В группе 25 студентов. На профсоюзное собрание выбирают делегацию из 3 человек. Сколькими способами может быть выбрана эта тройка? Решение: Пример 1.5. Сколькими способами можно разместить 6 человек за столом, на котором поставлено 6 приборов. Решение: Пример 1.6. Сколько пятизначных чисел можно составить, используя цифры: а) 2, 5, 7, 8 б) 0, 1, 9? Решение: а) б) если пятизначное число состоит из цифр 0, 1, 9, то первую цифру можно выбирать двумя способами, каждую из оставшихся можно выбирать тремя способами. Согласно правилу вычисления можно записать:
или
|



 - вероятность достоверного события;
- вероятность достоверного события; - вероятность невозможного события;
- вероятность невозможного события; - вероятность случайного события.
- вероятность случайного события. .
. =12+6=18 - число всех равновозможных исходов опыта;
=12+6=18 - число всех равновозможных исходов опыта; =12 – число исходов, благоприятствующих событию
=12 – число исходов, благоприятствующих событию 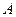 .
.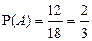 .
. ;
; .
.

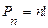
 вычисляется по формуле:
вычисляется по формуле:
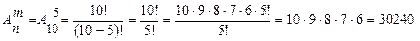




 ;
; ,
,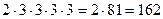 .
.


