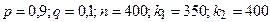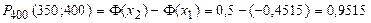Интегральная теорема Лапласа
Вероятность
При пользовании таблицей учитывают свойства функции 1. Функция 2. Для значений Значения x1 и x2 определяются соотношением:
Интегральную и локальную теоремы Лапласа применяют в задачах, где n достаточно велико. Пример 1.18. Всхожесть семян оценивается вероятностью 0, 9. Найти вероятность того, что из 400 посеянных семян взойдут 350. Решение: Имеем Согласно локальной теореме Лапласа можно записать:
Определим
По таблице Приложения 1 Т.о. Пример 1.19. Всхожесть семян оценивается вероятностью 0, 9. Найти вероятность того, что из 400 семян взойдут не менее 350. Решение:
Задания для самостоятельной работы: 1. Отдел технического контроля проверяет партию из 10 деталей. Вероятность того, что деталь стандартная, равна 0, 75. Найти наивероятнейшее число деталей, которые будут признаны стандартными. 2. Вероятность появления события в каждом из независимых испытаний равна 0, 3. Найти число испытаний n, при котором наивероятнейшее число появлений события в этих испытаниях будет равна 30. 3. В семье 5 детей. Найти вероятность того, что среди детей: 1) 2 мальчика; 2) не более 2 мальчиков. Вероятность рождения мальчика принимается 0, 5. 4. В магазин вошли 5 покупателей. Найти вероятность того, что не менее 3 из них совершат покупки, если вероятность совершить покупку для каждого вошедшего одна и та же и равна 0, 3. 5. Вероятность того, что покупателю потребуется костюм 50 размера, равна 0, 2. Найти вероятность того, что среди 100 покупателей потребуют костюм 50 размера 25 человек. 6. Вероятность рождения мальчика примем равной 0, 5. Найти вероятность того, что среди 400 новорожденных детей будут 200 мальчиков. 7. В среднем левши составляют 1%. Какова вероятность того, что среди 1100 студентов не менее 20 левшей? 8. Было посажено 400 деревьев. Найти вероятность того, что число привившихся деревьев больше 250, если вероятность того, что отдельное дерево приживается, равна 0, 8.
1.2. Случайные величины Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Различают случайные величины: Дискретные (прерывные) случайные величины, которые принимают отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Непрерывной называют случайную величину, возможные значения которой сплошь заполняют некоторый промежуток, конечный или бесконечный. Число возможных значений непрерывной случайной величины бесконечно. 1.2.1. Числовые характеристики дискретных случайных величин
Числовые характеристики случайной величины описывают случайную величину суммарно; к ним относят математическое ожидание, дисперсию и среднее квадратическое отклонение.
|

 того, что событие А появится в n испытаниях не менее k1 и не более k2 раз, приближенно равна:
того, что событие А появится в n испытаниях не менее k1 и не более k2 раз, приближенно равна: , где
, где  – функция Лапласа, значения которых занесены в таблицу.
– функция Лапласа, значения которых занесены в таблицу. :
: .
. приближенно можно считать
приближенно можно считать  .
.
 .
. ;
; 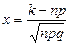 ;
; 


 .
. .
.