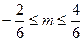Вычисление вероятностей
Пример 1.7. В ящике 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что среди извлеченных деталей две будут окрашены. Решение: Пусть событие А – среди извлеченных 4 деталей 2 окрашены
По формуле Пример 1.8. В группе 25 студентов, среди которых 8 отличников. По списку наудачу отобрано 9 студентов. Найти вероятность того, что среди отобранных студентов - 5 отличников. Решение: Пусть событие А – среди 9 отобранных студентов 5 отличников.
По формуле:
Задания для самостоятельной работы: 1. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает 3 вопроса, предложенных ему экзаменатором:
2. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранных билета окажутся выигрышными:
3. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков:
4. В замке на общей оси 5 дисков. Каждый диск разделен на 6 секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть:
1.1.2. Теоремы сложения и умножения вероятностей
Теорема сложения вероятностей несовместных событий: Вероятность появления одного из двух несовместных событий, безразлично, какого, равна сумме вероятностей этих событий:
Теорема сложения вероятностей совместных событий: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B)= P(A)+P(B)-P(AB) Теорема умножения вероятностей: Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предложении, что первое событие уже наступило:
Пример 1.9. Студент сдает экзамен по теории вероятностей. Вероятность получить на экзамене «2» равна 0, 1; «3» – 0, 6; «4» – 0, 2; «5» – 0, 1. Какова вероятность того, что студент получит на экзамене положительную оценку? Решение: Пусть событие А – студент получит на экзамене положительную оценку. Задачу можно решить двумя способами. Первый способ.
Второй способ.
Пример 1.10. В урне находятся 7 белых и 3 черных шара. Подряд извлекают 2 шара. Какова вероятность того, что оба они черные? Решение: Первый способ: пусть событие А – первый шар черный, событие В – второй шар черный.
Второй способ: Пример 1.11. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки? Решение: Пусть событие А – появление шестерки на первой кости, В – на второй. Тогда (А+В) – появление хотя бы одной шестерки при бросании костей. События А и В совместные. По формуле
Задания для самостоятельной работы: 1. В группе из 25 студентов, среди которых 10 девушек, разыгрывают 5 билетов. Определить вероятность того, что среди обладателей билетов окажутся 2 девушки.
2. В партии из 15 однотипных стиральных машин 5 машин изготовлены на заводе А, а 10 – на заводе В. Случайным образом отобрано 5 машин. Найти вероятность того, что 2 из них изготовлены на заводе А.
3. В порт приходят корабли только из трех пунктов отправления. Вероятность появления корабля из первого пункта равна 0, 2, из второго пункта – 0, 6. Найти вероятность прибытия корабля из третьего пункта.
Вероятность появления хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Пример 1.12. Вероятности попадания в цель при стрельбе из трех орудий таковы: Решение. События А1, А2 и А3 – попадание первого орудия, второго и третьего – независимы в совокупности. Определим вероятности противоположных событий
Искомая вероятность
Задания для самостоятельной работы: 1. В студии телевидения 3 телевизионные камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна р= 0, 6. Найти вероятность того, что в данный момент включена хотя бы одна камера (событие А).
2. Вероятность того, что событие А появится хотя бы один раз при двух независимых испытаниях, равна 0, 75. Найти вероятность появления события в одном испытании (в предположении, что вероятность появления события в обоих испытаниях одна и та же).
1.1.3. Формула полной вероятности. Вероятность гипотез. Формула Байеса Вероятность события А, которая наступит лишь при условии появления одного из несовместных событий В1, В2,..., Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
Пример 1.13. В сборочный цех завода поступают 40% деталей из I цеха и 60% - из II цеха. В I цехе производится 90% стандартных деталей, а во II – 95%. Найти вероятность того, что наудачу взятая сборщиком деталь окажется стандартной. Решение: Событие А – взятая наудачу деталь стандартная. Возможны две гипотезы H1 – деталь изготовлена цехом I. H2 - II цехом. События H1 и H2 – образуют полную группу
По формуле полной вероятности
Решение задачи можно представить схематически:
Пример 1.14. В примере 1.13. «Наудачу взятая деталь оказалась стандартной» (Это ключевая фраза, она всегда есть в задачах с применением формулы Бейеса). Найти вероятность того, что деталь изготовлена I цехом. По формуле Бейеса Р(А) – определяется по формуле полной вероятности
Примечание: до испытания H1=0, 4, после испытания H1=0, 39. Задания для самостоятельной работы: 1. Прибор содержит 2 микросхемы. Вероятность выхода из строя в течение 10 лет первой микросхемы равна 0, 07, а второй – 0, 10. Известно, что из строя вышла первая микросхема.
2. Электролампы изготавливаются на трех заводах. Первый завод производит 45% общего количества электроламп, второй – 40%, третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%, третьего – 81%. В магазин поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине лампа окажется стандартной?
3. Завод выпускает три типа предохранителей для магнитофона. Доля каждого из них в общем объеме составляет: 30%; 50% и 20% соответственно. При перегрузке сети предохранитель первого типа срабатывает с вероятностью 0, 8; второго – 0, 9; третьего – 0, 85. Выбранный произвольно предохранитель не сработал при перегрузке сети. Какова вероятность того, что он принадлежал к первому типу?
4. В группе спортсменов 15 лыжников, 5 велосипедистов и 10 бегунов. Вероятность выполнить квалификационную норму такова: для лыжника - 0, 8, для велосипедиста – 0, 7, для бегуна – 0, 6. Выбранный наудачу спортсмен выполнил норму. Найти вероятность того, что это был бегун.
5. Турист может пообедать в 3 столовых города. Вероятность того, что он отправится в первую столовую -
1.1.4. Повторение испытаний. Формула Бернулли Вероятность того, что в результате проведения n одинаковых независимых испытаний, некоторое событие А наступит m раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью, Р(А)=р определяется по формуле Бернулли:
Пример 1.15. Игральный кубик бросается 3 раза. Найти вероятность того, что шестерка выпадет: а) 2 раза; б) 3 раза; в) ни разу. Решение: а) б) в) Наивероятнейшее число m0 появления события А в n независимых испытаниях по формуле:
1. Если числа 2. Если же числа Пример 1.16. Три раза подбросили монету. Найти наивероятнейшее число появлений герба и построить многоугольник распределения вероятностей появления герба. Решение:
Следовательно, герб появится либо один раз, либо два раза. Построим многоугольник распределения вероятностей. Для этого найдем вероятности следующих событий: а) герб не появится ни разу при 3 бросаниях
б) герб появится один раз в) герб появится два раза г) герб появится три раза Многоугольник распределения вероятностей появления герба при трех бросаниях изображен на рис. 1.
Рис.1. mi – число выпадений герба Пример 1.17. Игральная кость бросается три раза. Найти наивероятнейшее число появлений шестерки и построить многоугольник распределения вероятностей появления шестерки. Решение:
Следовательно, вероятнее всего шестерка не появится ни разу. Построим многоугольник распределения вероятностей появления шестерки: а) шестерка не появится ни разу при трех бросаниях:
б) шестерка появится один раз:
в) шестерка появится два раза:
г) шестерка появится три раза:
Многоугольник распределения вероятностей появления шестерки при трех бросаниях игральной кости изображен на рис. 2.
Рис. 2. mi – число выпадений шестерки.
|


 – общее число четверок, которые можно сформировать из 15 деталей
– общее число четверок, которые можно сформировать из 15 деталей – число четверок, благоприятствующих событию А.
– число четверок, благоприятствующих событию А.

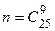 – общее число «девяток», которые можно отобрать из 25 студентов;
– общее число «девяток», которые можно отобрать из 25 студентов; – число «девяток», благоприятствующих событию А.
– число «девяток», благоприятствующих событию А.

 .
.




 ;
; 
 , здесь Р (3) – вероятность получить на экзамене оценку «3» и т.д.
, здесь Р (3) – вероятность получить на экзамене оценку «3» и т.д.
 , т.к. событие А и событие «2» - получить двойку на экзамене - являются противоположными.
, т.к. событие А и событие «2» - получить двойку на экзамене - являются противоположными.


 находим
находим


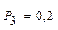
 :
:
 . Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. :
: ;
;  ;
; 


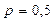

 – формула полной вероятности
– формула полной вероятности – формулы Бейеса
– формулы Бейеса ;
;  .
. 
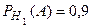 – условная вероятность события А при условии гипотезы H1
– условная вероятность события А при условии гипотезы H1 – условная вероятность события А при условии гипотезы H2
– условная вероятность события А при условии гипотезы H2
 .
.


 А
А






 , во вторую -
, во вторую - 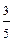 и в третью –
и в третью –  ; вторая -
; вторая -  . Турист пришел в одну из столовых и пообедал. Какова вероятность того, что он направился во вторую столовую.
. Турист пришел в одну из столовых и пообедал. Какова вероятность того, что он направился во вторую столовую.
 , где
, где  – вероятность ненаступления данного события А (она тоже постоянна).
– вероятность ненаступления данного события А (она тоже постоянна).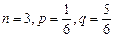
 ;
;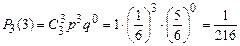 ;
; .
.
 и
и  – дробные, то число m0 – единственное.
– дробные, то число m0 – единственное.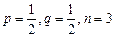
 ;
;  . Т.о.
. Т.о. 
 ;
; ;
;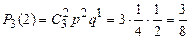 ;
; .
.


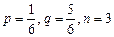
 ;
;  . Т.о.
. Т.о.