Математическое ожиданиеМатематическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности:
Пример 1.20. Найти математическое ожидание случайной величины X, зная закон ее распределения:
Решение: Вероятностный смысл полученного результата таков: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины. Свойства математического ожидания: 1. 2. 3. 4. 5. Математическое ожидание М(Х) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
|
, С – постоянная величина.
.
.
.
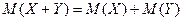