Непрерывное распределение признака Х
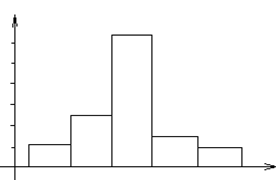
При непрерывном распределении признакаХ весь интервал, в котором заключены наблюдаемые значения признака, разбивают на ряд частичных интервалов длиной h и находят ni – сумму частот вариант, попавших в i -й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению Площадь частичного интервала равна Площадь гистограммы частот численно равна сумме всех частот, т.е. объему выборки Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению
Пример 2.2. Построить полигон частот по данному распределению выборки:
Решение: 1. Отложим на оси абсцисс варианты xi, а на оси ординат соответствующие им частоты ni. 2. Соединив точки (xi; ni) отрезками прямых, получим искомый полигон частот (рис. 8).
Рис. 8. Задания для самостоятельной работы: 1. Построить полигон частот по данному распределению выборки: а)
б)
2. Построить полигон относительных частот по данному распределению выборки: а)
б)
Пример 2.3. Построить гистограмму частот по данному распределению выборки объема n= 100:
Решение: 1. Для каждого интервала находим плотность частоты 2. Построим на оси абсцисс заданные интервалы hi= 4. На каждом интервале проводим параллельные отрезки, соответствующие плотностям частоты
Рис. 9. Пример 2.4. Построить гистограмму относительных частот по данному распределению выборки:
Решение: 1. Определим объем выборки:
2. Найдем соответствующие относительные частоты:
3. Найдем плотности относительных частот для каждого интервала 4. Строим гистограмму относительных частот:
Рис. 10.
Задания для самостоятельной работы: 1. Построить гистограмму частот по данному распределению выборки:
а)
б)
2. Построить гистограмму относительных частот по данному распределению выборки: а)
б)
2.2. Статистические оценки параметров распределения Статистической оценкой Статистические оценки различают: · точечные; · интервальные. Точечной называют оценку, которая определяется одним числом Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки (отсутствует систематическая ошибка). Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру (имеется систематическая ошибка). Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя
где xi – варианта выборки; ni – частота варианты xi; Смещенной оценкой генеральной дисперсии служит выборочная дисперсия:
Для вычисления дисперсии используют более удобную формулу:
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:
Несмещенная оценка должна быть эффективной и состоятельной.
|

 (плотность частоты).
(плотность частоты). – сумме частот, попавших в i -й интервал.
– сумме частот, попавших в i -й интервал. .
. (плотность относительной частоты).
(плотность относительной частоты). ;
;  – относительная частота вариант, попавших в i -й интервал.
– относительная частота вариант, попавших в i -й интервал.



 i
i
 и записываем в таблицу.
и записываем в таблицу. . По данным из таблицы строим гистограмму частот (рис. 9).
. По данным из таблицы строим гистограмму частот (рис. 9).

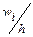
 .
.
 ;
;  ;
;  ;
;  .
. ; h= 2;
; h= 2;  ;
;  ;
;  .
.


 неизвестного параметра
неизвестного параметра  теоретического распределения называют функцию
теоретического распределения называют функцию  от наблюдаемых случайных величин
от наблюдаемых случайных величин  .
.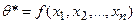 , где
, где  :
: ,
, – объем выборки.
– объем выборки. .
. .
.



